6. DM HALO PROFILES

In this section, we will introduce the DM halo profiles that are presently adopted: the empirical ones and those emerging from specific theoretical scenarios, see Fig. 7. It is useful to remind that M_h(r) = G⁻¹ V_h²(r) r = ∫₀^r 4π r² ρ_h(r) dr with V_h(r) the halo contribution to the circular velocity V(R).

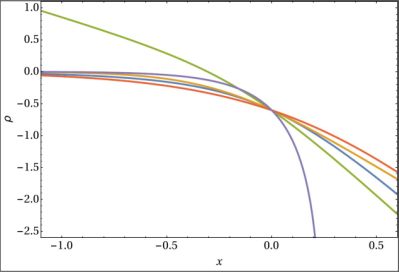Figure 7. DM halos density profiles. NFW (green), Burkert-URC (blu), fully degenerate fermionic particles (violet), Pseudo Isothermal (yellow) and Binney-URC (red).

The empirical DM halo density profile, adopted for the URC of Persic, Salucci and Stel (1996), takes the form (see also Binney and Tremaine 2008)

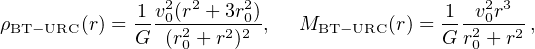(29)

where r₀ and v₀ are the core radius and the asymptotic circular velocity of the halo, respectively.

Navarro–Frenk–White

In ΛCDM the structure of virialized DM halos, obtained by N-body simulations, have a universal spherically averaged density profile, ρ_NFW (r) (Navarro et al. 1997):

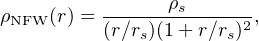(30)

where ρ_s and r_s are strongly correlated: r_s ≃ 8.8 (M_vir / 10¹¹ M_⊙)^0.46 kpc (e.g., Wechsler et al. 2006). We define X ≡ r / R_vir, the concentration parameter c ≡ r_s / R_vie is a weak function of mass (Klypin et al. 2010):

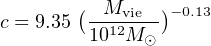(31)

but a very important quantity in determining the density shape at intermediate radii. The circular velocity for an NFW dark matter halo is given by

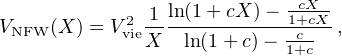(32)

with M_vir = 100 4/3π ρ_c R_vir³ and ρ_c = 1.0 × 10⁻²⁹ g/cm³.

Burkert-URC

The Burkert empirical profile (Burkert 1995, Salucci and Burkert 2000) well reproduces, in cooperation with the velocity components of the stellar and gaseous disks, the individual circular velocities of spirals, dwarf disks and low surface brightness systems. Furthermore, this profile is at the basis of the universal rotation curve of the above systems. The density profile reads as

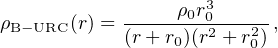(33)

r₀ and ρ₀ are the core radius and central density respectively. The velocity profile is:

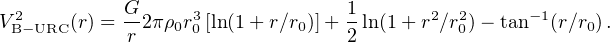(34)

This profile represents the (empirical) family of cored distributions (see Fig. 7). To discriminate among them the correct one is, currently, very difficult. It would require a large number of accurate measurements of RCs at inner radii r < r₀.

Pseudo-isothermal profile

The PI halo profile ρ_PI(r) = ρ₀ r₀² / (r² + r₀²) is an alternative cored distribution to Eq. (34). This density profile implies that V_PI(r) = const for r ≫ R_opt, which disagrees with the RC profiles at very outer radii that show a decline with radius (Salucci et al. 2007).

Fermionic halos

In this scenario there is a strong degeneracy limit for which the DM particles velocity dispersion σ_{DM, min}²(ρ) has the minimal value. This represents the most compact configuration for a self-gravitating fermionic halo (see e.g., Di Paolo et al. 2018). The density profiles of such fully degenerate halos are universal, depending only on the mass of the configuration:

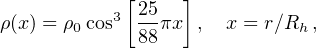(35)

where ρ₀ is the central DM halo density. This profile is quite peculiar and recognizable in the RCs.

Zhao halos

The following density profile (Zhao 1996):

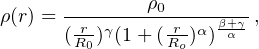(36)

where ρ₀ is the central density and R₀ the “core radius”, that, initially, was not proposed for the DM halo density, is defined by the set of parameters: α, β, γ. The case (1, 3, γ) is sometimes used as a “cored-NFW” profile. This is incorrect because both in the Burkert and in the NFW profiles, the inner regions are not related with the outermost regions, as, instead occurs in the Zhao model. Moreover, with the latter, we pass from the two free parameters of most of the halo models in the ballpark, to the five of Eq. (36). This seems in disagreement with observations in spirals, ellipticals and spheroidals that suggest that DM halos are one (two)-parameters family.

Transformed halos

We want to draw the attention on the profiles which are the outcome of the primordial NFW halos after that these have experienced the effects that it is called baryonic feedback (e.g., Di Cintio et al. 2014). They seem in agreement with those observed around galaxies. However, the collisionless DM paradigm requires that such kind of transformation has occurred in every galaxy of any luminosity and Hubble type and to reach this goal seems extremely difficult. On the other side, the effect of the baryonic feedback to DM halos has to be investigated, no matter what the nature of DM is. In conclusion, a review on this crucial complex and still on its infancy issue must be a goal future work.