3.2. The effects on the expansion and cooling rates of the Universe

In the previous section we discussed how the presence of strong magnetic fields affects the rates of the weak reactions which are responsible for the chemical equilibrium of neutrons and protons before BBN. The knowledge of such rates is, however, not sufficient to predict the relic abundances of the elements synthesized during BBN. In fact, the temperature T_F at which (n / p)_eq is frozen is determined by the competition of the weak reaction and the Universe expansion according to the condition

(3.19)

From this expression it is clear that in order to determine T_F the knowledge of the Universe expansion rate H(T) is also required.

In the absence of a cosmological term and assuming the effect of the magnetic field on the Universe geometry to be negligible, H is determined by

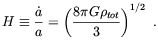
(3.20)

where, according to the standard notation, a is the scale factor of the Universe, G the Newton gravitational constant and (T) is the energy density of the Universe. In the presence of a magnetic field

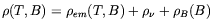
(3.21)

where _em(T, B) is the energy density of the standard electromagnetic component (photons + electrons and positrons) of the heat-bath and is the energy density of all neutrino species (the reason why _em depends on the magnetic field strength will be discussed in the next section). We see that to the standard components of it adds now the contributions of the magnetic field energy density

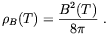
(3.22)

It is worthwhile to observe that, concerning its direct contribution to , the magnetic field behaves like any relativistic component of the heat-bath. In fact, by assuming that the field is not too tangled on scales smaller than the magnetic dissipation scale, and that the Universe geometry is not affected by the magnetic field (see Sec. 2.1), the magnetic flux conservation during the Universe expansion implies

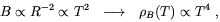
(3.23)

which is the same behaviour of the radiation.

In the absence of other effects, the relation (3.23) would allow to parametrize the effect of the magnetic field in terms of a correction to the effective number of massless neutrino species N^B [98]. Indeed, by comparing the contribution of N light (m << 1 MeV) neutrino species with the energy density of the Universe, which is

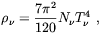
(3.24)

with (3.22) one gets

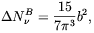
(3.25)

where b B / T².

Before closing this section we have to mention another possible consequence of the faster Universe expansion induced by the presence of the magnetic field. The effect is due to shortening of time between weak reactions freeze-out and breaking of the deuterium bottleneck. It follows that neutrons have less time to decay before their confinement into nucleons take place which turns into a larger abundance of ⁴He. In Ref. [98] it was showed that such an effect is generally sub-dominant.