


A. The issues for observational cosmology
We have to make two points. First, cosmology has a substantial observational and experimental basis that shows many aspects of the standard model almost certainly are good approximations to reality. Second, the empirical basis is not nearly as strong as it is for the standard model for particle physics: in cosmology it is not yet a matter of measuring the parameters in a well-established theory.
To explain the second point we must remind those more accustomed to experiments in the laboratory than observations in astronomy of the astronomers' tantalus principle: one can look at distant objects but never touch them. For example, the observations of supernovae in distant galaxies offer evidence for the detection of dark energy, under the assumption that distant and nearby supernovae are drawn from the same statistical sample (that is, that they are statistically similar enough for the purpose of this test). There is no direct way to check this, and it is easy to imagine differences between distant and nearby supernovae of the same nominal type. More distant supernovae are seen in younger galaxies, because of the light travel time, and these younger galaxies tend to have more massive rapidly evolving stars with lower heavy element abundances. How do we know the properties of the supernovae are not also different? We recommend Leibundgut's (2001, Sec. 4) discussion of the astrophysical hazards. Astronomers have checks for this and other issues of interpretation of the observations used in the cosmological tests. But it takes nothing away from this careful and elegant work to note that the checks seldom can be convincing, because the astronomy is complicated and what can be observed is sparse. What is more, we don't know ahead of time that the physics that is well tested on scales ranging from the laboratory to the Solar System survives the enormous extrapolation to cosmology.
Our first point is that the situation is by no means hopeless, because we now have significant cross-checks from the consistency of results based on independent applications of the astronomy and of the physics of the cosmological model. If the physics or astronomy were faulty we would not expect consistency from independent lines of evidence -- apart from the occasional accident, and the occasional tendency to stop the analysis when it approachs the "right answer". We have to demand abundant evidence of consistency, and that is starting to appear.
The case for detection of
 or dark energy
commences with
the Friedmann-Lemaître cosmological model. In this
model the expansion history of the universe is determined by a
set of dimensionless parameters whose sum is normalized to unity,
or dark energy
commences with
the Friedmann-Lemaître cosmological model. In this
model the expansion history of the universe is determined by a
set of dimensionless parameters whose sum is normalized to unity,
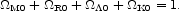 |
(1) |
The first,
 M0, is a
measure of the present mean mass density in nonrelativistic matter,
mainly baryons and nonbaryonic dark matter. The second,
M0, is a
measure of the present mean mass density in nonrelativistic matter,
mainly baryons and nonbaryonic dark matter. The second,
 R0 ~ 1
× 10-4,
is a measure of the present mass in the relativistic 3 K thermal
cosmic microwave background radiation that almost homogeneously
fills space, and the accompanying low mass
neutrinos. The third is a measure of
R0 ~ 1
× 10-4,
is a measure of the present mass in the relativistic 3 K thermal
cosmic microwave background radiation that almost homogeneously
fills space, and the accompanying low mass
neutrinos. The third is a measure of
 or the
present value of the dark energy equivalent. The fourth,
or the
present value of the dark energy equivalent. The fourth,
 K0, is an
effect of the curvature of space. We review some
details of these parameters in the next section, and of their
measurements in Sec. IV.
K0, is an
effect of the curvature of space. We review some
details of these parameters in the next section, and of their
measurements in Sec. IV.
The most direct evidence for detection of dark energy comes from
observations of supernovae of a type whose intrinsic
luminosities are close to uniform (after subtle astronomical
corrections, a few details of which are discussed in
Sec. IV.B.4). The observed
brightness as a function of the wavelength shift of the radiation
probes the geometry of spacetime, in what has come to be
called the redshift-magnitude relation.
2 The measurements agree
with the relativistic cosmological model with
 K0 = 0,
meaning no space curvature, and
K0 = 0,
meaning no space curvature, and

 0 ~
0.7, meaning nonzero
0 ~
0.7, meaning nonzero
 . A model with
. A model with

 0 =
0 is two or three standard
deviations off the best fit, depending on the data set and
analysis technique. This is an important indication, but 2 to 3
0 =
0 is two or three standard
deviations off the best fit, depending on the data set and
analysis technique. This is an important indication, but 2 to 3
 is not convincing, even
when we can be sure the
systematic errors are under reasonable control. And we have
to consider that there may be a significant systematic error
from differences between distant, high redshift, and nearby,
low redshift, supernovae.
is not convincing, even
when we can be sure the
systematic errors are under reasonable control. And we have
to consider that there may be a significant systematic error
from differences between distant, high redshift, and nearby,
low redshift, supernovae.
There is a check, based on the CDM model
3
for structure formation. The fit of the model to the observations
reviewed in Sec. IV.B yields two key
constraints. First, the
angular power spectrum of fluctuations in the temperature of the
3 K thermal cosmic microwave background radiation across the sky
indicates
 K0 is
small. Second, the power spectrum of the
spatial distribution of the galaxies requires
K0 is
small. Second, the power spectrum of the
spatial distribution of the galaxies requires
 M0 ~ 0.25.
Similar estimates of
M0 ~ 0.25.
Similar estimates of
 M0 follow
from independent lines of observational evidence. The rate of
gravitational lensing prefers a somewhat larger value (if
M0 follow
from independent lines of observational evidence. The rate of
gravitational lensing prefers a somewhat larger value (if
 K0 is
small), and some dynamical analyses of systems of galaxies prefer lower
K0 is
small), and some dynamical analyses of systems of galaxies prefer lower
 M0. But the
differences could all be in the measurement uncertainties. Since
M0. But the
differences could all be in the measurement uncertainties. Since
 R0 in
Eq. (1) is small, the conclusion is
R0 in
Eq. (1) is small, the conclusion is

 0 is
large, in excellent agreement with what the supernovae say.
0 is
large, in excellent agreement with what the supernovae say.
Caution is in order, however, because this check depends on the CDM model for structure formation. We can't see the dark matter, so we naturally assign it the simplest properties we can get away with. Maybe it is significant that the model has observational problems with galaxy formation, as discussed in Sec. IV.A.2, or maybe these problems are only apparent, from the complications of the astronomy. We are going to have to determine which it is before we can have a lot of confidence in the role of the CDM model in the cosmological tests. We will get a strong hint from the precision measurements in progress of the angular distribution of the 3 K thermal cosmic microwave background radiation. 4 If the results match in all detail the prediction of the relativistic model for cosmology and the CDM model for structure formation, with parameter choices that agree with the constraints from all the other cosmological tests, it will be strong evidence that we are approaching a good approximation to reality, and the completion of the great program of cosmological tests that commenced in the 1930s. But all that is to come.
We emphasize that the advances in the empirical basis for
cosmology already are very real and substantial.
How firm is the conclusion depends on the issue, of course. Every
competent cosmologist we know accepts as established beyond
reasonable doubt that the universe is expanding and cooling in a
near homogeneous and isotropic way from a hotter denser state:
how else could space, which is transparent now, have been filled
with radiation that has relaxed to a thermal spectrum? The debate
is about when the expansion commenced or became a meaningful
concept. Some whose opinions and research we respect
question the extrapolation of the gravitational inverse square
law, in its use in estimates of masses in galaxies and systems of
galaxies, and of
 M0. We
agree that this law is one of the hypotheses to be tested. Our
conclusion from the cosmological tests in
Sec. IV is that the law
passes significant though not yet complete tests, and that we
already have a strong scientific case, resting on the abundance of
cross-checks, that the matter density parameter
M0. We
agree that this law is one of the hypotheses to be tested. Our
conclusion from the cosmological tests in
Sec. IV is that the law
passes significant though not yet complete tests, and that we
already have a strong scientific case, resting on the abundance of
cross-checks, that the matter density parameter
 M0 is about
one quarter. The case for detection of
M0 is about
one quarter. The case for detection of

 0 is
significant too, but not yet as compelling.
0 is
significant too, but not yet as compelling.
For the most part the results of the cosmological tests agree wonderfully well with accepted theory. But the observational challenges to the tests are substantial: we are drawing profound conclusions from very limited information. We have to be liberal in considering ideas about what the universe is like, conservative in accepting ideas into the established canon.
2 The apparent magnitude is m = - 2.5 log10f plus a constant, where f is the detected energy flux density in a chosen wavelength band. The standard measure of the wavelength shift, due to the expansion of the universe, is the redshift z defined in Eq. (7) below. Back.
3 The model is named after the nonbaryonic cold dark matter (CDM) that is assumed to dominate the masses of galaxies in the present universe. There are more assumptions in the CDM model, of course; they are discussed in Secs. III.D and IV.A.2. Back.
4 At the time of writing the MAP satellite is taking data; the project is described in http://map.gsfc.nasa.gov/. Back.