A. The theories

1. General relativity

Some early discussions of the cosmological tests, as in Robertson (1955) and Bondi (1961), make the point that observationally important elements of a spatially homogeneous cosmology follow by symmetry, independent of general relativity. This means some empirical successes of the cosmology are not tests of relativity. The point was important in the 1950s, because the Steady State theory was a viable alternative to the Friedmann-Lemaître cosmology, and because the experimental tests of relativity were quite limited.

The tests of general relativity are much better now, but cosmology still is a considerable extrapolation. The length scales characteristic of the precision tests of general relativity in the Solar System and binary pulsar are 10¹³ cm. An important scale for cosmology is the Hubble length, H₀^-1 ~ 5000 Mpc ~ 10²⁸ cm, fifteen orders of magnitude larger. An extrapolation of fifteen orders of magnitude in energy from that achieved at the largest accelerators, ~ 10¹² eV, brings us to the very different world of the Planck energy. Why is the community not concerned about an extrapolation of similar size in the opposite direction? One reason is that the known open issues of physics have to do with small length scales; there is no credible reason to think general relativity may fail on large scales. This is comforting, to be sure, but, as indicated in footnote 7, not the same as a demonstration that we really know the physics of cosmology. Another reason is that if the physics of cosmology were very different from general relativity it surely would have already been manifest in serious problems with the cosmological tests. This also is encouraging, but we have to consider details, as follows.

One sobering detail is that in the standard cosmology the two dominant contributions to the stress-energy tensor -- dark energy and dark matter -- are hypothetical, introduced to make the theories fit the observations (Eq. [2]). This need not mean there is anything wrong with general relativity -- we have no reason to expect Nature to have made all matter readily observable other than by its gravity -- but it is a cautionary example of the challenges. Milgrom's (1983) modified Newtonian dynamics (MOND) replaces the dark matter hypothesis with a hypothetical modification of the gravitational force law. MOND gives remarkably successful fits to observed motions within galaxies, without dark matter (de Blok et al., 2001). So why should we believe there really is cosmologically significant mass in nonbaryonic dark matter? Unless we are lucky enough to get a laboratory detection, the demonstration must be through the tests of the relativistic cosmology (and any other viable cosmological models that may come along, perhaps including an extension of MOND). This indirect chain of evidence for dark matter is becoming tight. A new example -- the prospect for a test of the inverse square law for gravity on the length scales of cosmology -- is striking enough for special mention here. ⁵⁹

Consider the equation of motion ⁶⁰ of a freely moving test particle with nonrelativistic peculiar velocity in a universe with expansion factor a(t),

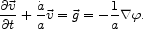(51)

The particle always is moving toward receding observers, which produces the second term in the left-most expression. The peculiar gravitational acceleration 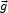relative to the homogeneous background model is computed from the Poisson equation for the gravitational potential ,

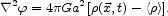(52)

The mean mass density <> is subtracted because 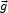is computed relative to the homogeneous model. The equation of mass conservation expressed in terms of the density contrast = / <> - 1 of the mass distribution modeled as a continuous pressureless fluid is

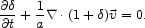(53)

In linear perturbation theory in and these equations give

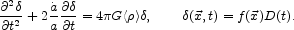(54)

Here D(t) is the growing solution to the first equation. ⁶¹ The velocity field belonging to the solution D(t) is the inhomogeneous solution to Eq. (53) in linear perturbation theory,

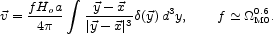(55)

The factor f = d log D / d log a depends on the cosmological model; the second equation is a good approximation if = 0 or space curvature vanishes. ⁶² One sees from Eq. (55) that the peculiar velocity is proportional to the gravitational acceleration, as one would expect in linear theory.

The key point of Eq. (54) for the present purpose is that the evolution of the density contrast at a given position is not affected by the value of anywhere else. This is a consequence of the inverse square law. The mass fluctuation in a chosen volume element produces a peculiar gravitational acceleration 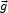that produces a peculiar velocity field 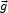that has zero divergence and so the mass inside the volume element does not effect the exterior.

For a "toy" model of the effect of a failure of the inverse square law, suppose we adjust the expression for the peculiar gravitational acceleration produced by a given mass distribution to

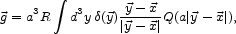(56)

where R is some function of world time only. In standard gravity physics Q(w) = w^-2. We have no basis in fundamental physics for any other function of w. Although Milgrom's (1983) MOND provides a motivation, Eq. (56) is not meant to be an extension of MOND to large-scale flows. It is an ad hoc model that illustrates an important property of the inverse square law.

We noted that in linear theory 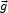. Thus we find that the divergence of Eq. (56), with the mass conservation equation (53) in linear perturbation theory, gives

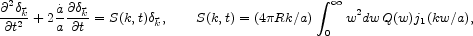(57)

where 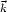(t) is the Fourier transform of the mass density contrast (, t) and j₁ is a spherical Bessel function. The inverse square law, Q = w^-2, makes the factor S independent of the wavenumber k. This means all Fourier amplitudes grow by the same factor in linear perturbation theory (when the growing mode dominates), so the functional form of (, t) is preserved and the amplitude grows, as Eq. (54) says. When Q is some other function, the phases of the 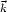are preserved but the functional form of the power spectrum |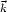|² evolves. For example, if Q w^n-2 with -2 < n < 1 (so the integral in Eq. [57] does not diverge) Eq. (57) is

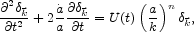(58)

where U is some function of world time.

If n > 0 density fluctuations grow faster on larger scales. If Q(w) follows Newtonian gravity on the scale of galaxies and bends to n > 0 on larger scales it reduces the mean mass density needed to account for the measured large-scale galaxy flows, and maybe reduces the need for dark matter. But there are testable consequences: the apparent value of _M0 would vary with the length scale of the measurement, and the form of the power spectrum of the present mass distribution would not agree with the form at redshift z ~ 1000 when it produced the observed angular power spectrum of the 3 K cosmic microwave background. Thus we are very interested in the evidence of consistency of these tests (as discussed in Sec. IV.B.13).

2. The cold dark matter model for structure formation

Important cosmological tests assume the CDM model for structure formation (Sec. III.C), so we must consider tests of the model. The model has proved to be a useful basis for analyses of the physics of formation of galaxies and clusters of galaxies (e.g., Kay et al., 2002; Colberg et al., 2000; and references therein). There are issues to consider, however; Sellwood and Kosowsky (2001) give a useful survey of the situation. We remark on recent developments and what seem to us to be critical issues.

Numerical simulations of the dark mass distribution in the CDM model predict that massive halos have many low mass satellites, perhaps significantly more than the number observed around the Milky Way galaxy (Klypin et al., 1999; Moore et al., 1999a). The issue is of great interest but not yet a critical test, because it is difficult to predict the nature of star formation in a low mass dark halo: what does a dark halo look like when star formation or the neutral gas content makes it visible? For recent discussions see Tully et al. (2002) and Stoehr et al. (2002).

The nature of the dark mass distribution within galaxies is a critical issue, because we know where to look for a distinctive CDM feature: a cusp-like central mass distribution, the density varying with radius r as r^- with 1. The power law is not unexpected, because there is nothing in the CDM model to fix an astronomically interesting value for a core radius. ⁶³ A measure of the mass distribution in disk galaxies is the rotation curve: the circular velocity as a function of radius for matter supported by rotation. In some low surface brightness galaxies the observed rotation curves are close to solid body, v_c r, near the center, consistent with a near homogeneous core, and inconsistent with the cusp-like CDM mass distribution. ⁶⁴

The circular velocity produced by the mass distribution r^-1 is not very different from solid body, or from the observations, and the difference might be erased by gravitational rearrangement of the dark mass by the fluctuations in the distribution of baryonic mass driven by star formation, winds, or supernovae. This is too complicated to assess by current numerical simulations. But we do have a phenomenological hint: central solid body rotation is most clearly seen in the disk-like galaxies with the lowest surface brightnesses, the objects in which the baryon mass seems least likely to have had a significant gravitational effect on the dark mass. This challenge to the CDM model is pressing.

The challenge may be resolved in a warm dark matter model, where the particles are assigned a primeval velocity dispersion that suppresses the initial power spectrum of density fluctuations on small scales (Moore et al., 1999b; Sommer-Larsen and Dolgov, 2001; Bode, Ostriker, and Turok, 2001). But it seems to be difficult to reconcile the wanted suppression of small-scale power with the observation of small-scale clustering in the Lyman- forest -- the neutral hydrogen observed at z ~ 3 in the Lyman- resonance absorption lines in quasar spectra (Narayanan et al., 2000; Knebe et al., 2002). Spergel and Steinhardt (2000) point out that the scattering cross section of self-interacting cold dark matter particles can be adjusted to suppress the cusp-like core. ⁶⁵ Davé et al. (2001) demonstrate the effect in numerical simulations. But Miralda-Escudé (2002) points out that the collisions would tend to make the velocity distribution isotropic, contrary to the evidence for ellipsoidal distributions of dark matter in clusters of galaxies. For recent surveys of the very active debate on these issues see Primack (2002) and Tasitsiomi (2002); for references to still other possible fixes see Davé et al. (2001).

Another critical issue traces back to the biasing picture discussed in Sec. III.D. If _M0 is well below unity there need not be significant mass in the voids defined by the large galaxies. But the biasing process still operates, and might be expected to cause dwarf or irregular galaxies to trespass into the voids outlined by the large regular galaxies. This seems to happen in CDM model simulations to a greater extent than is observed. Mathis and White (2002) discuss voids in CDM simulations, but do not address the trespassing issue. The reader is invited to compare the relative distributions of big and little galaxies in the simulation in Fig. 1 of Mathis and White (2002) with the examples of observed distributions in Figs. 1 and 2 in Peebles (1989b) and in Figs. 1 to 3 in Peebles (2001).

The community thought is that the trespassing issue need not be a problem for the CDM model: the low mass density in voids disfavors formation of galaxies from the debris left in these regions. But we have not seen an explanation of why local upward mass fluctuations, of the kind that produce normal galaxies in populated regions, and appear also in the predicted debris in CDM voids, fail to produce dwarf or irregular void galaxies. An easy explanation is that the voids contain no matter, having been gravitationally emptied by the growth of primeval non-Gaussian mass density fluctuations. The evidence in tests (10) and (11) in Sec. IV.B is that the initial conditions are close to Gaussian. But non-Gaussian initial conditions that reproduce the character of the galaxy distribution, including suppression of the trespassing effect, would satisfy test (10) by construction.

We mention finally the related issues of when the large elliptical galaxies formed and when they acquired the central compact massive objects that are thought to be remnant quasar engines (Lynden-Bell, 1969).

In the CDM model large elliptical galaxies form in substantial numbers at redshift z < 1. Many astronomers do not see this as a problem, because ellipticals do tend to contain relatively young star populations, and some elliptical galaxies have grown by recent mergers, as predicted in the CDM model. ⁶⁶ But prominent merger events are rare, and the young stars seen in ellipticals generally seem to be a "frosting" (Trager et al., 2000) of recent star formation on a dominant old star population. The straightforward reading of the evidence assembled in Peebles (2002) is that most of the large ellipticals are present as assembled galaxies of stars at z = 2. ⁶⁷ The CDM model prediction is uncertain because it depends on the complex processes of star formation that are so difficult to model. The reading of the situation by Thomas and Kauffmann (1999) is that the predicted abundance of giant ellipticals at z = 2 is less than about one third of what it is now. Deciding whether the gap between theory and observation can be closed is not yet straightforward.

A related issue is the significance of the observations of quasars at redshift z ~ 6. By conventional estimates ⁶⁸ these quasars are powered by black holes with masses at the upper end of the range of masses of the central compact objects -- let us call them black hole quasar remanants -- in the largest present-day elliptical galaxies. Here are some options to consider. First, the high redshift quasars may be in the few large galaxies that have already formed at z ~ 6. Wyithe and Loeb (2002), following Efstathiou and Rees (1988), show that this fits the CDM model if the quasars at z ~ 6 have black hole mass ~ 10⁹ M in dark halos with mass ~ 10¹² M. In the CDM picture these early galaxies would be considerably denser than normal galaxies; to be checked is whether they would be rare enough to be observationally acceptable. Second, the quasars at z ~ 6 may be in more modest star clusters that later grew by merging into giant ellipticals. To be established is whether this growth would preserve the remarkably tight correlation between the central black hole mass and the velocity dispersion of the stars ⁶⁹, and whether growth by merging would produce an acceptable upper bound on black hole masses at the present epoch. Third, large ellipticals might have grown by accretion around pre-existing black holes, without a lot of merging. This is explored by Danese et al. (2002).

There does not seem to be a coherent pattern to the present list of challenges to the CDM model. The rotation curves of low surface brightness galaxies suggest we want to suppress the primeval density fluctuations on small scales, but the observations of what seem to be mature elliptical galaxies at high redshifts suggest we want to increase small-scale fluctuations, or maybe postulate non-Gaussian fluctuations that grow into the central engines for quasars at z ~ 6. We do not want these central engines to appear in low surface brightness galaxies, of course.

It would not be at all surprising if the confusion of challenges proved to be at least in part due to the difficulty of comparing necessarily schematic analytic and numerical model analyses to the limited and indirect empirical constraints. But it is also easy to imagine that the CDM model has to be refined because the physics of the dark sector of matter and energy is more complicated than CDM, and maybe even more complicated than any of the alternatives now under discussion. Perhaps some of the structure formation ideas people were considering a decade ago, which invoke good physics, also will prove to be significant factors in relieving the problems with structure formation. And the important point for our purpose is that we do not know how the relief might affect the cosmological tests.

⁵⁹ Binétruy and Silk (2001) and Uzan and Bernardeau (2001) pioneered this probe of the inverse square law. Related probes, based on the relativistic dynamics of gravitational lensing and the anisotropy of the 3 K thermal background, are discussed by these authors and White and Kochanek (2001). Back.

⁶⁰ These relations are discussed in many books on cosmology, including Peebles (1980a). Back.

⁶¹ The general solution is a sum of the growing and decaying solutions, but because the universe has expanded by a large factor since nongravitational forces were last important on large scales we can ignore the decaying part. Back.

⁶² This is illustrated in Fig. 13.14 in Peebles (1993). An analytic expression for spherical symmetry is derived by Lightman and Schechter (1990). Back.

⁶³ Pioneering work on the theory of the central mass distribution in a dark mass halo is in Dubinski and Carlberg (1991). Moore (1994) and Flores and Primack (1994) are among the first to point out the apparent disagreement between theory and observation. Back.

⁶⁴ The situation is reviewed by de Blok et al. (2001), and de Blok and Bosma (2002). The galaxy NGC 3109 is a helpful example because it is particularly close -- just outside the Local Group -- and so particularly well resolved. An optical image is in plate 39 in the Hubble Atlas of Galaxies (Sandage, 1961b). The radial velocity measurements across the face of the galaxy, in Figs. 1 and 2 in Blais-Ouellette, Amram, and Carignan (2001), are consistent with circular motion with v_c r at r 2 kpc. Back.

⁶⁵ In a power law halo with r^-, the velocity dispersion varies with radius as <v²> ~ GM( < r) / r r^2-. The particle scattering cross section must be adjusted to erase the effective temperature gradient, thus lowering the mass density at small radii, without promoting unacceptable core collapse. Back.

⁶⁶ The classic merger example is also the nearest large elliptical galaxy, Centaurus A (NGC 5128). The elliptical image is crossed by a band of gas and dust that likely is the result of a merger with one of the spiral galaxies in the group around this elliptical. For a thorough review of what is known about this galaxy see Israel (1998). Back.

⁶⁷ Papovich, Dickinson, and Ferguson (2002) find evidence that the comoving number density of all galaxies with star mass greater than 1 × 10¹⁰ M, where M is the mass of the Sun, is significantly less at redshift z > 1 than now. This is at least roughly in line with the distribution of star ages in the Milky Way spiral galaxy: the bulge stars are old, while the stars in the thin disk have a broad range of ages. Thus if this galaxy evolved from z = 2 without significant growth by mergers its star mass at z = 2 would be significantly less than the present value, which is about 5 × 10¹⁰ M. Cimatti et al. (2002) show that the redshift distribution of faint galaxies selected at wavelenght ~ 2 µm is not inconsistent with the picture that galaxy evolution at z < 2 is dominated by ongoing star formation rather than merging. Back.

⁶⁸ The quasars discovered in the Sloan Digital Sky Survey are discussed by Fan et al. (2001). If the quasar radiation is not strongly beamed toward us, its luminosity translates to an Eddington mass (the mass at which the gravitational pull on unshielded plasma balances the radiation pressure) M_bh ~ 10^9.3 M. In a present-day elliptical galaxy with this mass in the central compact object the line of sight velocity dispersion is 350 km s^-1. This is close to the highest velocity dispersion observed in low redshift elliptical galaxies. For example, in the Faber et al. (1989) catalog of 500 ellipticals, 15 have 300 < < 400 km s^-1, and none has a larger . From the present-day relation between and luminosity, an elliptical galaxy with = 350 km s^-1 has mass ~ 10^12.3 M in stars. The dark matter associated with this many baryons is M_DM ~ 10¹³ M. This is a large mass to assemble at z ~ 6, but it helps that such objects are rare. The present number density of giant elliptical galaxies with > 300 km s^-1 is about 10^-5 Mpc^-3, four orders of magnitude more than the comoving number density of quasars detected at z ~ 6. Back.

⁶⁹ Ferrarese and Merritt (2000) and Gebhardt et al. (2000) show that the black hole mass correlates with the velocity dispersion of the stars in an elliptical galaxy and the velocity dispersion of the bulge stars in a spiral galaxy. This is not a direct gravitational effect: the black hole mass is less than 1% of the star mass in the bulge or the elliptical galaxy. Back.