B. The tests

The literature on the cosmological tests is enormous compared to what it was just a decade ago, and growing. Our references to this literature are much sparser than in Sec. III, on the principle that no matter how complete the list it will be out of date by the time this review is published. For the same reason, we do not attempt to present the best values of the cosmological parameters based on their joint fit to the full suite of present measurements. The situation will continue to evolve as the measurements improve, and the state of the art is best followed on astro-ph. We do take it to be our assignment to consider what the tests are testing, and to assess the directions the results seem to be leading us. The latter causes us to return many times to two results that seem secure because they are so well checked by independent lines of evidence, as follows.

First, at the present state of the tests, optically selected galaxies are useful mass tracers. By that we mean the assumption that visible galaxies trace mass does not seriously degrade the accuracy of analyses of the observations. This will change as the measurements improve, of course, but the case is good enough now that we suspect the evidence will continue to be that optically selected galaxies are good indicators of where most of the mass is at the present epoch. Second, the mass density in matter is significantly less than the critical Einstein-de Sitter value. The case is compelling because it is supported by so many different lines of evidence (as summarized in Sec. IV.C). Each could be compromised by systematic error, to be sure, but it seems quite unlikely the evidence could be so consistent yet misleading. A judgement of the range of likely values of the mass density is more difficult. Our estimate, based on the measurements we most trust, is

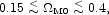(59)

and we would put the central value at _M0 0.25. The spread is meant in the sense of two standard deviations: we would be surprised to find _M0 is outside this range.

Several other policy decisions should be noted. The first is that we do not comment on tests that have been considered but not yet applied in a substantial campaign of measurements. A widely discussed example is the Alcock and Paczynski (1979) comparison of the apparent depth and width of a system from its angular size and depth in redshift.

In analyses of the tests of models for evolving dark energy density, simplicity recommends the XCDM parametrization with a single constant parameter w_X, as is demonstrated by the large number of recent papers on this approach. But the more complete physics recommends the scalar field model with an inverse power-law potential. This includes the response of the spatial distribution of the dark energy to the peculiar gravitational field. Thus our comments on variable dark energy density are more heavily weighted to the scalar field model than is the case in the recent literature.

The gravitational deflection of light appears not only as a tool in cosmological tests, as gravitational lensing, but also as a source of systematic error. The gravitational deflections caused by mass concentrations magnify the image of a galaxy along a line of sight where the mass density is larger than the average, and reduce the solid angle of the image when the mass density along the line of sight is low. The observed energy flux density is proportional to the solid angle (because the surface brightness, erg cm^-2 s^-1 ster^-1 Hz^-1, is conserved at fixed redshift). Selection can be biased either way, by the magnification effect or by obscuration by the dust that tends to accompany mass. ⁷⁰ When the tests are more precise we will have to correct them for these biases, through models for the mass distribution (as in Premadi et al., 2001), and the measurements of the associated gravitational shear of the shapes of the galaxy images. But the biases seem to be small and will not be discussed here.

And finally, as the cosmological tests improve a satisfactory application will require a joint fit of all of the parameters to all of the relevant measurements and constraints. Until recently it made sense to impose prior conditions, most famously the hope that if the universe is not well described by the Einstein-de Sitter model then surely it is the case either that is negligibly small or else that space curvature may be neglected. We suspect the majority in the community still expect this is true, on the basis of the coincidences argument in Sec. II.B.2, but it will be important to see what comes out of joint fits of both _M0 and ₀, as well as all the other parameters, as is becoming the current practice. Our test-by-test discussion is useful for sorting out the physics and astronomy, we believe; it is not the prototype for the coming generations of precision application of the tests.

Our remarks are ordered by our estimates of the model dependence.

1. The thermal cosmic microwave background radiation

We are in a sea of radiation with spectrum very close to Planck at T = 2.73 K, and isotropic to one part in 10⁵ (after correction for a dipole term that usually is interpreted as the result of our motion relative to the rest frame defined by the radiation). ⁷¹ The thermal spectrum indicates thermal relaxation, for which the optical depth has to be large on the scale of the Hubble length H₀^-1. We know space now is close to transparent at the wavelengths of this radiation, because radio galaxies are observed at high redshift. Thus the universe has to have expanded from a state quite different from now, when it was hotter, denser, and optically thick. This is strong evidence our universe is evolving.

This interpretation depends on, and checks, conventional local physics with a single metric description of spacetime. Under these assumptions the expansion of the universe preserves the thermal spectrum and cools the temperature as ⁷²

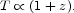(60)

Bahcall and Wolf (1968) point out that one can test this temperature-redshift relation by measurements of the excitation temperatures of fine-structure absorption line systems in gas clouds along quasar lines of sight. The corrections for excitations by collisions and the local radiation field are subtle, however, and perhaps not yet fully sorted out (as discussed by Molaro et al., 2002, and references therein).

The 3 K thermal cosmic background radiation is a centerpiece of modern cosmology, but its existence does not test general relativity.

2. Light element abundances

The best evidence that the expansion and cooling of the universe traces back to high redshift is the success of the standard model for the origin of deuterium and isotopes of helium and lithium, by reactions among radiation, leptons, and atomic nuclei as the universe expands and cools through temperature T ~ 1 MeV at redshift z ~ 10¹⁰. The free parameter in the standard model is the present baryon number density. The model assumes the baryons are uniformly distributed at high redshift, so this parameter with the known present radiation temperature fixes the baryon number density as a function of temperature and the temperature as a function of time. The latter follows from the expansion rate Eq. (11), which at the epoch of light element formation may be written as

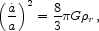(61)

where the mass density _r counts radiation, which is now at T = 2.73 K, the associated neutrinos, and e^± pairs. The curvature and terms are unimportant, unless the dark energy mass density varies quite rapidly.

Independent analyses of the fit to the measured element abundances, corrected for synthesis and destruction in stars, by Burles, Nollett, and Turner (2001), and Cyburt, Fields, and Olive (2001), indicate

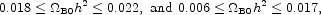(62)

both at 95% confidence limits. Other analyses by Coc et al. (2002) and Thuan and Izotov (2002) result in ranges that lie between the two of Eq. (62). The difference in values may be a useful indication of remaining uncertainties; it is mostly a consequence of the choice of isotopes used to constrain _B0 h². Burles et al. (2001) use the deuterium abundance, Cyburt et al. (2001) favor the helium and lithium measurements, and the other two groups use other combinations of abundances. Equation. (62) is consistent with the summary range, 0.0095 _B0 h² 0.023 at 95% confidence, of Fields and Sarkar (2002).

The baryons observed at low redshift, in stars and gas, amount to (Fukugita, Hogan, and Peebles, 1998)

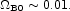(63)

It is plausible that the difference between Eqs. (62) and (63) is in cool plasma, with temperature T ~ 100 eV, in groups of galaxies. It is difficult to observationally constrain the idea that there is a good deal more cool plasma in the large voids between the concentrations of galaxies. A more indirect but eventually more precise constraint on _B0, from the anisotropy of the 3 K thermal cosmic microwave background radiation, is discussed in test (11).

It is easy to imagine complications, such as inhomogeneous entropy per baryon, or in the physics of neutrinos; examples may be traced back through Abazajian, Fuller, and Patel (2001) and Giovannini, Keihänen, and Kurki-Suonio (2002). It seems difficult to imagine that a more complicated theory would reproduce the successful predictions of the simple model, but Nature fools us on occasion. Thus before concluding that the theory of the pre-stellar light element abundances is known, apart from the addition of decimal places to the cross sections, it is best to wait and see what advances in the physics of baryogenesis and of neutrinos teach us.

How is general relativity probed? The only part of the computation that depends specifically on this theory is the pressure term in the active gravitational mass density, in the expansion rate equation (8). If we did not have general relativity, a simple Newtonian picture might have led us to write down / a = - 4 G _r / 3 instead of Eq. (8). With _r ~ 1 / a⁴, as appropriate since most of the mass is fully relativistic at the redshifts of light element production, this would predict the expansion time a / is 2^1/2 times the standard expression (that from Eq. [61]). The larger expansion time would hold the neutron to proton number density ratio close to that at thermal equilibrium, n/p = e^-Q/kT, where Q is the difference between the neutron and proton masses, to lower temperature. It would also allow more time for free decay of the neutrons after thermal equilibrium is broken. Both effects decrease the final ⁴He abundance. The factor 2^1/2 increase in expansion time would reduce the helium abundance by mass to Y ~ 0.20. This is significantly less than what is observed in objects with the lowest heavy element abundances, and so seems to be ruled out (Steigman, 2002). ⁷³ That is, we have positive evidence for the relativistic expression for the active gravitational mass density at redshift z ~ 10¹⁰, a striking result.

3. Expansion times

The predicted time of expansion from the very early universe to redshift z is

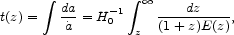(64)

where E(z) is defined in Eq. (11). If = 0 the present age is t₀ < H₀^-1. In the Einstein-de Sitter model the present age is t₀ = 2 / (3H₀). If the dark energy density is significant and evolving, we may write = ₀ f (z), where the function of redshift is normalized to f (0) = 1. Then E(z) generalizes to

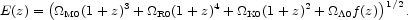(65)

In the XCDM parametrization with constant w_X (Eq. [45]), f (z) = (1 + z)^3(1+w_X). Olson and Jordan (1987) present the earliest discussion we have found of H₀ t₀ in this picture (before it got the name). In scalar field models, f (z) generally must be evaluated numerically; examples are in Peebles and Ratra (1988).

The relativistic correction to the active gravitational mass density (Eq. [8]) is not important at the redshifts at which galaxies can be observed and the ages of their star populations estimated. At moderately high redshift, where the nonrelativistic matter term dominates, Eq. (64) is approximately

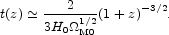(66)

That is, the ages of star populations at high redshift are an interesting probe of _M0 but they are not very sensitive to space curvature or to a near constant dark energy density. ⁷⁴

Recent analyses of the ages of old stars ⁷⁵ indicate the expansion time is in the range

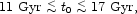(67)

at 95% confidence, with central value t₀ 13 Gyr. Following Krauss and Chaboyer (2001) these numbers add 0.8 Gyr to the star ages, under the assumption star formation commenced no earlier than z = 6 (Eq. [66]). A naive addition in quadrature to the uncertainty in H₀ (Eq. [6]) indicates the dimensionless age parameter is in the range

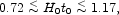(68)

at 95% confidence, with central value H₀ t₀ 0.89. The uncertainty here is dominated by that in t₀. In the spatially-flat CDM model (_K0 = 0), Eq. (68) translates to 0.15 _M0 0.8, with central value _M0 0.4. In the open model with ₀ = 0, the constraint is _M0 0.6 with the central value _M0 0.1. In the inverse power-law scalar field dark energy case (Sec. II.C) with power-law index = 4, the constraint is 0.05 _M0 0.8.

We should pause to admire the unification of the theory and measurements of stellar evolution in our galaxy, which yield the estimate of t₀, and the measurements of the extragalactic distance scale, which yield H₀, in the product in Eq. (68) that agrees with the relativistic cosmology with dimensionless parameters in the range now under discussion. As we indicated in Sec. III, there is a long history of discussion of the expansion time as a constraint on cosmological models. The measurements now are tantalizingly close to a check of consistency with the values of _M0 and ₀ indicated by other cosmological tests.

4. The redshift-angular size and redshift-magnitude relations

An object at redshift z with physical length l perpendicular to the line of sight subtends angle such that

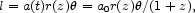(69)

where a₀ = a(t₀). The angular size distance r(z) is the coordinate position of the object in the first line element in Eq. (15), with the observer placed at the origin. The condition that light moves from source to observer on a radial null geodesic is

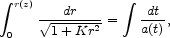(70)

which gives

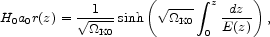(71)

where E(z) is defined in Eqs. (11) and (65).

In the Einstein-de Sitter model, the angular-size-redshift relation is

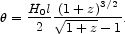(72)

At z << 1, = H₀ l / z, consistent with the Hubble redshift-distance relation. At z >> 1 the image is magnified, ⁷⁶ 1 + z.

The relation between the luminosity of a galaxy and the energy flux density received by an observer follows from Liouville's theorem: the observed energy flux i₀ per unit time, area, solid angle, and frequency satisfies

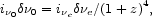(73)

with i_e the emitted energy flux (surface brightness) at the source and _e = ₀(1 + z) the bandwidth at the source at redshift z. The redshift factor (1 + z)⁴ appears for the same reason as in the 3 K cosmic microwave background radiation energy density. With Eq. (69) to fix the solid angle, Eq. (73) says the observed energy flux per unit area, time, and frequency from a galaxy at redshift z that has luminosity L_e per frequency interval measured at the source is

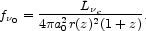(74)

In conventional local physics with a single metric theory the redshift-angular size (Eq. [69]) and redshift-magnitude (Eq. [7]) relations are physically equivalent. ⁷⁷

The best present measurement of the redshift-magnitude relation uses supernovae of Type Ia. ⁷⁸ The results are inconsistent with the Einstein-de Sitter model, at enough standard deviations to make it clear that unless there is something quite substantially and unexpectedly wrong with the measurements the Einstein-de Sitter model is ruled out. The data require > 0 at two to three standard deviations, depending on the choice of data and method of analysis (Leibundgut, 2001; Gott et al., 2001). The spatially-flat case with _M0 in the range of Eq. (59) is a good fit for constant . The current data do not provide interesting constraints on the models for evolving dark energy density. ⁷⁹ Perlmutter et al. (http://snap.lbl.gov/) show that a tighter constraint, from supernovae observations to redshift z ~ 2, by the proposed SNAP satellite, is feasible and capable of giving a significant detection of and maybe its evolution. ⁸⁰

5. Galaxy counts

Counts of galaxies -- or of other objects whose number density as a function of redshift may be modeled -- probe the volume element (dV / dz)dz defined by a solid angle in the sky and a redshift interval dz. The volume is fixed by the angular size distance (Eq. [69]), which determines the area subtended by the solid angle, in combination with the redshift-time relation (Eq. [64]), which fixes the radial distance belonging to the redshift interval.

Sandage (1961a) and Brown and Tinsley (1974) showed that with the technology then available galaxy counts are not a very sensitive probe of the cosmological parameters. Loh and Spillar (1986) opened the modern exploration of the galaxy count-redshift relation at redshifts near unity, where the predicted counts are quite different in models with and without a cosmological constant (as illustrated in Figure 13.8 in Peebles, 1993).

The interpretation of galaxy counts requires an understanding of the evolution of galaxy luminosities and the gain and loss of galaxies by merging. Here is an example of the former in a spatially-flat cosmological model with _M0 = 0.25. The expansion time from high redshift is t₃ = 2.4 Gyr at redshift z = 3 and t₀ = 15 Gyr now. Consider a galaxy observed at z = 3. Suppose the bulk of the stars in this galaxy formed at time t_f, and the population then aged and faded without significant later star formation. Then if t_f << t₃ the ratio of the observed luminosity at z = 3 to its present luminosity would be (Tinsley, 1972; Worthey, 1994)

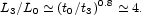(75)

If t_f were larger, but still less than t₃, this ratio would be larger. If t_f were greater than t₃ the galaxy would not be seen, absent earlier generations of stars. In a more realistic picture significant star formation may be distributed over a considerable range of redshifts, and the effect on the typical galaxy luminosity at a given redshift accordingly more complicated. Since there are many more galaxies with low luminosities than galaxies with high luminosities, one has to know the luminosity evolution quite well for a meaningful comparison of galaxy counts at high and low redshifts. The present situation is illustrated by the rather different indications from studies by Phillipps et al. (2000) and Totani et al. (2001).

The understanding of galaxy evolution and the interpretation of galaxy counts will be improved by large samples of counts of galaxies as a function of color, apparent magnitude, and redshift. Newman and Davis (2000) point to a promising alternative: count galaxies as a function of the internal velocity dispersion that in spirals correlates with the dispersion in the dark matter halo. That could eliminate the need to understand the evolution of star populations. There is still the issue of evolution of the dark halos by merging and accretion, but that might be reliably modeled by numerical simulations within the CDM picture. Either way, with further work galaxy counts may provide an important test for dark energy and its evolution (Newman and Davis, 2000; Huterer and Turner, 2001; Podariu and Ratra, 2001).

6. The gravitational lensing rate

The probability of production of multiple images of a quasar or a radio source by gravitational lensing by a foreground galaxy, or of strongly lensed images of a galaxy by a foreground cluster of galaxies, adds the relativistic expression for the deflection of light to the physics of the homogeneous cosmological model. Fukugita, Futamase, and Kasai (1990) and Turner (1990) point out the value of this test: at small _M0 the predicted lensing rate is considerably larger in a flat model with than in an open model with = 0 (as illustrated in Fig 13.12 in Peebles, 1993).

The measurement problem for the analysis of quasar lensing is that quasars that are not lensed are not magnified by lensing, making them harder to find and the correction for completeness of detection harder to establish. Present estimates (Falco, Kochanek, and Muñoz, 1998; Helbig et al., 1999) do not seriously constrain _M0 in an open model, and in a flat model (_K0 = 0) suggest _M0 > 0.36 at 2. This is close to the upper bound in Eq. (59). Earlier indications that the lensing rate in a flat model with constant requires a larger value of _M0 than is suggested by galaxy dynamics led Ratra and Quillen (1992) and Waga and Frieman (2000) to investigate the inverse power-law potential dark energy scalar field case. They showed this can significantly lower the predicted lensing rate at _K0 = 0 and small _M0. The lensing rate still is too uncertain to draw conclusions on this point, but advances in the measurement certainly will be followed with interest.

The main problem in the interpretation of the rate of strong lensing of galaxies by foreground clusters as a cosmological test is the sensitivity of the lensing cross section to the mass distribution within the cluster (Wu and Hammer, 1993); for the present still somewhat uncertain state of the art see Cooray (1999) and references therein.

7. Dynamics and the mean mass density

Estimates of the mean mass density from the relation between the mass distribution and the resulting peculiar velocities, ⁸¹ and from the gravitational deflection of light, probe gravity physics and constrain _M0. The former is not sensitive to _K0, ₀, or the dynamics of the dark energy, the latter only through the angular size distances.

We begin with the redshift space of observed galaxy angular positions and redshift distances z/H₀ in the radial direction. The redshift z has a contribution from the radial peculiar velocity, which is a probe of the gravitational acceleration produced by the inhomogeneous mass distribution. The two-point correlation function, _v, in redshift space is defined by the probability that a randomly chosen galaxy has a neighbor at distance r_|| along the line of sight in redshift space and perpendicular distance r,

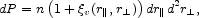(76)

where n is the galaxy number density. This is the usual definition of a reduced correlation function. Peculiar velocities make the function anisotropic. On small scales the random relative peculiar velocities of the galaxies broaden _v along the line of sight. On large scales the streaming peculiar velocity of convergence to gravitationally growing mass concentrations flattens _v along the line of sight. ⁸²

At 10 kpc hr 1 Mpc the measured line-of-sight broadening is prominent, and indicates the one-dimensional relative velocity dispersion is close to independent of r at ~ 300 km s^-1. ⁸³ This is about what would be expected if the mass two-and three-point correlation functions were well approximated by the galaxy correlation functions, the mass clustering on these scales were close to statistical equilibrium, and the density parameter were in the range of Eq. (59).

We have a check from the motions of the galaxies in and around the Local Group of galaxies, where the absolute errors in the measurements of galaxy distances are least. The two largest group members are the Andromeda Nebula (M 31) and our Milky Way galaxy. If they contain most of the mass their relative motion is the classical two-body problem in Newtonian mechanics (with minor corrections for , mass accretion at low redshifts, and the tidal torques from neighboring galaxies). The two galaxies are separated by 800 kpc and approaching at 110 km s^-1. In the minimum mass solution the galaxies have completed just over half an orbit in the cosmological expansion time t₀ ~ 10¹⁰ yr. By this argument Kahn and Woltjer (1959) find the sum of masses of the two galaxies has to be an order of magnitude larger than what is seen in the luminous parts. An extension to the analysis of the motions and distances of the galaxies within 4 Mpc distance from us, and taking account of the gravitational effects of the galaxies out to 20 Mpc distance, gives masses quite similar to what Kahn and Woltjer found, and consistent with _M0 in the range of Eq. (59) (Peebles et al., 2001).

We have another check from weak lensing: the shear distortion of images of distant galaxies by the gravitational deflection by the inhomogeneous mass distribution. ⁸⁴ If galaxies trace mass these measurements say the matter density parameter measured on scales from about 1 Mpc to 10 Mpc is in the range of Eq. (59). It will be interesting to see whether these measurements can check the factor of two difference between the relativistic gravitational deflection of light and the naive Newtonian deflection angle.

The redshift space correlation function _v (Eq. [76]) is measured well enough at hr ~ 10 Mpc to demonstrate the flattening effect, again consistent with _M0 in the range of Eq. (59), if galaxies trace mass. Similar numbers follow from galaxies selected as far infrared IRAS sources (Tadros et al., 1999) and from optically selected galaxies (Padilla et al., 2001; Peacock et al., 2001). The same physics, applied to estimates of the mean relative peculiar velocity of galaxies at separations ~ 10 Mpc, yet again indicates a similar density parameter (Juszkiewicz et al., 2000).

Other methods of analysis of the distributions of astronomical objects and peculiar velocities smoothed over scales 10 Mpc give a variety of results for the mass density, some above the range in Eq. (59), ⁸⁵ others towards the bottom end of the range (Branchini et al., 2001). The measurement of _M0 from large-scale streaming velocities thus remains open. But we are impressed by an apparently simple local situation, the peculiar motion of the Local Group toward the Virgo cluster of galaxies. This is the nearest known large mass concentration, at distance ~ 20 Mpc. Burstein (2000) finds that our virgocentric velocity is v_v = 220 km s^-1, indicating _M0 0.2 (Davis and Peebles, 1983a, Fig. 1). This leads us to conclude that the weight of the evidence from dynamics on scales ~ 10 Mpc favors low _M0, in the range of Eq. (59).

None of these measurements is precise. But many have been under discussion for a long time and seem to us to be reliably understood. Weak lensing is new, but the measurements are checked by several independent groups. The result, in our opinion, is a well checked and believable network of evidence that over two decades of well-sampled length scales, 100 kpc to 10 Mpc, the apparent value of _M0 is constant to a factor of three or so, in the range 0.15 _M0 0.4. The key point for the purpose of this review is that this result is contrary to what might have been expected from biasing, or from a failure of the inverse square law (as will be discussed in test [13]).

8. The baryon mass fraction in clusters of galaxies

Abell (1958) made the first useful catalog of the rich clusters considered here and in the next test. A typical value of the Abell cluster mass within the Abell radius r_a = 1.5 h^-1 Mpc is 3 × 10¹⁴ h^-1 M. The cluster masses are reliably measured (within Newtonian gravity) from consistent results from the velocities of the galaxies, the pressure of the intracluster plasma, and the gravitational deflection of light from background galaxies.

White (1992) and White et al. (1993) point out that rich clusters likely are large enough to contain a close to fair sample of baryons and dark matter, meaning the ratio of baryonic to total mass in a cluster is a good measure of _B0 / _M0. With _B0 from the model for light elements (Eqs. [62]), this gives a measure of the mean mass density. The baryon mass fraction in clusters is still under discussion. ⁸⁶ We adopt as the most direct and so maybe most reliable approach the measurement of the baryonic gas mass fraction of clusters, f_gas, through the Sunyaev-Zel'dovich microwave decrement caused by Thomson-Compton scattering of cosmic microwave background radiation by the intracluster plasma. The Carlstrom et al. (2001) value for f_gas gives _M0 ~ 0.25, ⁸⁷in the range of Eq. (59). This test does not directly constrain _K0, ₀, or the dynamics of the dark energy.

9. The cluster mass function

In the CDM model rich clusters of galaxies grow out of the rare peak upward fluctuations in the primeval Gaussian mass distribution. Within this model one can adjust the amplitude of the mass fluctuations to match the abundance of clusters at one epoch. In the Einstein-de Sitter model it is difficult to see how this one free adjustment can account for the abundance of rich clusters now and at redshifts near unity. ⁸⁸

Most authors now agree that the low density flat CDM model can give a reasonable fit to the cluster abundances as a function of redshift. The constraint on _M0 from the present cluster abundance still is under discussion, but generally is found to be close to _M0 ~ 0.3 if galaxies trace mass. ⁸⁹ The constraint from the evolution of the cluster number density also is under discussion. ⁹⁰ The predicted evolution is slower in a lower density universe, and at given _M0 the evolution is slower in an open model with = 0 than in a spatially-flat model with (for the reasons discussed in Sec. III.D). Bahcall and Fan (1998) emphasize that we have good evidence for the presence of some massive clusters at z ~ 1, and that this is exceedingly difficult to understand in the CDM model in the Einstein-de Sitter cosmology (when biasing is adjusted to get a reasonable present number density). Low density models with or without can account for the existence of some massive clusters at high redshift. Distinguishing between the predictions of the spatially curved and flat low density cases awaits better measurements.

10. Biasing and the development of nonlinear mass density fluctuations

Elements of the physics of cluster formation in test (9) appear in this test of the early stages in the nonlinear growth of departures from homogeneity. An initially Gaussian mass distribution becomes skew as low density fluctuations start to bottom out and high density fluctuations start to develop into prominent mass peaks. 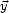The early signature of this nonlinear evolution is the disconnected three-point mass autocorrelation function, <(, t) (, t) (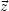, t)>, where (, t) = / is the dimensionless mass contrast. If galaxies are useful mass tracers the galaxy three-point function is a good measure of this mass function.

The form for the mass three-point function, for Gaussian initial conditions at high redshift, in lowest nonzero order in perturbation theory, is worked out in Fry (1984), and Fry (1994) makes the point that measurements of the galaxy three-point function test how well galaxies trace mass. ⁹¹ There are now two sets of measurements of the galaxy three-point function on scales ~ 10 to 20 Mpc, where the density fluctuations are not far from Gaussian. One uses infrared-selected IRAS galaxies, ⁹² the other optically-selected galaxies (Verde et al., 2002). The latter is consistent with the perturbative computation of the mass three-point function for Gaussian initial conditions. The former says infrared-selected galaxies are adequate mass tracers apart from the densest regions, which IRAS galaxies avoid. That has a simple interpretation in astrophysics: galaxies in dense regions tend to be swept clear of the gas and dust that make galaxies luminous in the infrared.

This test gives evidence of consistency of three ideas: galaxies are useful mass tracers on scales ~ 10 Mpc, the initial conditions are close to Gaussian, and conventional gravity physics gives an adequate description of this aspect of the growth of structure. It is in principle sensitive to ₀, through the suppression of the growth of small departures from homogeneity at low redshift, but the effect is small.

11. The anisotropy of the cosmic microwave background radiation

The wonderfully successful CDM prediction of the power spectrum of the angular distribution of the temperature of the 3 K cosmic microwave background radiation has converted many of the remaining skeptics in the cosmology community to the belief that the CDM model likely does capture important elements of reality.

Efstathiou (2002) provides a useful measure of the information in the present measurements ⁹³: the fit to the CDM model significantly constrains three linear combinations of the free parameters. We shall present three sets of considerations that roughly follow Efstathiou's constraints. We begin with reviews of the standard measure of the temperature anisotropy and of the conditions at redshift z ~ 1000 that are thought to produce the observed anisotropy.

The 3 K cosmic microwave background temperature T(, ) as a function of position in the sky usually is expressed as an expansion in spherical harmonics,

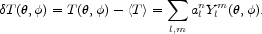(77)

The square of T averaged over the sky is

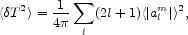(78)

where |a_l^m|² is statistically independent of m. This may be rewritten as

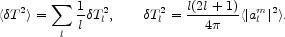(79)

Since l^-1 is close to d ln l, T_l² is the variance of the temperature per logarithmic interval of l. A measure of the angular scale belonging to the multipole index l is that the minimum distance between zeros of the spherical harmonic Y_l^m, in longitude or latitude, is = / l, except close to the poles, where Y_l^m approaches zero. ⁹⁴

Now let us consider the main elements of the physics that determines the 3 K cosmic microwave background anisotropy. ⁹⁵ At redshift z_dec ~ 1000 the temperature reaches the critical value at which the primeval plasma combines to atomic hydrogen (and slightly earlier to neutral helium). This removes the coupling between baryons and radiation by Thomson scattering, leaving the radiation to propagate nearly freely (apart from residual gravitational perturbations). Ratios of mass densities near the epoch z_dec when matter and radiation decouple are worth noting. At redshift z_eq = 2.4 × 10⁴ _M0 h² the mass density in matter -- including the baryonic and nonbaryonic components -- is equal to the relativistic mass density in radiation and neutrinos assumed to have low masses. At decoupling the ratio of mass densities is

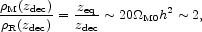(80)

at the central values of the parameters in Eqs. (6) and (59). The ratio of mass densities in baryons and in thermal cosmic microwave background radiation -- not counting neutrinos -- is

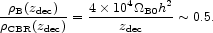(81)

That is, the baryons and radiation decouple just as the expansion rate has become dominated by nonrelativistic matter and the baryons are starting to lower the velocity of sound in the coupled baryon-radiation fluid (presenting us with still more cosmic coincidences).

The acoustic peaks in the spectrum of angular fluctuations of the 3 K cosmic microwave background radiation come from the Fourier modes of the coupled baryon-radiation fluid that have reached maximum or minimum amplitude at decoupling. Since all Fourier components start at zero amplitude at high redshift -- in the growing density perturbation mode -- this condition is

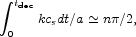(82)

where c_s is the velocity of sound in the baryon-radiation fluid. Before decoupling the mass density in radiation is greater than that of the baryons, so the velocity of sound is close to c / 3^1/2. The proper wavelength at the first acoustic peak thus is

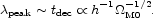(83)

The parameter dependence comes from Eq. (66). The observed angle subtended by _peak is set by the angular size distance r computed from z_eq to the present (Eq. [71]). If _K0 = 0 or ₀ = 0 the angular size distance is

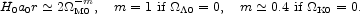(84)

If = 0 this expression is analytic at large z_eq. The expression for _K0 = 0 is a reasonable approximation to the numerical solution. So the angular scale of the peak varies with the matter density parameter as

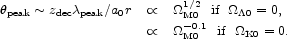(85) (86)

The key point from these considerations is that the angle defined by the first peak in the fluctuation power spectrum is sensitive to _M0 if = 0 (Eq. [85]), but not if _K0 = 0 (Eq. [86]). ⁹⁶ We have ignored the sensitivity of z_dec and t_dec to _M0, but the effect is weak. More detailed computations, which are needed for a precise comparison with the data, show that the CDM model predicts that the first and largest peak of T_l appears at multipole index l_peak 220 _M0^-1/2 if = 0, and at l_peak 220 if _K0 = 0 and 0.1 _M0 1. ⁹⁷

The measured spectrum ⁹⁸ peaks at T_l ~ 80 µK at l ~ 200, thus requiring small space curvature in the CDM model. This is the first of Efstathiou's constraints. Because of the geometric degeneracy this measurement does not yet seriously constrain _M0 if _K0 = 0.

The second constraint comes from the spectrum of temperature fluctuations on large scales, l 30, where pressure gradient forces never were very important. Under the scale-invariant initial conditions discussed in Sec. III.C the Einstein-de Sitter model predicts T_l is nearly independent of l on large scales. A spatially-flat model with _M0 ~ 0.3, predicts T_l decreases slowly with increasing l at small l. ⁹⁹ The measured spectrum is close to flat at T_l ~ 30 µK, but not well enough constrained for a useful measure of the parameters _M0 and ₀. ¹⁰⁰ Because of the simplicity of the physics on large angular scales, this provides the most direct and so perhaps most reliable normalization of the CDM model power spectrum (that is, the parameter A in Eqs. [40] and [41]).

The third constraint is the baryon mass density. It affects the speed of sound c_s (Eq. [82]) in the baryon-radiation fluid prior to decoupling, and the mean free path for the radiation at z ~ z_dec. These in turn affect the predicted sequence of acoustic peaks (see, e.g., Hu and Sugiyama, 1996). The detected peaks are consistent with a value for the baryon density parameter _B0 in a range that includes what is derived from the light elements abundances (Eqs. [62]). ¹⁰¹ This impressive check may be much improved by the measurements of T_l in progress.

The measurements of T_l are consistent with a near scale-invariant power spectrum (Eq. [41] with n 1) with negligible contribution from gravity wave or isocurvature fluctuations (Sec. III.C.1). The 3 K cosmic microwave background temperature fluctuations show no departure from a Gaussian random process. ¹⁰² This agrees with the picture in test (10) for the nonlinear growth of structure out of Gaussian initial mass density fluctuations.

The interpretation of the cosmic microwave background temperature anisotropy measurements assumes and tests general relativity and the CDM model. One can write down other models for structure formation that put the peak of T_l at about the observed angular scale -- an example is Hu and Peebles (2000) -- but we have seen none so far that seem likely to fit the present measurements of T_l. Delayed recombination of the primeval plasma in an low density = 0 CDM model can shift the peak of T_l to the observed scale. ¹⁰³ The physics is valid, but the scenario is speculative and arguably quite improbable. On the other hand, we cannot be sure a fix of the challenges to CDM reviewed in Sec. IV.A.2 will not affect our assessments of such issues, and hence of this cosmological test.

12. The mass autocorrelation function and nonbaryonic matter

If the bulk of the nonrelativistic matter, with density parameter _M0 ~ 0.25, were baryonic, then under adiabatic initial conditions the most immediate problem would be the strong dissipation of primeval mass density fluctuations on the scale of galaxies by diffusion of radiation through the baryons at redshifts near decoupling. ¹⁰⁴ Galaxies could form by fragmentation of the first generation of protocluster "pancakes," as Zel'dovich (1978) proposed, but this picture is seriously challenged by the evidence that the galaxies formed before clusters of galaxies. ¹⁰⁵ In a baryonic dark matter model we could accommodate the observations of galaxies already present at z ~ 3 by tilting the primeval mass fluctuation spectrum to favor large fluctuations on small scales, but that would mess up the cosmic microwave background anisotropy. The search for isocurvature initial conditions that might fit both in a baryonic dark matter model has borne no fruit so far (Peebles, 1987).

The most important point of this test is the great difficulty of reconciling the power spectra of matter and radiation without the postulate of nonbaryonic dark matter. The CDM model allows hierarchical growth of structure, from galaxies up, which is what seems to be observed, because the nonbaryonic dark matter interacts with baryons and radiation only by gravity; the dark matter distribution is not smoothed by the dissipation of density fluctuations in the baryon-radiation fluid at redshifts z z_eq.

As discussed in Sec. III.D, in the CDM model the small scale part of the dark matter power spectrum bends from the primeval scale-invariant form P(k) k to P(k) k^-3, and the characteristic length at the break scales inversely with _M0 (Eq. [42]). Evidence of such a break in the galaxy power spectrum P_g(k) has been known for more than a decade ¹⁰⁶; it is consistent with a value of _M0 in the range of Eq. (59).

13. The gravitational inverse square law

The inverse square law for gravity determines the relation between the mass distribution and the gravitationally-driven peculiar velocities that enter estimates of the matter density parameter _M0. The peculiar velocities also figure in the evolution of the mass distribution, and hence the relation between the present mass fluctuation spectrum and the spectrum of cosmic microwave background temperature fluctuations imprinted at redshift z ~ 1000. We are starting to see demanding tests of both aspects of the inverse square law.

We have a reasonably well checked set of measurements of the apparent value of _M0 on scales ranging from 100 kpc to 10 Mpc (as reviewed under test [7]). Most agree with a constant value of the apparent _M0, within a factor of three or so. This is not the precision one would like, but the subject has been under discussion for a long time, and, we believe, is now pretty reliably understood, within the factor of three or so. If galaxies were biased tracers of mass one might have expected to have seen that _M0 increases with increasing length scale, as the increasing scale includes the outer parts of extended massive halos. Maybe that is masked by a gravitational force law that decreases more rapidly than the inverse square law at large distance. But the much more straightforward reading is that the slow variation of _M0 sampled over two orders of magnitude in length scale agrees with the evidence from tests (7) to (10) that galaxies are useful mass tracers, and that the inverse square law therefore is a useful approximation on these scales.

The toy model in Eq. (57) illustrates how a failure of the inverse square law would affect the evolution of the shape of the mass fluctuation power spectrum P(k, t) as a function of the comoving wavenumber k, in linear perturbation theory. This is tested by the measurements of the mass and cosmic microwave background temperature fluctuation power spectra. The galaxy power spectrum P_g(k) varies with wavenumber at k ~ 0.1h Mpc^-1 about as expected under the assumptions that the mass distribution grew by gravity out of adiabatic scale-invariant initial conditions, the mass is dominated by dark matter that does not suffer radiation drag at high redshift, the galaxies are useful tracers of the present mass distribution, the matter density parameter is _M0 ~ 0.3, and, of course, the evolution is adequately described by conventional physics (Hamilton and Tegmark, 2002, and references therein). If the inverse square law were significantly wrong at k ~ 0.1h Mpc^-1, the near scale-invariant form would have to be an accidental effect of some failure in this rather long list of assumptions. This seems unlikely, but a check certainly is desirable. We have one, from the cosmic microwave background anisotropy measurements. They also are consistent with near scale-invariant initial conditions applied at redshift z ~ 1000. This preliminary check on the effect of the gravitational inverse square law applied on cosmological length scales and back to redshift z ~ 1000 will be improved by better understanding of the effect on T_l of primeval tensor perturbations to spacetime, and of the dynamical response of the dark energy distribution to the large-scale mass distribution.

Another aspect of this check is the comparison of values of the large-scale rms fluctuations in the present distributions of mass and the cosmic microwave background radiation. The latter is largely set at decoupling, after which the former grows by a factor of about 10³ to the present epoch, in the standard relativistic cosmological model. If space curvature is negligible the growth factor agrees with the observations to about 30%, assuming galaxies trace mass. In a low density universe with = 0 the standard model requires that mass is more smoothly distributed than galaxies, N / N ~ 3M / M, or that the gravitational growth factor since decoupling is a factor of three off the predicted factor ~ 1000; this factor of three is about as large a deviation from unity as is viable. We are not proposing this interpretation of the data, rather we are impressed by the modest size of the allowed adjustment to the inverse square law.

⁷⁰ This was recognized by Zel'dovich (1964), R. Feynman, in 1964, and S. Refsdal, in 1965. Feynman's comments in a colloquium are noted by Gunn (1967). Peebles attended Refsdal's lecture at the International Conference on General Relativity and Gravitation, London, July 1965; Refsdal (1970) mentions the lecture. Back.

⁷¹ The history of the discovery and measurement of this radiation, and its relation to the light element abundances in test (2), is presented in Peebles (1971, pp. 121-9 and 240-1), Wilkinson and Peebles (1990), and Alpher and Herman (2001). The precision spectrum measurements are summarized in Halpern, Gush, and Wishnow (1991) and Fixsen et al. (1996). Back.

⁷² To see this, recall the normal modes argument used to get Eq. (7). The occupation number in a normal mode with wavelength at temperature T is the Planck form = [e ^{c / kT} - 1]^-1. Adiabaticity says is constant. Since the mode wavelength varies as a(t), where a is the expansion factor in Eq. (4), and is close to constant, the mode temperature varies as T 1 / a(t). Since the same temperature scaling applies to each mode, an initially thermal sea of radiation remains thermal in the absence of interactions. We do not know the provenance of this argument; it was familiar in Dicke's group when the 3 K cosmic microwave background radiation was discovered. Back.

⁷³ There is a long history of discussions of this probe of the expansion rate at the redshifts of light element production. The reduction of the helium abundance to Y ~ 0.2 if the expansion time is increased by the factor 2^1/2 is seen in Figs. 1 and 2 in Peebles (1966). Dicke (1968) introduced the constraint on evolution of the strength of the gravitational interaction; see Uzan (2002) for a recent review. The effect of the number of neutrino families on the expansion rate and hence the helium abundance is noted by Hoyle and Tayler (1964) and Shvartsman (1969). Steigman, Schramm, and Gunn (1977) discuss the importance of this effect as a test of cosmology and of the particle physics measures of the number of neutrino families. Back.

⁷⁴ The predicted maximum age of star populations in galaxies at redshifts z 1 does still depend on ₀ and _K0, and there is the advantage that the predicted maximum age is a lot shorter than today. This variant of the expansion time test is discussed by Nolan et al. (2001), Lima and Alcaniz (2001), and references therein. Back.

⁷⁵ See Carretta et al. (2000), Krauss and Chaboyer (2001), Chaboyer and Krauss (2002), and references therein. Back.

⁷⁶ The earliest discussion we know of the magnification effect is by Hoyle (1959). In the coordinate system in Eq. (15), with the observer at the origin, light rays from the object move to the observer along straight radial lines. An image at high redshift is magnified because the light detected by the observer is emitted when the proper distance to the object measured at fixed world time is small. Because the proper distance between the object and source is increasing faster than the speed of light, emitted light directed at the observer is initially moving away from the observer. Back.

⁷⁷ For a review of measurements of the redshift-magnitude relation (and other cosmological tests) we recommend Sandage (1988). A recent application to the most luminous galaxies in clusters is in Aragón-Salamanca, Baugh, and Kauffmann (1998). The redshift-angular size relation is measured by Daly and Guerra (2001) for radio galaxies, Buchalter et al. (1998) for quasars, and Gurvits, Kellermann, and Frey (1999) for compact radio sources. Constraints on the cosmological parameters from the Gurvits et al. data are discussed by Vishwakarma (2001), Lima and Alcaniz (2002), Chen and Ratra (2003), and references therein, and constraints based on the radio galaxy data are discussed by Daly and Guerra (2001), Podariu et al. (2003), and references therein. Back.

⁷⁸ These supernovae are characterized by the absence of hydrogen lines in the spectra; they are thought to be the result of explosive nuclear burning of white dwarf stars. Pskovskii (1977) and Phillips (1993) pioneered the reduction of the supernovae luminosities to a near universal standard candle. For recent discussions of their use as a cosmological test see Goobar and Perlmutter (1995), Reiss et al. (1998), Perlmutter et al. (1999a), Gott et al. (2001), and Leibundgut (2001). We recommend Leibundgut's (2001) cautionary discussion of astrophysical uncertainties: the unknown nature of the trigger for the nuclear burning, the possibility that the Phillips correction to a fiducial luminosity actually depends on redshift or environment within a galaxy, and possible obscuration by intergalactic dust. There are also issues of physics that may affect this test (and others): the strengths of the gravitational or electromagnetic interactions may vary with time, and photon-axion conversion may reduce the number of photons reaching us. All of this is under active study. Back.

⁷⁹ Podariu and Ratra (2000) and Waga and Frieman (2000) discuss the redshift-magnitude relation in the inverse power-law scalar field model, and Waga and Frieman (2000) and Ng and Wiltshire (2001) discuss this relation in the massive scalar field model. Back.

⁸⁰ Podariu, Nugent, and Ratra (2001), Weller and Albrecht (2002), Wang and Lovelace (2001), Gerke and Efstathiou (2002), Eriksson and Amanullah (2002), and references therein, discuss constraints on cosmological parameters from the proposed SNAP mission. Back.

⁸¹ Early estimates of the mean mass density, by Hubble (1936, p. 189) and Oort (1958), combine the galaxy number density from galaxy counts with estimates of galaxy masses from the internal motions of gas and stars. Hubble (1936, p. 180) was quite aware that this misses mass between the galaxies, and that the motions of galaxies within clusters suggests there is a lot more intergalactic mass (Zwicky, 1933; Smith, 1936). For a recent review of this subject see Bahcall et. al. (2000). Back.

⁸² This approach grew out of the statistical method introduced by Geller and Peebles (1973); it is derived in its present form in Peebles (1980b) and first applied to a serious redshift sample in Davis and Peebles (1983b). These references give the theory for the second moment ² of _v in the radial direction -- the mean square relative peculiar velocity -- in the small-scale stable clustering limit. The analysis of the anisotropy of _v in the linear perturbation theory of large-scale flows (Eq. [55]) is presented in Kaiser (1987). Back.

⁸³ This measurement requires close attention to clusters that contribute little to the mean mass density but a broad and difficult to measure tail to the distribution of relative velocities. Details may be traced back through Padilla et al. (2001), Peacock et al. (2001), and Landy (2002). Back.

⁸⁴ Recent studies include Wilson, Kaiser, and Luppino (2001), Van Waerbeke et al. (2002), Refregier, Rhodes, and Groth (2002), Bacon et al. (2002), and Hoekstra, Yee, and Gladders (2002). See Munshi and Wang (2002) and references therein for discussions of how weak lensing might probe dark energy. Back.

⁸⁵ The methods and results may be traced through Fisher, Scharf, and Lahav (1994), Sigad et al. (1998), and Branchini et al. (2000). Back.

⁸⁶ See Hradecky et al. (2000), Roussel, Sadat, and Blanchard (2000), Allen, Schmidt, and Fabian (2002), and references therein. Back.

⁸⁷ This assumes _B0 h² = 0.014 from Eqs. (62). For the full range of values in Eqs. (6) and (62), 0.1 _M0 0.4 at two standard deviations. Back.

⁸⁸ Early discussions of this problem include Evrard (1989), Peebles, Daly, and Juszkiewicz (1989), and Oukbir and Blanchard (1992). Back.

⁸⁹ For recent discussions see Pierpaoli, Scott, and White (2001), Seljak (2001), Viana, Nichol, and Liddle (2002), Ikebe et al. (2002), Bahcall et al. (2002), and references therein. Wang and Steinhardt (1998) consider this test in the context of the XCDM parametrization; to our knowledge it has not been studied in the scalar field dark energy case. Back.

⁹⁰ Examples include Blanchard et al. (2000), and Borgani et al. (2001). Back.

⁹¹ Other notable contributions to the development of this point include Bernardeau and Schaeffer (1992), Fry and Gaztañaga (1993), and Hivon et al. (1995). Back.

⁹² Two sub-samples of IRAS galaxies are analyzed by Scoccimarro et al. (2001) and by Feldman et al. (2001). Back.

⁹³ Recent measurements are presented in Lee et al. (2001), Netterfield et al. (2002), Halverson et al. (2002), Miller et al. (2002a), Coble et al. (2001), Scott et al. (2002), and Mason et al. (2002). Back.

⁹⁴ A more careful analysis distinguishes averages across the sky from ensemble averages. By historical accident the conventional normalization replaces 2l + 1 with 2(l + 1) in Eq. (79). Kosowsky (2002) reviews the physics of the polarization of the radiation. Back.

⁹⁵ The physics is worked out in Peebles and Yu (1970) and Peebles (1982). Important analytic considerations are in Sunyaev and Zel'dovich (1970). The relation of the cosmic microwave background anisotropy to the cosmological parameters is explored in many papers; examples of the development of ideas include Bond (1988), Bond et al. (1994), Hu and Sugiyama (1996), Ratra et al. (1997, 1999), Zaldarriaga, Spergel, and Seljak (1997), and references therein. Back.

⁹⁶ This "geometrical degeneracy" is discussed by Efstathiou and Bond (1999). Marriage (2002) presents a closer analysis of the effect. Sugiyama and Gouda (1992), Kamionkowski, Spergel, and Sugiyama (1994b), and Kamionkowski et al. (1994a) are early discussions of the cosmic microwave background anisotropy in an open model. Back.

⁹⁷ Brax et al. (2000) and Baccigalupi et al. (2000) compute the angular spectrum of the cosmic microwave background anisotropy in the dark energy scalar field model. Doran et al. (2001) discuss the angular scale of the peaks in this case, and Corasaniti and Copeland (2002), Baccigalupi et al. (2002), and references therein, compare model predictions and observations -- it is too early to draw profound conclusions about model viability, and new data are eagerly anticipated. Wasserman (2002) notes that the cosmic microwave background anisotropy data could help discriminate between different dark energy scalar field models whose predictions do not differ significantly at low redshift. Back.

⁹⁸ For analyses see Knox and Page (2000), Podariu et al. (2001), Wang, Tegmark, and Zaldarriaga (2002), Durrer, Novosyadlyj, and Apunevych (2002), Miller et al. (2002b), and references therein. Back.

⁹⁹ The physics was first demonstrated by Sachs and Wolfe (1967) and applied in the modern context by Peebles (1982). The intermediate Sachs-Wolfe effect that applies if the universe is not Einstein-de Sitter is shown in Eq. (93.26) in Peebles (1980). This part of the Sachs-Wolfe effect receives a contribution from the low redshift matter distribution, so cross-correlating the observed large-scale cosmic microwave background anisotropy with the low redshift matter distribution could provide another test of the world model (Boughn and Crittenden, 2001, and references therein). Back.

¹⁰⁰ See, e.g., Górski et al. (1998). This ignores the "low" value of the cosmological quadrupole (l = 2) moment, whose value depends on the model used to remove foreground Galactic emission (see, e.g., Kogut et al., 1996). Contamination due to non-cosmic microwave background emission is an issue for some of the anisotropy data sets (see, e.g., de Oliveira-Costa et al., 1998; Hamilton and Ganga, 2001; Mukherjee et al., 2002, and references therein). Other issues that need care in such analyses include accounting for the uncertainty in the calibration of the experiment (see, e.g., Ganga et al., 1997; Bridle et al., 2002), and accounting for the shape of the antenna pattern (see, e.g., Wu et al., 2001a; Souradeep and Ratra, 2001; Fosalba, Dore, and Bouchet, 2002). Back.

¹⁰¹ The _B0 h² values estimated from the cosmic microwave background anisotropy measured by Netterfield et al. (2002), Pryke et al. (2002), and Stompor et al. (2001), are more consistent with the higher, deuterium based, Burles et al. (2001) range in Eqs. (62). Back.

¹⁰² Colley, Gott, and Park (1996) present an early discussion of the situation on large angular scales; more recent discussions are in Mukherjee, Hobson, and Lasenby (2000), Phillips and Kogut (2001), and Komatsu et al. (2002). Degree and sub-degree angular scale anisotropy data are studied in Park et al. (2001), Wu et al. (2001b), Shandarin et al. (2002), and Polenta et al. (2002). Back.

¹⁰³ The model in Peebles, Seager, and Hu (2000) assumes stellar ionizing radiation at z ~ 1000 produces recombination Lyman photons. These resonance photons promote photoionization from the n = 2 level of atomic hydrogen. That allows delayed recombination with a rapid transition to neutral atomic hydrogen, as required to get the shape of T_l about right. Back.

¹⁰⁴ Early analyses of this effect are in Peebles (1965), and Silk (1967, 1968). Back.

¹⁰⁵ For example, our Milky Way galaxy is in the Local Group, which seems to be just forming, because the time for a group member to cross the Local Group is comparable to the Hubble time. The Local Group is on the outskirts of the concentration of galaxies around the Virgo cluster. We and neighboring galaxies are moving away from the cluster, but at about 80 percent of the mean Hubble flow, as if the local mass concentration were slowing the local expansion. That is, our galaxy, which is old, is starting to cluster with other galaxies, in a "bottom up" hierarchical growth of structure, as opposed to the "top down" evolution of the pancake picture. Back.

¹⁰⁶ The first good evidence is discussed in Efstathiou et al. (1990); for recent examples see Sutherland et al. (1999), Percival et al. (2001), and Dodelson et al. (2002). Back.