


D. The cold dark matter model
Some of the present cosmological tests were understood in the 1930s; others are based on new ideas about structure formation. A decade ago a half dozen models for structure formation were under discussion 38; now the known viable models have been winnowed to one class: cold dark matter (CDM) and variants. We comment on the present state of tests of the CDM model in Sec. IV.A.2, and in connection with the cosmological tests in Sec. IV.B.
The CDM model assumes the mass of the universe now is dominated by dark matter that is nonbaryonic and acts like a gas of massive, weakly interacting particles with negligibly small primeval velocity dispersion. Structure is supposed to have formed by the gravitational growth of primeval departures from homogeneity that are adiabatic, scale-invariant, and Gaussian. The early discussions also assume an Einstein-de Sitter universe. These features all are naturally implemented in simple models for inflation, and the CDM model may have been inspired in part by the developing ideas of inflation. But the motivation in writing down this model was to find a simple way to show that the observed present-day mass fluctuations can agree with the growing evidence that the anisotropy of the 3 K thermal cosmic microwave background radiation is very small (Peebles, 1982). The first steps toward turning this picture into a model for structure formation were taken by Blumenthal et al. (1984).
In the decade commencing about 1985 the standard cosmology for many active in research in this subject was the Einstein-de Sitter model, and for good reason: it eliminates the coincidences problem, it avoids the curiosity of nonzero dark energy, and it fits the condition from conventional inflation that space sections have zero curvature. But unease about the astronomical problems with the high mass density of the Einstein-de Sitter model led to occasional discussions of a low density universe with or without a cosmological constant, and the CDM model played an important role in these considerations, as we now discuss.
When the CDM model was introduced it was known that the observations disfavor the high mass density of the Einstein-de Sitter model, unless the mass is more smoothly distributed than the visible matter (Sec. III.C). The key papers showing that this wanted biased distribution of visible galaxies relative to the distribution of all of the mass can follow in a natural way in the CDM theory are Kaiser (1984) and Davis et al. (1985). In short, where the mass density is high enough to lead to the gravitational assembly of a large galaxy the mass density tends to be high nearby, favoring the formation of neighboring large galaxies
The biasing concept is important and certainly had to be
explored. But in 1985 there was little empirical evidence for the
effect and there were significant arguments against it, mainly
the empty state of the voids between the concentrations of large
galaxies. 39
In the biasing picture the voids contain most of the mass of an
Einstein-de Sitter universe, but few of the galaxies, because
galaxy formation there is supposed to have been suppressed. But
it is hard to see how galaxy formation could be entirely
extinguished: the CDM model would be expected to predict a void
population of irregular galaxies, that show signs of a difficult
youth. Many irregular galaxies are observed, but they avoid the
voids. The straightforward reading of the observations thus is
that the voids are empty, and that the dynamics of the motions
of the visible galaxies therefore say
 M0 is
well below unity, and that the mass is not more smoothly distributed
than the visible galaxies.
M0 is
well below unity, and that the mass is not more smoothly distributed
than the visible galaxies.
In a low density open universe, with

 0 =
0 and positive
0 =
0 and positive
 K0,
the growth of mass clustering is suppressed at
z
K0,
the growth of mass clustering is suppressed at
z 
 M0-1 - 1. Thus to agree with the
observed low redshift mass
distribution density fluctuations at high redshift must be larger
in the open model than in the Einstein-de Sitter case. This
makes it harder to understand the small 3 K cosmic microwave
background anisotropy. In a low density spatially-flat universe with
M0-1 - 1. Thus to agree with the
observed low redshift mass
distribution density fluctuations at high redshift must be larger
in the open model than in the Einstein-de Sitter case. This
makes it harder to understand the small 3 K cosmic microwave
background anisotropy. In a low density spatially-flat universe with
 K0 = 0
and a cosmological constant, the transition from
matter-dominated expansion to
K0 = 0
and a cosmological constant, the transition from
matter-dominated expansion to
 -dominated
expansion is more recent than the transition from matter-dominated expansion
to space-curvature-dominated expansion in an open universe with
-dominated
expansion is more recent than the transition from matter-dominated expansion
to space-curvature-dominated expansion in an open universe with
 = 0 , as one sees
from Eq. (11). This makes density fluctuations grow almost as
much as in the Einstein-de Sitter model, thus allowing smaller
peculiar velocities in the
flat-
= 0 , as one sees
from Eq. (11). This makes density fluctuations grow almost as
much as in the Einstein-de Sitter model, thus allowing smaller
peculiar velocities in the
flat- case, a big
help in understanding the observations.
40
case, a big
help in understanding the observations.
40
An argument for low
 M0, with
or without
M0, with
or without
 , developed
out of the characteristic length scale for structure in the CDM model.
In the Friedmann-Lemaître cosmology the mass distribution is
gravitationally unstable. This simple statement has a profound
implication: the early universe has to have been very close to
homogeneous, and the growing departures from homogeneity at high
redshift are well described by
linear perturbation theory. The linear density fluctuations may
be decomposed into Fourier components (or generalizations for
open or closed space sections). At high enough redshift the
wavelength of a mode is much longer than the time-dependent
Hubble length H-1, and gravitational instability makes
the mode amplitude grow. Adiabatic fluctuations remain adiabatic,
because different regions behave as if they were parts of
different homogeneous universes. When the Hubble length becomes
comparable to the mode proper wavelength, the baryons
and radiation, strongly coupled by Thomson scattering at high
redshift, oscillate as an
acoustic wave and the mode amplitude for the cold dark matter stops
growing. 41
The mass densities in dark matter and radiation are equal at
redshift zeq = 2.4 × 104
, developed
out of the characteristic length scale for structure in the CDM model.
In the Friedmann-Lemaître cosmology the mass distribution is
gravitationally unstable. This simple statement has a profound
implication: the early universe has to have been very close to
homogeneous, and the growing departures from homogeneity at high
redshift are well described by
linear perturbation theory. The linear density fluctuations may
be decomposed into Fourier components (or generalizations for
open or closed space sections). At high enough redshift the
wavelength of a mode is much longer than the time-dependent
Hubble length H-1, and gravitational instability makes
the mode amplitude grow. Adiabatic fluctuations remain adiabatic,
because different regions behave as if they were parts of
different homogeneous universes. When the Hubble length becomes
comparable to the mode proper wavelength, the baryons
and radiation, strongly coupled by Thomson scattering at high
redshift, oscillate as an
acoustic wave and the mode amplitude for the cold dark matter stops
growing. 41
The mass densities in dark matter and radiation are equal at
redshift zeq = 2.4 × 104
 M0
h2; thereafter the dark
matter mass density dominates and the fluctuations in its
distribution start to grow again. The suppressed growth of
density fluctuations within the Hubble length at
z > zeq produces a bend in the power
spectrum of the dark mass distribution, from
P(k)
M0
h2; thereafter the dark
matter mass density dominates and the fluctuations in its
distribution start to grow again. The suppressed growth of
density fluctuations within the Hubble length at
z > zeq produces a bend in the power
spectrum of the dark mass distribution, from
P(k)  k at long wavelengths, if scale-invariant (Eq. [40]), to
P(k)
k at long wavelengths, if scale-invariant (Eq. [40]), to
P(k)  k-3 at
short wavelengths. 42
This means that at small scales (large k) the contribution to the
variance of the mass density per logarithmic interval of
wavelength is constant, and at small k the contribution to the
variance of the Newtonian gravitational potential per logarithmic
interval of k is constant.
k-3 at
short wavelengths. 42
This means that at small scales (large k) the contribution to the
variance of the mass density per logarithmic interval of
wavelength is constant, and at small k the contribution to the
variance of the Newtonian gravitational potential per logarithmic
interval of k is constant.
The wavelength at the break in the spectrum is set by the Hubble
length at equal radiation and matter mass densities,
teq  zeq-2. This characteristic break
scale grows by the factor zeq to
zeq-2. This characteristic break
scale grows by the factor zeq to
 break ~
zeq teq at the present
epoch. The numerical value is
(Peebles, 1980a,
Eq. [92.47])
break ~
zeq teq at the present
epoch. The numerical value is
(Peebles, 1980a,
Eq. [92.47])
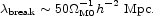 |
(42) |
If  is close to
constant, or
is close to
constant, or
 = 0 and space
sections are curved, it does not appreciably affect
the expansion rate at redshift zeq, so this
characteristic length is the same in flat and open cosmological
models. In an Einstein-de Sitter model, with
= 0 and space
sections are curved, it does not appreciably affect
the expansion rate at redshift zeq, so this
characteristic length is the same in flat and open cosmological
models. In an Einstein-de Sitter model, with
 M0 = 1,
the predicted length scale at the break in the power spectrum of
CDM mass fluctuations is uncomfortably small relative to
structures such as are observed in clusters of clusters of galaxies
(superclusters), and relative to the measured galaxy two-point
correlation function. That is, more power is observed on scales
~ 100 Mpc than is predicted in the CDM model with
M0 = 1,
the predicted length scale at the break in the power spectrum of
CDM mass fluctuations is uncomfortably small relative to
structures such as are observed in clusters of clusters of galaxies
(superclusters), and relative to the measured galaxy two-point
correlation function. That is, more power is observed on scales
~ 100 Mpc than is predicted in the CDM model with
 M0 = 1.
Since
M0 = 1.
Since  break
scales as
break
scales as  M0-1, a remedy is to go to a universe
with small
M0-1, a remedy is to go to a universe
with small
 M0,
either with
M0,
either with  = 0
and open space sections or
= 0
and open space sections or
 K0 = 0
and a nonzero cosmological constant. The latter case
is now known as
K0 = 0
and a nonzero cosmological constant. The latter case
is now known as  CDM.
43
CDM.
43
38 A scorecard is given in Peebles and Silk (1990). Structure formation models that assume all matter is baryonic, and those that augment baryons with hot dark matter such as low mass neutrinos, were already seriously challenged a decade ago. Vittorio and Silk (1985) show that the Uson and Wilkinson (1984) bound on the small-scale anisotropy of the 3 K cosmic microwave background temperature rules out a baryon-dominated universe with adiabatic initial conditions. This is because the dissipation of the baryon density fluctuations by radiation drag as the primeval plasma combines to neutral hydrogen (at redshift z ~ 1000) unacceptably suppresses structure formation on the scale of galaxies. Cold dark matter avoids this problem by eliminating radiation drag. This is one of the reasons attention turned to the hypothetical nonbaryonic cold dark matter. There has not been a thorough search for more baroque initial conditions that might save the baryonic dark matter model, however. Back.
39 The issue is presented in Peebles (1986); the data and history of ideas are reviewed in Peebles (2001). Back.
40 The demonstration that the suppression of peculiar velocities is a lot stronger than the suppression of the growth of structure is in Peebles (1984) and Lahav et al. (1991). Back.
41 At high redshift the dark matter mass density is less than that of the radiation. The radiation thus fixes the expansion rate, which is too rapid for the self-gravity of the dark matter to have any effect on its distribution. Early discussions of this effect are in Guyot and Zel'dovich (1970) and Mészáros (1972). Back.
42 That is, the transfer function in
Eq. (40) goes from
a constant at small k to T2(k)
 k-4
at large k.
Back.
k-4
at large k.
Back.
43 The scaling of
 break with
break with
 M0
was frequently noted in the 1980s. The earliest discussions
we have seen of the significance for large-scale structure are in
Silk and Vittorio (1987)
and Efstathiou,
Sutherland, and Maddox (1990),
who consider a spatially-flat universe,
Blumenthal, Dekel, and
Primack (1988),
who consider the open case, and
Holtzman (1989),
who considers both.
For the development of tests of the open case see
Lyth and Stewart (1990),
Ratra and Peebles
(1994),
Kamionkowski et
al. (1994a),
and Górski et
al. (1995).
Pioneering steps in the analysis of the anisotropy of the 3 K cosmic
microwave background temperature
in the
M0
was frequently noted in the 1980s. The earliest discussions
we have seen of the significance for large-scale structure are in
Silk and Vittorio (1987)
and Efstathiou,
Sutherland, and Maddox (1990),
who consider a spatially-flat universe,
Blumenthal, Dekel, and
Primack (1988),
who consider the open case, and
Holtzman (1989),
who considers both.
For the development of tests of the open case see
Lyth and Stewart (1990),
Ratra and Peebles
(1994),
Kamionkowski et
al. (1994a),
and Górski et
al. (1995).
Pioneering steps in the analysis of the anisotropy of the 3 K cosmic
microwave background temperature
in the  CDM model
include
Kofman and Starobinsky
(1985) and
Górski, Silk, and
Vittorio (1992).
We review developments after the COBE detection of the anisotropy
(Smoot et al., 1992)
in Secs. IV.B.11 and
12.
Back.
CDM model
include
Kofman and Starobinsky
(1985) and
Górski, Silk, and
Vittorio (1992).
We review developments after the COBE detection of the anisotropy
(Smoot et al., 1992)
in Secs. IV.B.11 and
12.
Back.