2. VIEW FROM THE INSIDE: DIVING INTO THE PHYSICS OF THE WARM IONIZED MEDIUM IN OUR GALAXY

2.1. Basic characteristics of the WIM and diagnostic tools

Our location within the disk of the Galaxy provides an opportunity to explore close up and in detail the distribution and physical properties of this ionized medium, including its ionization state and temperature. The basic features of the WIM are not very different from those first proposed by Hoyle and Ellis (1963). Temperatures range from about 6000 K to 10 000 K, and in the solar neighborhood, its average hydrogen ionization rate is approximately 4 × 10⁶ s^-1 within a one cm² column extending perpendicular through the Galactic disk, about 1/8th that available from stellar ionizing photons (e.g., Madsen et al. 2006, Reynolds 1984). The amount of ionization increases toward the Galactic center (e.g., Madsen and Reynolds 2005). In other galaxies, the average ionization rate is observed to be about 1/2 that available from the stars (see Section 4).

Two fundamental parameters of ionized gas along any line of sight, s, are the dispersion measures (DM n_e ds), derived from pulsar observations, and the emission measure (EM n_e n_H⁺ ds n_e² ds), derived from the intensity of the hydrogen Balmer-alpha (H) recombination line or from the amount of free-free (Bremsstrahlung) emission or absorption. Comparison of these measurements along common lines of sight indicate that the H⁺ is clumped into regions having an average electron density, n_e = 0.03-0.08 cm^-3, and filling a fraction, f 0.4-0.2, of the volume within a 2000-3000 pc thick layer about the Galactic midplane (Hill et al. 2008, Reynolds 1991b). Data also suggest that the filling fraction increases from f ~ 0.1 at the midplane to f > 0.3-0.4 at |z| = 1000 pc (Kulkarni and Heiles 1987, Reynolds 1991b, Gaensler et al. 2008, Berkhuijsen et al. 2006). The large, 1000-1800 pc scale height, significantly larger than that of the neutral hydrogen layer, has been deduced from both pulsar observations (Reynolds 1989, Gaensler et al. 2008) and from the rate of decrease in the H intensity with increasing Galactic latitude for the gas associated with the Perseus spiral arm (e.g., Haffner et al. 1999). The WIM accounts for 90% or more of the ionized hydrogen within the interstellar medium, and along lines of sight at high Galactic latitude (i.e., away from the Galactic midplane), the column density of the H⁺ is approximately 1/3 that of the neutral hydrogen (Reynolds 1991a).

Although originally detected by radio observations, subsequent developments in high-throughput Fabry-Perot spectroscopy and CCD imaging techniques have demonstrated that the primary source of information about the distribution, kinematics, and other physical properties of the WIM is through the detection and study of faint interstellar emission lines at optical wavelengths. For example, the distribution of the H⁺ is revealed by its interstellar H (6563) recombination line emission, which covers the sky. Several deep H surveys have given us our first detailed view of the distribution and kinematics of this gas. Through CCD imaging, Dennison et al. (1998) has provided partial coverage of the total H intensity in the northern sky, while Gaustad et al. (2001) covered the southern sky at arcminute resolution and sensitivities around 1 R (10⁶ / 4 photons cm^-2 s^-1 sr^-1; EM = 2.25 cm^-6 pc at 8000 K). The Wisconsin H-Alpha Mapper (WHAM) carried out a velocity resolved survey of the northern sky (dec. > 30°) at 12 km s^-1 spectral resolution, 1° spatial resolution, and ~ 0.1 R sensitivity (Haffner et al. 2003, Tufte 1997). The WHAM maps show WIM emission in virtually every beam, with faint loops, filaments, and blobs of emission superposed on a more diffuse background. Finkbeiner (2003) has combined these three surveys to form a composite all-sky view of the velocity-integrated H (Fig. 1).

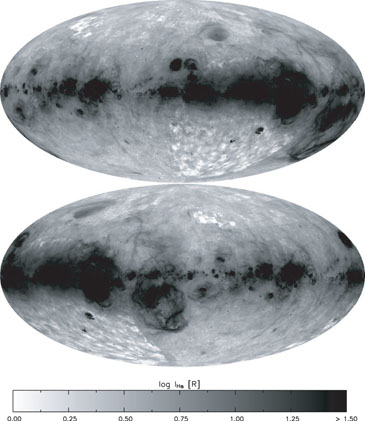Figure 1. Composite all-sky velocity-integrated H map. Data from VTSS, SHASSA, and the WHAM northern sky survey (WHAM-NSS) have been combined to produce these very deep (EM 1 cm-6 pc) emission maps. The two Aitoff-Hammer projections are centered at (top) = 0° and (bottom) = 180°. Areas covered by the imaging surveys have arc-minute resolution while those only surveyed by WHAM have one-degree resolution. Emission is predominantly from the Galaxy, although the imaging surveys can contain other bright, extended sources from the local universe (|vLSR| 500 km s-1; LMC, SMC, M31, etc.). Adopted from Finkbeiner (2003).

With these new maps and methods for detecting faint emission lines, we are now able to investigate the physical conditions of the WIM, its relationship to other components of the interstellar medium, and to sources of ionization and heating within the Galaxy. In particular, standard nebular line diagnostic techniques can now be employed to examine the physical conditions in the gas. In the low density (~ 10^-1 cm^-3) environment of the WIM, the collisional excitation of an ion to a metastable state 2-3 eV above ground by the thermal (~ 10⁴ K) electrons is followed by the decay back to the ground state via a "forbidden" optical transition. Specifically, the ion's excitation rate r_i n_i n_e T_e^-0.5 exp(-E / kT_e), where n_i and n_e are the volume densities of the ions and electrons, respectively, T_e is the electron temperature, and E is the energy of the metastable state above ground. Because thermal equilibrium between electrons and ions is very rapid, the temperature of the ions T_i = T_e (e.g., Spitzer 1978). Thus a variation in the photon emissivity of a forbidden line from one direction to the next traces variations in the temperature, density, and abundance of the ion. The effects of density variations can be eliminated by dividing the forbidden line intensity by the H-recombination line intensity, both of which are proportional to the product n_i n_e. From the intensities of lines from a number of different ions and atoms, it has been possible to study separately variations in the temperature and the ionization state within the emitting gas. For many years, these diagnostic techniques have been applied to a variety of astrophysical plasmas (see, e.g., Osterbrock 1989, Osterbrock and Ferland 2006, Dopita and Sutherland 2003, Ferland 2003, Davidson and Netzer 1979) for in depth discussions), but only more recently has it been possible to use them to study the much fainter WIM emission lines.

For example, in the WIM, the forbidden lines [S II] 6716 and [N II] 6584 are found to have intensities with respect to H that range from a few tenths to unity or higher, significantly larger than what is observed for the bright, classical emission nebulae (i.e., H II regions) immediately surrounding O stars. This implies that the physical conditions in the WIM differ significantly from conditions in classical H II regions. In addition, because their intensities are comparable to H, it has been possible to map these lines over large parts of the sky (e.g., Madsen et al. 2006). Other lines, such as [N II] 5755, He I 5876, [O III] 5007, and [O I] 6300, are much fainter and have been studied only in a few select directions. These observations have helped to characterize the ionization and temperature of the WIM as well as other extended ionized regions of the Galaxy. Results reveal that not only are the temperature and ionization conditions of the WIM significantly different from the conditions in classical O star H II regions, but that the conditions within the WIM itself vary considerably from one direction to the next and even along a single line of sight (Madsen et al. 2006).

2.2. Ionization state

The strength of the ionizing radiation field responsible for the WIM can be probed by measuring the H surface brightness of neutral hydrogen (H I) clouds and by measuring the hydrogen ionization fraction H⁺ / H within the WIM. Field (1975) pointed out that an H I cloud immersed in an ionizing radiation field will have a skin of H⁺ with an emission measure that is directly proportional to the incident photon flux. Using this fact, Reynolds et al. (1995) found that an interstellar Lyman continuum flux 4 J 2 × 10⁶ photons cm^-2 s^-1 could account for most of the WIM's ionization. This flux implies an ionizing photon density to electron density ratio (the ionization parameter) of 10^-4 to 10^-3, which is one to two orders of magnitude smaller than the ionization parameter in classical O star H II regions. However, values in this range still imply that the hydrogen is nearly fully ionized within the WIM. This is confirmed by more direct measurements of the hydrogen ionization fraction from the detection of neutral oxygen emission.

In theory, directly measuring the degree of H-ionization within warm, ionized gas is simply a matter of observing the [O I] 6300 emission line, which is produced by collisions of neutral oxygen with thermal electrons within the WIM. The first ionization potential of O is quite close to that of H (13.595 eV and 13.614 eV, respectively) and the large H⁺ + O⁰ 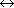H⁰ + O⁺ charge-exchange cross section keeps O⁺/O nearly equal to H⁺ / H. Electron energies in T_e ~ 10⁴ K gas are sufficient to excite the ~ 2 eV (³P-¹D) transition that results in the [O I] 6300 emission. Therefore, the intensity of this line relative to H is directly related to the amount of O⁰, and thus H⁰, relative to H⁺ in warm ionized gas (Reynolds et al. 1998). In practice, nature conspires to make this observation very difficult, because [O I] is also one of the brightest terrestrial emission lines in the night sky. Nevertheless, high-sensitivity, high-resolution spectroscopic measurements with WHAM have managed to resolve the Galactic emission from atmospheric emission to provide reliable measurements in a few select directions. These observations indicate that H⁺ / H > 90% for T > 8000 K (Reynolds et al. 1998, Hausen et al. 2002]).

The time scale for recombination at a typical WIM density of 0.1 cm^-3 is 1 Myr. This is shorter than the lifetimes of O stars, the presumed ionizing sources, which implies that the photoionization rate of the neutral hydrogen atoms within the WIM is roughly balanced by the rate of hydrogen recombination. In this case, the limit on H⁺ / H implies an ionizing flux > 10⁵ photons cm^-2 s^-1, consistent with the ionizing photon flux derived from the H surface brightness of H I clouds.

Regarding heavier ions, observations reveal that in the WIM ions are generally in lower states of ionization than in classical O star H II regions (e.g., Madsen et al. 2006). The reason is not yet fully understood, since Lyman continuum photons emitted by massive O stars are almost certainly the primary source of ionization for the WIM (see Section 3 and Section 4 below). The lower ionization state could be due to a softening of portions of the spectrum as the radiation travels from the O stars to the WIM. Photoionization models (Wood and Mathis 2004, Hoopes and Walterbos 2003) show that the spectral processing of the radiation can be complex, with the radiation between the H I and He I ionization edges hardening with distance from the source, while the spectrum at higher energies softens. Moreover, hot evolved low mass stars (white dwarfs) and interface radiation associated with the hot (10^5-6 K) gas add harder photons to the mix (Section 6). Independently of the spectrum, the low ionization state of the WIM also could be the result of its low ionization parameter (Mathis 1986).

Constraints on the fluxes of higher energy (i.e., helium-ionizing) photons are from observations of the He I recombination line at 5876 and the [O III] 5007 collisionally excited line. Both of these transitions are prominent in O star H II regions, where I(> 24 eV) is high enough (and is known to be high enough) to maintain He⁺ (24.6 eV) and O⁺⁺ (35.1 eV) at appreciable levels. Even qualitatively, from the first attempts to detect these lines in the WIM (Reynolds and Tufte 1995, Reynolds 1985a), it was clear that these ions were not as abundant in the WIM. More recent WHAM observations found (He I / H)_WIM ~ 0.5 × (He I / H)_{H II}, which when combined with the fact that H⁺ / H is near unity (see above), implies that He⁺ / He 60%. The [O III] / H results are more varied, although the ratios are typically less (~ 10%) those seen in H II regions (Madsen 2004, Madsen et al. 2006). The abundance of [O III] in other galaxies and in the interior regions of our Galaxy can be significantly higher than what is observed in the WIM near the sun (Rand 1997, Madsen and Reynolds 2005).

2.3. Temperature

The temperature of photoionized gas is set by a balance between heating and cooling. Heat is injected by thermalization of the excess kinetic energy of the electron during the photoionization-recombination process (see, e.g., Osterbrock 1989). Other potential sources of heat could also be important, particularly at the low densities characteristic of the WIM (see e.g., Reynolds and Cox 1992). Cooling occurs primarily from the collisional excitation and subsequent radiative decay of metastable states (i.e., forbidden lines) of the trace ions (see, e.g., Osterbrock 1989 for a detailed discussion). The detection of some of these "cooling lines" in combination with the H-recombination emission have been used to explore the temperature of the gas, as discussed in more detail below. The observations have established that 1) on average the WIM is about 2000 K warmer than the denser, classical H II regions and 2) there are significant variations in temperature within the WIM, most notably an increase in temperature with increasing distance away from the midplane, and more generally, with decreasing emission measure (or gas density). The reason for this temperature behavior of the WIM is not yet clear; it could indicate that photoionization is not the only important source of heat in the WIM (Reynolds et al. 1999) or that perhaps the spectrum of the ionizing radiation is modified as it propagates far from its source (see Section 5).

Although they vary in accuracy and difficulty, three tools are available to explore the temperature of the WIM through optical emission lines:

1. [N II] / H and [O II] / H trace variations in T_e: N⁺, O⁺, and H⁺ are the dominant states of ionization for these elements in the WIM. In addition, their emission lines have different dependences on temperature, so that changes in [N II] / H and [O II] / H closely track changes in T_e. Empirically, where I_H < 1 R, the brightnesses of the primary optical forbidden lines of [N II], [S II], and [O II] become comparable to H, making these lines easier to detect and thus attractive diagnostic tools for exploring variations in T_e. Calculating absolute temperatures is more uncertain due to necessary assumptions about the exact ionic fractions and elemental abundances.

2. [N II] 5755 / [N II] 6583 measures T_e directly: The ratio of the "auroral" (5755) emission line (resulting from excitations to a metastable state 4.0 eV above ground) to that of the much brighter "nebular" (6583) transition (1.9 eV above ground) allows a derivation of T_e with the fewest assumptions. Since this ratio involves the same ion, it is proportional to e^{(E / k T_e)}, where Δ E is the difference in the excitation energy of the two states. Near 8000 K, a 2000 K change in temperature produces about a factor of two change in the ratio. However, because I₅₇₅₅ / I₆₅₈₃ ~ 0.01, this observation is extremely difficult for the WIM, where I_H ~ 1 R.

3. Widths of resolved line profiles are proportional to T_i: Comparing the width of the H line to the width of an emission line from the heavier N⁺ or S⁺ ion can be used to separate the thermal from the nonthermal motions in the gas. However, very high signal-to-noise ratio line profile measurements are needed because the derived value of the ion temperature T_i is proportional to the difference of the squares of the line widths.

Results using these techniques in recent observations are summarized below.

2.3.1. [N II], [S II] and [O II] with respect to H

Two robust statements can be made about the line ratio observations:

1. [N II] / H, [S II] / H, and [O II] / H increase with decreasing I_H. In the Galaxy, this rise is most dramatic below I_H = 1 R. The clearest examples of this are the large increases in the forbidden line intensities relative to H with increasing distance from the midplane, both in our Galaxy (Haffner et al. 1999) and others (Rand 1998, Tüllmann et al. 2000).

2. Values for [S II] / H and [N II] / H vary greatly, but are strongly correlated, often with a nearly constant [S II] / [N II] ratio over large regions. For the Galaxy, the ratio of [S II] / [N II] does not vary by more than about a factor of two, except in the vicinity of a discrete ionizing source (e.g., an O star).

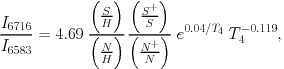(1)

which is only a very weak function of T₄ ( T_e/10⁴ K). From T₄ = 0.5 to 1.0 with all else constant, [S II] / [N II] decreases only about 11%. This relationship also indicates that the relatively small but real variations of [S II] / [N II] that are observed in the WIM are tracing variations of S⁺ / N⁺. Combined with the very different energies required for S⁺ S⁺⁺ (23.3 eV) and N⁺ N⁺⁺ (29.6 eV), we conclude that S⁺ / S, and especially N⁺ / N, vary little in the WIM and that the smaller (factor of two) variations in [S II] / [N II] are due primarily to variations in S⁺ / S. This is supported by photoionization models (e.g., Sembach et al. 2000), which have shown that N⁺ / N 0.8 over a wide range of input spectra and ionization parameters.

On the other hand, the strong temperature dependence of the forbidden line intensities relative to H is illustrated by the relationship for the [N II] / H

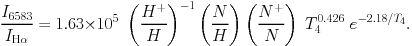(2)

Because N⁺ / N and H⁺ / H vary little within the WIM, variations in [N II] / H essentially trace variations in T_e. Similar relationships can be written for [O II], [S II], and for other collisionally excited lines (see Otte et al. 2001).

Using Eq. 1 and 2, we can construct diagnostic diagrams as presented by Haffner et al. (1999) and Madsen et al. (2006) to estimate both T_e and S⁺ / S from observations of [N II] / H and [S II] / H, as shown in Fig. 2 (adapted from Madsen 2004). With sufficient velocity resolution it has even been possible to study variations in these parameters between different radial velocity components along the same line of sight. These results reveal that within the WIM there are variations in temperatures ranging between about 7000 K and 10000 K and variations in S⁺/S between 0.3 to 0.7. For comparison, the bright classical H II regions all cluster near the lower left corner of the plot, [S II] / H 0.1 and [N II] / H 0.25, where T_e = 6000-7000 K and S⁺ / S 0.25.

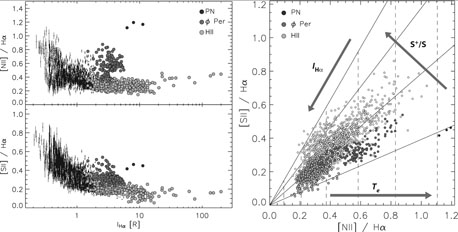Figure 2. Diagnostic line ratio diagrams. A large portion of the Galaxy in the direction of the Perseus arm ( = 130° to 160° and b = -30° to +30°, approximately) has been surveyed in H, [S II], and [N II] with WHAM. These panels show (left) the relationship between the ratios versus the intensity of H as well as (right) the relationship between the two ratios for the "local" gas component (|vLSR| < 15 km s-1). A few specific spatial regions are highlighted with grayscale fill to show effects of local ionizing sources: the planetary nebula (PN) S216, the H II region surrounding the B0.5+sdO system ϕ Per, and regions near O-star H II regions. Other data points sample the WIM. In the diagram on the right, the vertical dashed lines represent Te, 5000 K, 6000 K, 7000 K, 8000 K, 9000 K, and 10000 K, left to right. The slanted solid lines represent S+/S, 0.25, 0.50, 0.75, and 1.00, lowest to highest slope. These WIM data reveal significant variations in Te and S+/S from one line of sight to the next. In contrast, classical H II regions all cluster in the lower left corner of this diagram near [N II] / H 0.25, [S II] / H 0.1. From Madsen(2004).

[O II] at 3727 has a larger excitation energy than [N II], making it even more sensitive to variations in T_e. Although inaccessible with WHAM, several extragalactic studies (Otte et al. 2002, Otte et al. 2001, Tüllmann and Dettmar 2000) have traced this line, and new instrumentation is starting to allow studies of [O II] from the WIM (Mierkiewicz et al. 2006) of the Milky Way. The [O II] observations confirm that the line ratio variations are dominated by variations in T_e.

2.3.2. [N II] 5755 / [N II] 6583

One of the most direct ways of measuring T_e in ionized gas is to observe the ratio of two emission lines from the same ion but with very different excitation energies above ground. The I₄₃₆₃ / I₅₀₀₇ ratio of [O III] in bright H II regions is perhaps the most famous of these pairs. In the WIM, because the [O III] / H ratios are typically no more than 10% of that in H II regions, the isoelectronically similar [N II] line ratio, I₅₇₅₅ / I₆₅₈₃, has been used instead.

By detecting this extremely weak line, Reynolds et al. (2001b) and Madsen (2004) confirmed in select directions that T_e in the WIM is indeed higher by about 2000 K than in the bright H II regions. However, the details of the results reveal a more complicated temperature structure-perhaps not surprisingly. Although current measurements of the 5755 line still have large uncertainties, Fig. 3 indicates that T_e as inferred by the ratio of the [N II] lines is systematically higher than that inferred by [N II] / H in the same directions. This could be explained by temperature variations along the line of sight, since the 5755 line (excitation energy 4 eV) would be produced preferentially in regions with higher T_e compared to the red line (2 eV).

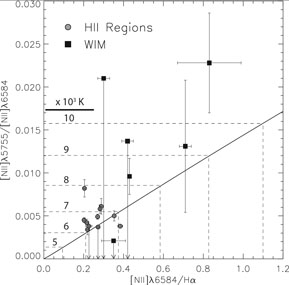Figure 3. Elevated temperature in the WIM. Select directions toward () brighter diffuse ionized regions show elevated line ratios in both [N II] / H and [N II] 5755 / 6584 compared to () H II regions. Dashed lines mark select temperatures derived from each line ratio while the diagonal line traces "unity" in this derived temperature space. WIM directions have higher derived temperatures using either line ratio, but are also systematically above the line of "unity", suggesting that measurable temperature inhomogeneities exist along these lines of sight. From Madsen(2004).

2.3.3  Line widths

If the intrinsic widths of emission lines can be measured accurately in ions having significantly different masses, then one can decompose the thermal motion (i.e., T_i) and non-thermal motion contributing to their widths. H and S are particularly good to use because they differ in mass by a factor of 32, resulting in a measurable difference in their widths. This method has been used with some success in both the WIM (Reynolds 1985b) and H II regions (Reynolds 1988).

The potential power of this technique is illustrated in Fig. 4, which shows line width data for the large, high Galactic latitude H II region surrounding the O star (O9.5V) Oph. The H from this region spans an order of magnitude in intensity and at the fainter end becomes comparable to WIM emission at low Galactic latitudes (~ 10 R). The Oph H II region is particularly good for line width studies because each emission line profile is very well described by a single Gaussian component. Baker et al. (2004) measured the widths of the H, [S II], and [N II] emission lines from this region and derived accurate values for the temperature T_i and the mode of the nonthermal speeds v_NT as shown in Fig. 4. The large ranges in these parameters appears to be real, with a noticeable gradient of increasing T_i (from 6000 to 8000 K) and decreasing v_NT (from 8 to 4 km s^-1) from the center to edge of the H II region. The former is ascribed to the hardening of the radiation field with increasing distance from the source (also Wood et al. 2005, Section 5 below), while the latter could be explained by a slow (2 km s^-1) expansion of the H II region. A future goal is to extend this method to the fainter and more kinematically complex WIM.

Figure 4. Temperature Ti and the mode vNT (most probable value) of the non-thermal speed distribution of the diffuse H II region surrounding Oph. The primary axes show the measured widths and errors of H and [S II] from 126 one-degree pointings obtained by WHAM within a 12-degree diameter region around Oph. A grid of temperatures and non-thermal velocities has been superimposed to show the distribution of Ti and vNT within the H II region. The apparent scatter in these values is spatially correlated (see text). The line at the upper-left is the line of equal widths.

In summary, the evidence is now overwhelming from a variety of methods that in the WIM the temperature is elevated compared to the bright, classical H II regions. In addition, the large variations in optical forbidden line strength relative to H within the WIM is dominated by changes in temperature rather than changes in ionic fractions or elemental abundances. When this is combined with the well-established result that the forbidden line ratios relative to H increase with decreasing H intensity (statement (a), above), we are led to the conclusion that the temperature increases with decreasing emission measure (Haffner et al. 1999) and thus decreasing gas density. These temperature variations do not appear to be explained solely by photoionization heating of the gas (Wood and Mathis 2004, Reynolds et al. 1999), suggesting additional heating sources for the WIM (Weingartner and Draine 2001, Minter and Spangler 1997, Reynolds and Cox 1992) that begin to dominate over photoionization heating at low densities (~ 10^-1 cm^-3).

2.4. Warm ionized and neutral gas

The fact that hydrogen is nearly fully ionized within the H emitting gas (Section 2.2) implies that H⁺ and H⁰ are primarily confined to separate regions. With the advent of velocity resolved H surveys (i.e., WHAM), it is now possible to begin to explore the relationship between the diffuse ionized gas and neutral gas in the interstellar medium. Is the WIM the ionized portion of a low density "intercloud medium" (Miller and Cox 1993) or is it mostly confined to the surfaces of neutral clouds, the transition region between cooler gas and a much hotter "coronal" temperature medium (McKee and Ostriker 1977)? Do the ionized and neutral phases cycle from one to the other? Cox and Helenius (2003) and Lockman (2004), for example, have suggested that portions of the ionized medium may condense into neutral clouds. However, to date there have been no observational studies of the H⁺ - H⁰ connection. In a general qualitative sense, a comparison of the optical line profiles with the radio 21 cm (H I) profiles (e.g., Hartmann and Burton 1997), indicates that at high latitudes the ionized gas tends to be correlated in space and velocity with the so-called warm neutral medium (WNM), the wide-spread, T ~ 10³ K phase of the H I generally associated with broad 21 cm profiles. There is very little correspondence between the H and the narrow-line 21 cm emission components associated with the colder (T ~ 10² K), denser H I clouds. In regions of the sky that contain anomalous velocity structures, specifically, the intermediate and high velocity clouds that are not co-rotating with the Galactic disk, the correlation is quite strong (Haffner et al. 2001, Tufte et al. 1998). The optical and radio emission components are centered at nearly the same velocities (within roughly 5 km s^-1) and have comparable velocity extents in cases of complicated, blended profiles. Few regions seem to contain only a WNM or only a WIM component. This relationship has been hinted at through various detailed absorption line and emission line studies over the last decade (Spitzer and Fitzpatrick 1993, Howk et al. 2003, Reynolds et al. 1995), which together with observations of the [O I] 6300 / H line intensity ratio (Section 2.3 above) suggest that a significant amount of the H⁺ is associated with nearly fully ionized regions in contact with (or at least adjacent to) regions of warm primarily neutral hydrogen. Hopefully a systematic examination of the kinematic and spatial correlation between these ionized and neutral phases of the medium will be carried out soon.

Although there is a close correspondence on the sky and in velocity between the warm neutral and ionized emission lines, their intensities do not appear to be correlated. This has been examined in detail only toward two intermediate velocity H I clouds, Complexes L and K (Haffner 2005, Haffner et al. 2001). In both cases, the column density of the neutral hydrogen N_{H I} and the H intensity, I_H, are uncorrelated. Whether this holds for more local gas in the Galactic disk still needs to be fully explored. A straightforward explanation for this lack of correlation is the fact that the intensity of the H is determined solely by the flux of ionizing radiation incident on the warm H I cloud (Reynolds et al. 1995), which of course, is independent of the cloud's column density because the H I clouds are optically thick to the Lyman continuum photons.

2.5. The role of superbubbles

One of the basic questions concerning the nature of the WIM is how ionizing photons from the O stars can travel hundreds of parsecs through the disk and into the halo. A fractal morphology of the interstellar medium is one possibility (see Section 5). Another is the existence of enormous, H I-free bubbles surrounding some of the O stars, which allow the Lyman continuum photons to travel through the cavity to ionize its distant walls (e.g., Reynolds and Ogden 1979, Norman and Ikeuchi 1989, McClure-Griffiths et al. 2006 , Pidopryhora et al. 2007). A WHAM study of one of these bubbles, the Perseus superbubble (Madsen et al. 2006, Reynolds et al. 2001a), has shown that a luminous O-star cluster near the midplane can indeed produce wide-spread, nearly WIM-like ionization conditions out to distances of 1000 pc or more from the ionizing stars. However, the [N II] / H and [S II] / H ratios of the superbubble wall are not quite as large as the ratios observed in the surrounding WIM, suggesting that bubble size, gas density within the shell, supplemental heating, and/or the flux and spectrum of the radiation escaping the O-star cluster may also be important in setting the conditions of the ionized gas.