2. SELF-GRAVITATING SYSTEMS EVOLVE BY SPREADING

This is the most fundamental section of this review. I want to give you a heuristic, intuitive understanding of why secular evolution happens in disk galaxies. And I want to show you how the evolution of essentially all self-gravitating systems is fundamentally similar. The theme of this Winter School is the disk-galaxy version of that more general evolution.

I made this point in Kormendy & Fisher (2008) and in Kormendy (2008a). However, it is important enough – especially at a school – that I repeat it here in detail. The following is a slightly expanded and paraphrased version of the discussion in Kormendy (2008a).

The general principle that drives the evolution of self-gravitating systems is this: it is energetically favorable to spread. That is, as energy or angular momentum is transported outward, the inner parts shrink and grow denser, while the outer parts expand, grow more diffuse, and, in some cases, escape the system. How to see this depends on whether the system is dominated by rotation or by random motions.

2.1. If dynamical support is by random motions

For systems that are dominated by velocity dispersion, the argument is given by Lynden-Bell & Wood (1968) and by Binney & Tremaine (1987). The essential point is that the specific heat of a self-gravitating system is negative. Consider an equilibrium system of N particles of mass m, radius r and three-dimensional velocity dispersion v. The virial theorem tells us that 2 KE + PE = 0, where the kinetic energy is KE = Nmv²/2 and the potential energy is PE = -G(Nm)² / r. The total energy E ≡ KE + PE = -KE is negative. This is what it means to be a bound system. But the temperature of the system is measured by v²: mv²/2 = 3kT / 2. So the specific heat C ≡ dE / dT ∝ d(-Nmv²/2) / d(v²) is also negative. In the above, G is the gravitational constant and k is Boltzmann's constant.

The system is supported by heat, so evolution is by heat transport. If the center of the system gets hotter than the periphery, then heat tends to flow outward. The inner parts shrink and get still hotter. This promotes further heat flow. The outer parts receive heat; they expand and cool. Whether the system evolves on an interesting timescale depends on whether there is an efficient heat-transport mechanism. For example, many globular clusters evolve quickly by two-body relaxation and undergo core collapse. Giant elliptical galaxies – which otherwise would evolve similarly – cannot do so because their relaxation times are much longer than the age of the Universe.

2.2. If dynamical support is by rotation

Tremaine (1989) provides a transparent summary of an argument due to Lynden-Bell & Kalnajs (1972) and to Lynden-Bell & Pringle (1974). A disk is supported by rotation, so evolution is by angular momentum transport. The "goal" is to minimize the total energy at fixed total angular momentum. A rotationally supported ring at radius r in a fixed potential Φ(r) has specific energy E(r) and specific angular momentum L(r) given by

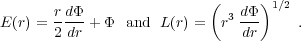(1)

Then dE/dL = Ω(r), where Ω = (r^-1 dΦ / dr)^1/2 is the angular speed of rotation. Disks spread when a unit mass at radius r₂ moves outward by gaining angular momentum dL from a unit mass at radius r₁ < r₂. This is energetically favorable: the change in energy,

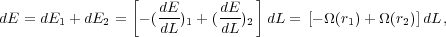(2)

is negative because Ω(r) usually decreases outward. "Thus disk spreading leads to a lower energy state. In general, disk spreading, outward angular momentum flow, and energy dissipation accompany one another in astrophysical disks" (Tremaine 1989).

2.3. Spreading in various kinds of self-gravitating systems

The consequences are very general. All of the evolution summarized in Fig. 2 happens because of the above physics.

Figure 2. Powerpoint slide that emphasizes the underlying similarity in evolutionary processes that shape various kinds of self-gravitating systems. The secular evolution of galaxy disks (top row) is the subject of my lectures.

Protostars are spherical systems coupled to circumstellar disks by magnetic fields that wind up because of differential rotation. This drives jets that look one-dimensional but that really are three-dimensional; they carry away angular momentum and allow the inner circumstellar disk to shrink and accrete onto the star (Shu et al. 1994, 1995).

An accretion disk around a black hole is supported by rotation, so it evolves by angular momentum transport. The evolution happens because of magnetic coupling between various parts of the accretion disk. The details are complicated, but the net effect is that some material flows outward as part of a jet and other material is accreted onto the black hole. Note again that pictures of this process – whether observations of radio jets or artists' conceptions of the accretion process – almost always show narrow jets. But, as in the case of protostars, outward angular momentum transfer must be involved in order for some of the material to accrete onto the black hole.

Galactic disks are supported by rotation. They spread in two dimensions by outward angular momentum transport. Efficient engines are provided by bars and by oval disks. Like all of the above, the evolution is secular – slow compared to the collapse time or crossing time of the disk. The growth of a pseudobulge in a galactic disk is as natural as the growth of a star in a protostellar disk and as the growth of a black hole in a black hole accretion disk. Only the processes that transport angular momentum are different.

This secular evolution is the subject of my paper and this Winter School.

2.4. What kinds of galaxy disks evolve secularly?

For secular evolution to happen, a galaxy needs two things. It needs a driving mechanism such as a bar, a globally oval disk (Section 3.3), or global spiral structure. And disk spreading must be energetically favorable. Equation (2) tells us that it is more energetically favorable to transport angular momentum outward the more the angular rotation velocity Ω(r) decreases outward. This lets us divide galaxies into three types, as follows.

Galaxies that lack driving agents should not show strong secular evolution. Examples are unbarred galaxies with classical bulges and weak or no global spiral structure (e. g., M 31, NGC 2841 and NGC 4594, the Sombrero Galaxy). We will see that these objects generally do not show centrally concentrated molecular gas and star formation. We take this as an sign that secular evolution largely is not happening.

For galaxies with engines, Fig. 3 shows how the tendency to evolve depends on the mass distribution as revealed by the rotation curve V(r). Where V(r) increases proportional to r (or even rather more slowly), the angular rotation velocity Ω(r) is constant (or very slowly decreasing outward). This means that it is not energetically favorable to evolve. This is the situation in an Scd galaxy like M 33, where we find no pseudobulge.

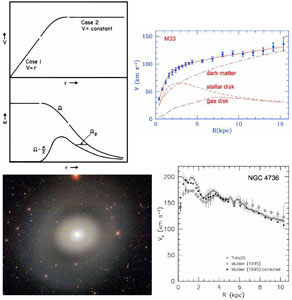Figure 3. Typical examples of spiral galaxies that do (NGC 4736, bottom) and do not (M 33, top) have mass distributions that are conducive to secular evolution. The top-left plots (Kormendy & Norman 1979) show a generic rotation curve V(r) and associated angular velocity curves Ω(r) ≡ V(r) / r and Ω -κ / 2, where κ is the epicyclic frequency. Where V ∝ r, Ω = constant and secular evolution is not energetically favorable. Even where V(r) is turning downward from V ∝ r toward V = constant, Ω decreases outward so slowly that secular evolution is disfavored. This is the situation throughout a galaxy like M 33 (top-right rotation curve and rotation curve decomposition, from Corbelli & Salucci 2000). M 33 has neither a classical bulge nor a significant pseudobulge. In contrast, NGC 4736 (image at bottom-left, from http://www.wikisky.org) has a rotation curve that decreases outward with radius, as derived by de Blok et al. (2008; bottom-right panel here). Disk spreading is energetically very favorable. Moreover, NGC 4736 is a prototypical strongly oval galaxy, so it has an engine for secular evolution. Not surprisingly, it is our best "poster child" for secular evolution – an unbarred galaxy with a pseudobulge identified by five classification criteria (Section 5.3).

The Corbelli & Salucci (2000) decomposition of the M 33 rotation curve into contributions due to the stellar disk, the gas disk and the dark matter halo reveals an additional reason why secular evolution is disfavored. The contribution of the dark matter to V(r) is everywhere comparable to or larger than that of the visible matter. But dark halos are dynamically much hotter than disks. They do not participate in disk dynamics. The observation that the self-gravity of the disk is "diluted" by the gravity of the much stiffer halo is a further sign that secular evolution is disfavored. Kormendy & McClure (1993) show that M 33 contains a nuclear star cluster (like a large globular cluster) but no significant evidence for a pseudobulge.

In contrast, if a galaxy has a flat rotation curve, then Ω ∝ 1/r and secular evolution is energetically favorable (top-left panels of Fig. 3). Even more extreme are galaxies in which the rotation curve decreases outward. De Blok et al. (2008) conclude that the rotation curve of NGC 4736 decreases outward (Fig. 3, bottom-right). ¹ Under these circumstances, secular evolution should be especially important. In fact, NGC 4736 turns out to be our best "poster child" for secular evolution in an unbarred galaxy (see also Fig. 6, Section 3, Fig. 8, Fig. 28, Fig. 31, Fig. 35, Fig. 38, Table 3).

It will turn out that angular momentum redistribution and therefore radial mass transport happens mostly to gas. The need for gas disfavors early-type galaxies and favors late-type galaxies.

Putting all this together, we can already foresee what the observational review in the rest of this paper will reveal: Secular evolution in galaxy disks is, in the current Universe, happening mostly in intermediate-late-type (e. g., Sbc) galaxies. These are the galaxies in which pseudobulges turn out to be most prominent. Secular evolution is too slow to be important in the latest-type galaxies, because the mass distribution is too "fluffy", and so it is not energetically favorable to transport angular momentum outward. And secular processes no longer transport much gas in S0 and Sa galaxies, because they no longer contain much gas. Nevertheless, (1) purely stellar secular processes are expected to happen in these galaxies, and (2) secular evolution is believed to have been important in the past, because many S0 galaxies are observed to contain disky pseudobulges.

I turn next to a discussion of our motivation and where it will lead us.

¹ This result depends on the assumption that the gas is on circular orbits everywhere in the galaxy and that asymmetries in the velocity field and in the galaxy image (Fig. 3, bottom-left) are due to warps. These assumptions are not valid. NGC 4736 has an oval disk (Bosma et al. 1977; Kormendy 1982b, 1993b; Kormendy & Kennicutt 2004; Fig. 8 here). A suitable analysis of the velocity field based on plausible axial ratios for the inner disk and outer ring has not been made. However, it is likely that the true rotation curve decreases outward more slowly than Fig. 3 suggests. Nevertheless, disk secular evolution is more energetically favorable in NGC 4736 than it is in most galaxies. Back.