Annu. Rev. Astron. Astrophys. 2002. 40:487-537 Copyright © 2002 by Annual Reviews. All rights reserved

4. SIGNATURES OF GALAXY FORMATION

Our framework is that the Galaxy formed through hierarchical aggregation. We identify three major epochs in which information about the proto-hierarchy is lost:

1. the dark matter virializes – this could be a time of intense star formation but need not be, as evidenced by the existence of very thin pure disk galaxies;
2. the baryons dissipate to form the disk and bulge;
3. an ongoing epoch of formation of objects within the disk and accretion of objects from the environment of the galaxy, both leaving some long-lived relic.

We classify signatures relative to these three epochs. The role of the environment is presently difficult to categorize in this way. Environmental influences must be operating across all of our signature classes.

4.1. Zero Order Signatures – Information Preserved Since Dark Matter Virialized

4.1.1. Introduction

During the virialization phase, a lot of information about the local hierarchy is lost: This era is dominated by merging and violent relaxation. The total dark and baryon mass are probably roughly conserved, as is the angular momentum of the region of the hierarchy that went into the halo. The typical density of the environment is also roughly conserved: Although the structure has evolved through merging and relaxation, a low density environment remains a low density environment (see White 1996 for an overview).

4.1.2. Signatures of the environment

The local density of galaxies (and particularly the number of small satellite systems present at this epoch) affects the incidence of later interactions. For the Local Group, the satellite numbers appear to be lower than expected from CDM (Moore et al. 1999, Klypin et al. 1999). However there is plenty of evidence for past and ongoing accretion of small objects by the Milky Way and M31 (Ibata et al. 1995, 2001b).

The thin disk component of disk galaxies settles dissipatively in the potential of the virialized dark halo (e.g., Fall & Efstathiou 1980). The present morphology of the thin disk depends on the numbers of small galaxies available to be accreted: A very thin disk is an indication of few accretion events (dark or luminous) after the epoch of disk dissipation and star formation (e.g., Freeman 1987, Quinn et al. 1993, Walker et al. 1996). The formation of the thick disk is believed to be associated with a discrete event that occurred very soon after the disk began to settle, at a time when about 10% of the stars of the disk had already formed. In a low density environment, without such events, thick disk formation may not occur. Since the time of thick disk formation, the disk of the Galaxy appears to have been relatively undisturbed by accretion events. This is consistent with the observation that less than 10% of the metal-poor halo comes from recent accretion of star forming satellites (Unavane et al. 1996).

The existence and structure of the metal-poor stellar halo of the Galaxy may depend on accretion of small objects. This accretion probably took place after the gaseous disk had more or less settled – the disk acts as a resonator for the orbit decay of the small objects. So again the environment of our proto-galaxy may have a strong signature in the very existence of the stellar halo, and certainly in its observed substructure. We would not expect to find a stellar halo encompassing pure disk galaxies, consistent with the limited evidence now available (Freeman et al. 1983, Schommer et al. 1992).

4.1.3. Signatures of global quantities

During the process of galaxy formation, some baryons are lost to ram pressure stripping and galactic winds. Most of the remaining baryons become the luminous components of the galaxy. The total angular momentum J of the dark halo may contribute to its shape, which in turn may affect the structure of the disks. For example, warps may be associated with misalignment of the angular momentum of the dark and baryonic components. The dark halo may have a rotating triaxial figure; the effect of a rotating triaxial dark halo on the self-gravitating disk has not yet been seriously investigated (see Bureau et al. 1999).

The binding energy E at the epoch of halo virialization affects the depth of the potential well and hence the characteristic velocities in the galaxy. It also affects the parameter λ = J|E|^1/2 G⁻¹ M^−5/2, where M is the total mass: λ, which is critical for determining the gross nature of the galactic disk as a high or low surface brightness system (e.g., Dalcanton et al. 1997).

The relation between the specific angular momentum J / M and the total mass M (Fall 1983) of disk galaxies is well reproduced by simulations (Zurek et al. 1988). Until recently, ellipticals and disk galaxies appeared to be segregated in the Fall diagram: From the slow rotation of their inner regions, estimates of the J / M ratios for ellipticals were about 1 dex below those for the spirals. More recent work (e.g., Arnaboldi et al. 1994) shows that much of the angular momentum in ellipticals appears to reside in their outer regions, so ellipticals and spirals do have similar locations in the Fall diagram. Internal redistribution of angular momentum has clearly occurred in the ellipticals (Quinn & Zurek 1988).

The remarkable Tully-Fisher law (1977) is a correlation between the HI line-width and the optical luminosity of disk galaxies. It appears to relate the depth of the potential well and the baryonic mass (McGaugh et al. 2000). Both of these quantities are probably roughly conserved after the halo virializes, so the Tully-Fisher law should be regarded as a zero-order signature of galaxy formation. The likely connecting links between the (dark) potential well and the baryonic mass are (a) a similar baryon/dark matter ratio from galaxy to galaxy, and (b) an observed Faber-Jackson law for the dark halos, of the form M ∝ σ⁴: i.e., surface density independent of mass for the dark halos (J. Kormendy & K.C. Freeman, in preparation).

4.1.4. Signatures of the internal distribution of specific angular momentum

The internal distribution of specific angular momentum (h) of the baryons (i.e., the mass with specific angular momentum < h) largely determines the shape of the surface brightness distribution of the disk rotating in the potential well of the dark matter. Together with (h) the total angular momentum and mass of the baryons determine the scale length and scale surface density of the disk. Therefore the distribution of total angular momentum and mass for protodisk galaxies determines the observed distribution of the scale length and scale surface density for disk galaxies (Freeman 1970, de Jong & Lacey 2000).

Many studies have assumed that (h) is conserved through the galaxy formation process, most notably Fall & Efstathiou (1980). It is not yet clear if this assumption is correct. Conservation of the internal distribution of specific angular momentum (h) is a much stronger requirement than the conservation of the total specific angular momentum J / M. Many processes can cause the internal angular momentum to be redistributed, while leaving the J / M ratio unchanged. Examples include the effects of bars, spiral structure (Lynden-Bell & Kalnajs 1972) and internal viscosity (Lin & Pringle 1987).

The maximum specific angular momentum h_max of the baryons may be associated with the truncation of the optical disk observed at about four scale lengths (de Grijs et al. 2001, Pohlen et al. 2000). This needs more investigation. The truncation of disks could be an important signature of the angular momentum properties of the early protocloud, but it may have more to do with the critical density for star formation or the dynamical evolution of the disk. Similarly, in galaxies with very extended HI, the edge of the HI distribution may give some measure of h_max in the protocloud. On the other hand, it may be that the outer HI was accreted subsequent to the formation of the stellar disk (van der Kruit 2001), or that the HI edge may just represent the transition to an ionized disk (Maloney 1993).

This last item emphasizes the importance of understanding what is going on in the outer disk. The outer disk offers some potentially important diagnostics of the properties of the protogalaxy. At present there are too many uncertainties about the significance of (a) the various cutoffs in the light and HI distributions, (b) the age gradient seen by Bell & de Jong (2000) from integrated light of disks but not by Friel (1995) for open clusters in the disk of the Galaxy, and (c) the outermost disk being maybe younger but not “zero age,” which means that there is no real evidence that the disk is continuing to grow radially. It is possible that the edge of the disk has something to do with angular momentum of baryons in the protocloud or with disk formation process, so it may be a useful zero-order or first-order signature.

4.1.5. Signatures of the CDM hierarchy

CDM predicts a high level of substructure that is in apparent conflict with observation. Within galaxies, the early N-body simulations appeared to show that substructure with characteristic velocities in the range 10 < V_c < 30 km s^-1 would be destroyed by merging and virialization of low mass structures (Peebles 1970, White 1976, White & Rees 1978). It turned out that the lack of substructure was an artefact of the inadequate spatial and mass resolution (Moore et al. 1996). Current simulations reveal 500 or more low mass structures within 300 kpc of an L_* galaxy's sphere of influence (Moore et al. 1999, Klypin et al. 1999). This is an order of magnitude larger than the number of low mass satellites in the Local Group. Mateo (1998) catalogues about 40 such objects and suggests that, at most, we are missing a further 15−20 satellites at low galactic latitude. Kauffmann et al. (1993) were the first to point out the satellite problem and suggested that the efficiency of dynamical friction might be higher than usually quoted. However, without recourse to fine tuning, this would remove essentially all of the observed satellites in the Local Group today.

Since the emergence of the CDM paradigm, an inevitable question is whether a basic building block can be recognized in the near field. Moore et al. emphasize the self-similar nature of CDM sub-clustering and point to the evidence provided by the mass spectrum of objects in rich clusters, independent of the N-body simulations. The lure of finding a primordial building block in the near field has prompted a number of tests. If the dark mini-halos comprise discrete sources, it should be possible to detect microlensing towards a background galaxy (see “The Dark Halo” above).

The satellite problem appears to be a fundamental prediction of CDM in the nonlinear regime. Alternative cosmologies have been suggested involving the reduction of small-scale power in the initial mass power spectrum (Kamionkowski & Liddle 2000), warm dark matter (Hogan & Dalcanton 2001, White & Croft 2000, Colin et al. 2000), or strongly self-interacting dark matter (Spergel & Steinhardt 2000). Several authors have pointed out that some of the direct dark-matter detection experiments are sensitive to the details of the dark matter in the solar neighborhood. Helmi et al. (2001) estimate that there may be several hundred kinematically cold dark streams passing through the solar neighborhood.

If CDM is correct in detail, then we have simply failed to detect or to recognize the many hundreds of missing objects throughout the Local Group. For example, the satellites may be dark simply because baryons were removed long ago through supernova-driven winds (Dekel & Silk 1986, Mac Low & Ferrara 1999). In support of this idea, X-ray halos of groups and clusters are almost always substantially enriched in metals ([Fe/H] ≥ -0.5; Renzini 2000, Mushotzky 1999). In fact, we note that up to 70% of the mass fraction in metals is likely to reside in the hot intracluster and intragroup medium (Renzini 2000). Another explanation may be that the absence of baryons in hundreds of dark satellites was set in place long ago during the reionization epoch. Many authors note that the accretion of gas on to low-mass halos and subsequent star formation is heavily suppressed in the presence of a strong photoionizing background (Ikeuchi 1986, Rees 1986, Babul & Rees 1992, Bullock et al. 2000). This effect appears to have a cut-off at low galactic mass at a characteristic circular velocity close to 30 km s^-1 (Thoul & Weinberg 1996, Quinn et al. 1996), such that the small number of visible Local Group dwarfs are those that exceed this cutoff or acquired most of their neutral hydrogen before the reionization epoch.

Blitz et al. (1999) suggested that the high-velocity HI gas cloud (HVC) population is associated with dark mini-halos on megaparsec scales within the Local Group. This model was refined by Braun & Burton (1999) to include only the compact HVCs. The HVCs have long been the subject of wide-ranging speculation. Oort (1966) realized that distances derived from the virial theorem and the HI flux would place many clouds at Mpc distances if they are self-gravitating. If the clouds lie at about a Mpc and are associated with dark matter clumps, then they could represent the primordial building blocks. However, Hα distances (Bland-Hawthorn et al. 1998) suggest that most HVCs lie within 50 kpc and are unlikely to be associated with dark matter halos (Bland-Hawthorn & Maloney 2001, Weiner et al. 2001). We note that several teams have searched for but failed to detect a faint stellar population in HVCs.

Moore et al. (1999; see also Bland-Hawthorn & Freeman 2000) suggested that ultrathin disks in spirals are a challenge to the CDM picture in that disks are easily heated by orbiting masses. However, Font et al. (2001) found that in their CDM simulations, very few of the CDM sub-halos come close to the optical disk.

At present there are real problems in reconciling the predictions of CDM simulations with observations on scales of the Local Group.

4.2. First Order Signatures – Information Preserved Since the Main Epoch of Baryon Dissipation

4.2.1. The structure of the disk

At what stage in the evolution of the disk are its global properties defined? In part, we have already discussed this question in “Signatures of the Internal Distribution of Specific Angular Momentum” above. The answer depends on how the internal angular momentum distribution (h) has evolved as the disk dissipated and various nonaxisymmetric features like bars and spiral structure came and went. Viscous processes associated with star formation, as suggested by Lin & Pringle (1987), may also contribute to the evolution of the (h) distribution.

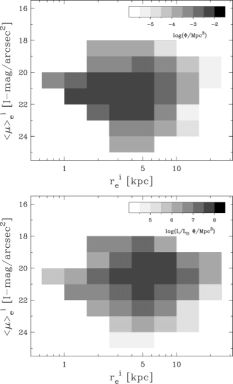
The global structure of disks is defined by the central surface brightnes I_o and the radial scalelength h of the disk. de Jong & Lacey (2000) evaluated the present distribution of galaxies in the (I_o, h) plane (Figure 4). If (h) has indeed remained roughly constant, as is often assumed for discussions of disk formation (e.g., Fall & Efstathiou 1980, Fall 1983), then the global parameters of the disk – the scale length, central surface brightness and the Tully-Fisher relation – are relics of the main epoch of baryon dissipation.

Figure 4. The density distribution of Sa to Sm galaxies over effective radius re and effective surface brightness µe. The top panel shows the raw (unweighted) distribution and the bottom panel shows the luminosity weighted distribution (de Jong & Lacey 2000).

4.2.2. Can disks preserve fossil information?

Here, we consider radial and vertical fossil gradients in the disk, in particular of abundance and age. Our expectation is that much of the information will be diluted through the dynamical evolution and radial mixing of the disk.

For spirals, different mechanisms may be at work to establish gradients (Molla et al. 1996): (a) a radial variation of the yield due either to the stellar metal production or to the initial mass function, (b) a radial variation of the timescale for star formation, (c) a radial variation for the timescale of infall of gas from outside the disk. Once gradients are established, these can be amplified or washed out by radial mixing (Edmunds 1990, Goetz & Koeppen 1992).

Most stars are born in large clusters numbering hundreds or even thousands of stars. Some clusters stay together for billions of years, whereas others become unbound shortly after the initial starburst, depending on the star formation efficiency. When a cloud disperses, each star suffers a random kick superimposed on the cloud's mean motion. Thereafter, stars are scattered by transient spiral arm perturbations and star-cloud encounters.

These perturbations allow the star to migrate in integral space. During interaction with a single spiral event of pattern speed Ω_p, a star's energy and angular momentum change while it conserves its Jacobi integral: In the (E, J) plane, stars move along lines of constant I_J = E - Ω_p J. The star undertakes a random walk in the (E, J) plane, perturbed by a series of spiral arm events (Sellwood 1999, Dehnen 2000). N-body models of disk evolution indicate that radial mixing is strong (Sellwood 2001, Lynden-Bell & Kalnajs 1972). This is believed to be driven by transient spiral waves that heat the in-plane motions, although the process is not yet well understood. Long-term spiral arms produce no net effect. Remarkably, a single spiral wave near co-rotation can perturb the angular momentum of a star by ∼ 20% without significant heating: The star is simply moved from one circular orbit to another, inwards or outwards, by up to 2 kpc (Sellwood & Kosowsky 2000). Substantial variations in the angular momentum of a star are possible over its lifetime.

In addition to radial heating, stars experience vertical disk heating: Their vertical velocity dispersion increases as they age. This is believed to occur through a combination of in-plane spiral-arm heating and scattering off giant molecular clouds (e.g., Spitzer & Schwarzschild 1953, Carlberg & Sellwood 1985). The in-plane heating is most effective at the inner and outer Lindblad resonances and vanishes at corotation. 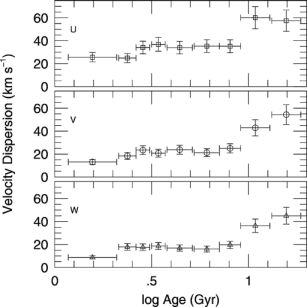In the vertical direction, an age-velocity dispersion relation is observed for stars younger than about 3 Ga, but older disk stars show a velocity dispersion that is independent of age (Figure 5). Thus, the vertical structure does depend on the mean age of the population for τ < 3 Ga (Edvardsson et al. 1993, confirmed from Hipparcos data by Gomez et al. 1997).

Figure 5. The relation between the three components of the velocity dispersion and the stellar age, as derived by Quillen & Garnett (2001) for stars from the sample of Edvardsson et al. (1993). Stars with ages between 2 and 10 Ga belong to the old thin disk: Their velocity dispersion is independent of age. The younger stars show a smaller velocity dispersion. The velocity dispersion doubles abruptly at an age of about 10 Ga; these older stars belong to the thick disk.

As the amplitude of the random motions increases, the star becomes less vulnerable to heating by transient spiral waves, and the heating process is expected to saturate. This probably happens after about 3 Ga (Binney & Lacey 1988, Jenkins & Binney 1990), consistent with observation. This is important for our purpose here. It means that dynamical information is preserved about the state of the thin disk at an early epoch, or roughly τ_L - 3 ≈ 7 Ga ago, for which τ_L is the look-back time when the disk first began to form.

The survival of old open clusters like NGC 6791, Berkeley 21 and Berkeley 17 (Friel 1995, van den Bergh 2000) is of interest here. The oldest open clusters exceed 10 Ga in age and constitute important fossils (Phelps & Janes 1996). Both old and young open clusters are part of the thin disk. If the heating perturbations occur over a lengthscale that significantly exceeds the size of an open cluster, it seems likely that the cluster will survive. A large spiral-arm heating event will heat many stars along their I_J trajectories. The trace of the heating event is likely to survive for a very long time but be visible only in integral space (Sellwood 2001). We note that vertical abundance gradients have not been seen among the open clusters (Friel & Janes 1993).

About 4% of disk stars are super metal-rich (SMR) relative to the Hyades (Castro et al. 1997). SMR stars of intermediate age appear to have formed a few kpc inside of the Solar circle from enriched gas. The oldest SMR stars appear to come from the Galactic Center: Their peculiar kinematics and outward migration may be associated with the central bar (Carraro et al. 1998, Grenon 1999).

In summary, our expectation is that fossil gradients within the disk are likely to be weak. This is borne out by observations of both the stars and the gas (Chiappini et al. 2001).

The vertical structure of the disk preserves another fossil – the thick disk – which we discuss in the next section. Like the open clusters, this component also does not show a vertical abundance gradient (Gilmore et al. 1995). In later sections, we argue that this may be the most important fossil to have survived the early stages of galaxy formation.

4.2.3. Disk heating by accretion: the thick disk

Heating from discrete accretion events also imposes vertical structure on the disk (Quinn & Goodman 1986, Walker et al. 1996). Such events can radically alter the structure of the inner disk and the bulge (see Figure 3d for an example) and are currently believed to have generated the thick disk of the Galaxy.

The galactic thick disk was first recognized by Gilmore & Reid (1983). It includes stars with a wide range of metallicity, from -2.2 ≤ [Fe/H] ≤ -0.5 (Chiba & Beers 2000): Most of the thick disk stars are in the more metal-rich end of this range. The velocity ellipsoid of the thick disk is observed to be (σ_R, σ_φ, σ_z = (46 ± 4, 50 ± 4, 35 ± 3) km s^-1 near the sun, with an asymmetric drift of about 30 km s^-1. For comparison, the nearby halo has a velocity ellipsoid (σ_R, σ_φ, σ_z = (141 ± 11, 106 ± 9, 94 ± 8) km s^-1 and its asymmetric drift is about 200 km s^-1.

The mean age of the thick disk is not known. From photometric age-dating of individual stars, the thick disk appears to be as old as the globular clusters. Indeed, the globular cluster 47 Tuc (age 12.5 ± 1.5 Ga; Liu & Chaboyer 2000) is often associated with the thick disk.

After Quinn & Goodman (1986), Walker et al. (1996) showed in detail that a low mass satellite could substantially heat the disk as it sinks rapidly within the potential well of a galaxy with a live halo. The conversion of satellite orbital energy to disk thermal energy is achieved through resonant scattering. Simulations of satellite accretion are important for understanding the survival of the thin disk and the origin of the thick disk. This is particularly relevant within the context of CDM. The satellites which do the damage are those that are dense enough to survive tidal disruption by the Galaxy. We note that even dwarf spheroidals which appear fluffy are in fact rather dense objects dominated by their dark matter (J. Kormendy & K. Freeman, in preparation).

It is fortuitous that the Galaxy has a thick disk, since this is not a generic phenomenon. The disk structure may be vertically stepped as a consequence of past discrete accretion events. The Edvardsson et al. (1993) data (Figure 5) appears to show an abrupt increase in the vertical component of the stellar velocity dispersion at an age of 10 Ga; see also Strömgren (1987). Freeman (1991) argued that the age−velocity dispersion relation shows three regimes: stars younger than 3 Ga with σ_z ∼ 10 km s^-1, stars between 3 and 10 Ga with σ_z ∼ 20 km s^-1, and stars older than 10 Ga with σ_z ∼ 40 km s^-1. The first regime probably arises from the disk heating process due to transient spiral arms which we described in the previous section. The last regime is the thick disk, presumably excited by an ancient discrete event.

Can we still identify the disrupting event that led to the thick disk? There is increasing evidence now that the globular cluster ω Cen is the stripped core of a dwarf elliptical (see “Globular Clusters” below). It is possible that the associated accretion event or an event like it was the event that triggered the thick disk to form.

In summary, it seems likely that the thick disk may provide a snap-frozen view of conditions in the disk shortly after the main epoch of dissipation. Any low level chemical or age gradients would be of great interest in the context of dissipation models. In this regard, Hartkopf & Yoss (1982) argued for the presence of a vertical abundance gradient in the thick disk, although Gilmore, Wyse & Jones (1995) found no such effect. Because stars of the thick disk spend relatively little time near the galactic plane, where the spiral arm heating and scattering by giant molecular clouds is most vigorous, radial mixing within the thick disk is unlikely to remove all vestiges of a gradient. If our earlier suggestions are right (see “Signatures of the Internal Distribution of Specific Angular Momentum” above), we might expect to see a different truncation radius for the thick disk compared to the thin disk.

4.2.4. Is there an age-metallicity relation?

Some fossil information has likely been preserved since the main epoch of baryon dissipation. The inner stellar bulge is a striking example. It is characterized by old, metal-rich stars, which seems to be at odds with the classical picture where metals accumulate with time (Tinsley 1980). However, the dynamical timescales in the inner bulge are very short compared to the outer disk and would have allowed for rapid enrichment at early times. This is consistent with the frequent occurrence of metal-rich cores of galaxies observed at high redshift (Hamann & Ferland 1999). The dynamical complexity of the Galactic bulge may not allow us to determine the sequence of events that gave rise to it. We anticipate that this will come about from far-field cosmology (Ellis et al. 2000).

The existence of an age-metallicity relation (AMR) in stars is a very important issue, about which there has long been disagreement. Twarog (1980), Meusinger et al. (1991) provide evidence for the presence of an AMR, while Carlberg et al. (1985) find that the metallicity of nearby F stars is approximately constant for stars older than about 4 Ga. More recently it has become clear that an AMR is apparent only in the solar neighborhood and is strictly true only for stars younger than 2 Ga and hotter than log T_eff = 3.8 (Feltzing et al. 2001). Edvardsson et al. (1993) demonstrate that there is no such relation for field stars in the old disk. Similarly, Friel (1995) shows that there is no AMR for open clusters (see “Open Clusters” below): she goes on to note that

Apparently, over the entire age of the disk, at any position in the disk, the oldest clusters form with compositions as enriched as those of much younger objects.

In fact, it has been recognized for a long time (e.g., Arp 1962, Eggen & Sandage 1969, Hirshfeld et al. 1978) that old, metal-rich stars permeate the galaxy, throughout the disk, the bulge and the halo. We regard the presence of old metal-rich stars as a first-order signature. An age-metallicity relation which applies to all stars would have been an important second-order signature, but we see no evidence for such a relation, except among the young stars.

4.2.5. Effects of environment and internal evolution

Environmental influences are operating on all scales of the hierarchy and across all stages of our signature classification, so our attempts to classify signatures are partly artificial. Within CDM, environmental effects persist throughout the life of the galaxy.

The parameters that govern the evolution of galaxies are among the key unknowns of modern astrophysics. Are the dominant influences internal (e.g., depth of potential) or external (e.g., environment) to galaxies? We consider here the effects of environment and internal evolution on the validity of the first-order signatures of galaxy formation (i.e., the properties that may have been conserved since the main epoch of baryon dissipation).

The well-known G dwarf problem indicates that external influences are important. A simple closed box model of chemical evolution predicts far too many metal-poor stars in the solar neighborhood (Tinsley 1980). This problem is easily remedied by allowing gas to flow into the region (Lacey & Fall 1983, 1985, Clayton 1987, 1988, Wyse & Silk 1989, Matteuci & Francois 1989, Worthey et al. 1996). In the context of CDM, this is believed to arise from the continued accretion of gas-rich dwarfs (e.g., Cole et al. 1994, Kauffmann & Charlot 1998).

Environment is clearly a key factor. Early type galaxies are highly clustered compared to late type galaxies (Hubble & Humason 1931, Dressler 1980). Trager et al. (2000) find that for a sample of early-type galaxies in low-density environments, there is a large spread in the Hβ index (i.e., age), but little variation in metallicity. For galaxies in the Fornax cluster, Kuntschner (2000) finds the opposite effect: A large spread in metallicity is present with little variation in age. This probably reflects strong differences in environment between the field and the cluster.

Another likely environmental effect is the fraction of S0 galaxies in clusters, which shows a rising trend with redshift since z ≈ 0.4 (Jones et al. 2000). Furthermore, S0 galaxies in the Ursa Major cluster show age gradients that are inverted compared to field spirals, in the sense that the cores are young and metal-rich (Tully et al. 1996, Kuntschner & Davies 1998). Both of these effects involve more recent phenomena and would be properly classified as second-order signatures.

Internal influences are also at work. A manifestation is the color-magnitude relation (CMR) in early-type (Sandage & Visvanathan 1978) and late-type (Peletier & de Grijs 1998) galaxies. The CMR does not arise from dust effects (Bell & de Jong 2000) and must reflect systematic variations in age and/or metallicity with luminosity. In the case of ellipticals, the CMR is believed to reflect a mass-metallicity dependence (Faber 1973, Bower et al. 1998). The relation is naturally explained by supernova-driven wind models in which more massive galaxies retain supernova ejecta and thus become more metal rich and redder (Larson 1974, Arimoto & Yoshii 1987). The CMR is presumably established during the main phase of baryon dissipation and is a genuine first-order signature.

Concannon et al. (2000) analyzed a sample of 100 early-type galaxies over a large range in mass. They found that lower-mass galaxies exhibit a larger range in age than higher-mass galaxies. This appears to show that smaller galaxies have had a more varied star formation history, which is at odds with the naive CDM picture of low-mass galaxies being older than high-mass galaxies (Baugh et al. 1996, Kauffman 1996). The work of Concannon et al. (2000) shows the presence of a real cosmic scatter in the star formation history. It is tempting to suggest that this cosmic scatter relates to different stages of evolution within the hierarchy. In this sense, we would regard the Concannon et al. result as a first-order manifestation of galaxy formation (see “Timescales and Fossils” above).

Spiral galaxies commonly show color gradients that presumably reflect gradients in age and metallicity (Peletier & de Grijs 1998). Faint spiral galaxies have younger ages and lower metallicities relative to bright spirals. In a study of 120 low-inclination spirals, Bell & de Jong (2000) found that the local surface density within galaxies is the most important parameter in shaping their star formation and chemical history. However, they find that metal-rich galaxies occur over the full range of surface density. This fact has a remarkable resonance with the distribution of the metal-rich open clusters that are found at any position in the Galactic disk (see “Is There an Age-Metallicity Relation?” above). Bell & de Jong argue that the total mass is a secondary factor that modulates the star formation history. Once again, these authors demonstrate the existence of cosmic scatter that may well arise from variations in environment.

4.3. Second Order Signatures – Major Processes Involved in Subsequent Evolution

4.3.1. Introduction

Here we consider relics of processes that have taken place in the Galaxy since most of the baryonic mass settled to the disk. There are several manifestations of these processes, probably the most significant of which is the star formation history of the disk, for which the open clusters are particularly important probes.

There is a wealth of detail relating to anomalous populations throughout the Galaxy, discussed at length by Majewski (1993). Examples include an excess of stars on extreme retrograde orbits (Norris & Ryan 1989, Carney et al. 1996), metal-poor halo stars of intermediate age (Preston et al. 1994) and metal-rich halo A stars (Rodgers et al. 1981).

In an earlier section, we discussed observational signatures of the CDM hierarchy in the Galactic context. In fact, detailed observations in velocity space are proving to be particularly useful in identifying structures that have long since dispersed in configuration space. In external galaxies, related structures are showing up as low surface brightness features. We do not know what role globular clusters play in the galaxy formation picture, but we include them here because at least one of them appears now to be the nucleus of a disrupted dwarf galaxy.

4.3.2. Star formation history

The star formation history (SFH) of our Galaxy has been very difficult to unravel. Derived star formation histories range from a roughly uniform star formation rate over the history of the disk to a SFH that was highly peaked at early times (e.g., Twarog 1980, Rocha-Pinto et al. 2000, Just 2001). Galaxies of the Local Group show a great diversity in SFH (Grebel 2001), although the average history over the Local Group appears consistent with the mean cosmic history (Hopkins et al. 2001). The present emphasis is on star formation studies that make use of the integrated properties of external galaxies, but it should be noted that this is necessarily weighted towards the most luminous populations. Key results for external galaxies are reviewed in “Effects of Environment and Internal Evolution” above. It was concluded that environmental effects are very significant in determining the SFH for individual galaxies.

The conventional approach to the study of chemical evolution in galaxy disks is to consider the solar neighborhood a closed box, and to assume that it is representative of all disks. Simple mathematical formulations have developed over the past 40 years (van den Bergh 1962, Schmidt 1963, Pagel & Patchett 1975, Talbot & Arnett 1971, Tinsley 1980, Twarog 1980, Pitts & Tayler 1989). Most observations are interpreted within this framework. The SFH is quantified in terms of stellar age, stellar (+gas) metallicity and, to a lesser extent, the existing gas fraction.

The use of broadband photometry coupled with stellar population synthesis is a well-established technique for probing the SFH of galaxy populations from integrated light. The power of the method is its simplicity, although it cannot uniquely disentangle the age-metallicity degeneracy (Bica et al. 1990, Charlot & Silk 1994).

Another widely used technique is the Lick index system (Burstein et al. 1984) further refined in Worthey et al. (1994), Trager et al. (1998). In this system, the Hβ index is the primary age-sensitive spectral indicator, whereas the Mg and Fe indices are the primary metallicity indicators. The Lick indices have well-known limitations: They correspond to low spectroscopic resolution (8−9 Å), require difficult corrections for internal galaxy motions, and are not calibrated onto a photometric scale. Furthermore, two of the most prominent Lick indices – Mg₂ λ5176 and Fe λ5270 – are now known to be susceptible to contamination from other elements, in particular Ca and C (Tripicco & Bell 1995).

How best to measure galaxy ages is a subject with a long history. The most reliable methods to date involve the low order transitions (n < 4) of the Balmer series. Ages derived from the Hγ equivalent width have been used by Jones & Worthey (1995). Rose (1994), Caldwell & Rose (1998) have pioneered the use of even higher-order Balmer lines to break the age-metallicity degeneracy (Worthey 1994). These higher-order lines are less affected by Balmer line emission from the interstellar medium. They develop a line ratio index Hn/Fe which is a sum over Hγ, Hδ and H8 lines with respect to local Fe lines. The most recent demonstration of the power of this index can be found in Concannon et al. (2000).

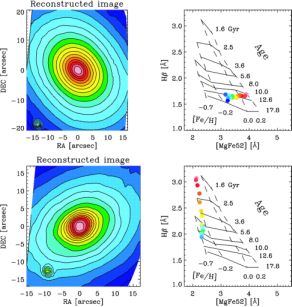
Ultimately, full spectrum fitting matched to spectral synthesis models holds the most promise (Vazdekis 1999). The new models, which have a fourfold increase in spectroscopic resolution compared to the Lick system, show that the isochrone or isochemical grid lines overlaid on a plot of two Lick indices are more orthogonal than the Worthey models. Thus, galaxies like NGC 4365 that exhibit no age gradient in the Vazdekis models (Davies et al. 2001; see Figure 6a) appear to show an age spread in the Worthey models. Interestingly, NGC 4150 exhibits an abundance spread with constant age (Figure 6b).

Figure 6. Sauron integral field observations of NGC 4365 (top panels) and NGC 4150 (bottom panels). Left panels: reconstructed surface brightness maps. Right panels: Hβ versus [MgFe5270] diagram. The points were derived from the Sauron datacubes by averaging along the corresponding color-coded isophotes (Bacon et al. 2001, Davies et al. 2001). The [Fe/H] vs. age grid is derived from Vazdekis (1999). [We acknowledge Harald Kuntschner and the Sauron team for these images.]

4.3.3. Low surface brightness structures in galaxies

Dynamical interaction between galaxies led to a range of structures including stellar shells (Malin & Carter 1980, Quinn 1984), fans (Weil et al. 1997), and tidal streamers (Gregg & West 1998, Calcaneo-Roldan et al. 2000, Zheng et al. 1999). Some excellent examples are shown in Figure 7. We see evidence of multiple nuclei, counter-rotating cores, and gas in polar orbits. At low light levels, the outermost stellar contours of spiral disks appear frequently to exhibit departures from axisymmetry (Rix & Zaritsky 1995). The same is true for spiral arms in all Hubble types (Schoenmakers et al. 1997; Cianci 2002).

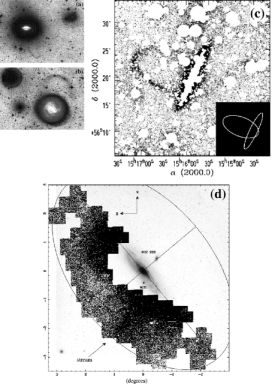
Figure 7. Examples of normal spirals with faint stellar streamers in the outer halo (see text): (a) M104 where the streamer is on a much larger scale than shown in Figure 3(c) (Malin & Hadley 1997); (b) M83 (Malin & Hadley 1997); (c) NGC 5907 (Shang et al. 1998); (d) M31 (Ibata et al. 2001a).

The stellar streamers are particularly interesting, as these may provide important constraints on galaxy models, particularly as kinematic measurements become possible through the detection of planetary nebulae. More than a dozen stellar streams are already known and this is probably indicative of a much larger population at very low surface brightness. Johnston et al. (2001) show that stellar streamers can survive for several gigayears and are only visible above the present optical detection limit (µ_V = 30 mag arcsec^-2) for roughly 4 × 10⁸ yr. A few galaxy groups (e.g., the Leo group) do show large-scale HI filaments that can remain visible for many Ga.

Deep CCD imaging has revealed a stellar loop around NGC 5907 (Shang et al. 1998) and a stellar feature extending from NGC 5548 (Tyson et al. 1998). The technique of photographic amplification has revealed stellar streamers in about ten sources (Malin & Hadley 1997, Calcaneo-Roldan et al. 2000, Weil et al. 1997). For these particular observations, the limiting surface brightness is µ_V ≈ 28.5 mag arcsec^-2. For all of these systems, we estimate that the total stream luminosities are in the range 3−20 × 10⁷ L_⊙.

In a recent development, wide-field CCD cameras have revealed stellar streamers through multiband photometry of millions of individual sources. A pointillist image can then be reconstructed in narrow color intervals so as to enhance features with respect to the field. This has led to the discovery of a stellar stream in M31 (Ibata et al. 2001a) and tidal tails extending from the globular cluster Pal 5 (Odenkirchen et al. 2001). This technique has the potential to push much deeper than the direct imaging method described above.

The low surface brightness universe is notoriously difficult to observe. Modern telescope and instrument designs are simply not optimized for this part of parameter space. Many claims of diffuse light detections in the neighborhood of galaxies have been shown to arise from scattered light internal to the instrument.

In “Structures in Phase Space,” below, we discuss moving groups identified within the Galaxy from proper motion and spectroscopic surveys. Their projected surface brightness is µ_V = 30−34 mag arcsec^-2, below the limit of modern imaging techniques.

Looking farther afield, we see evidence for discrete accretion events in the making. The Galaxy is encircled by satellite galaxies that appear confined to one or two great streams across the sky (Lynden-Bell & Lynden-Bell 1995). The most renowned of these are the Magellanic Clouds and the associated HI Magellanic stream. All of these are expected to merge with the Galaxy in the distant future, largely due to the dynamical friction from the extended halo.

4.3.4. Open clusters

In the context of near-field cosmology, we believe that the thick disk and the old open clusters of the thin disk are among the most important diagnostics. The open clusters are the subject of an outstanding and comprehensive review by Friel (1995). Here, we summarize the properties that are most important for our purpose.

Both old and young clusters are part of the thin disk. Their key attribute is that they provide a direct time line for investigating change, which we explore in “The Gaiasphere and the Limits of Knowledge,” below. The oldest open clusters exceed 10 Ga in age and constitute important fossils (Phelps & Janes 1996). In “Can disks preserve fossil information,” we noted that the survival of these fossil clusters is an interesting issue in its own right. Friel (1995) finds no old open clusters within a galactocentric radius of 7 kpc; these are likely to have disrupted or migrated out of the central regions (van den Bergh & McClure 1980). It has long been recognized that open clusters walk a knife edge between survival and disruption (King 1958a, b, c).

Like field stars in the disk, Janes & Phelps (1994) find that the old cluster population (relative to Hyades) is defined by a 375-pc scale height exponential distribution, whereas young clusters have a 55-pc scale height (Figure 8a,b). Again, like the field stars, vertical abundance gradients have not been seen in open clusters (Friel & Janes 1993), although radial gradients are well established (Friel 1995, van den Bergh 2000). For old open clusters, Twarog et al. (1997) claim evidence for a stepped radial metallicity distribution where [Fe/H] ≈ 0 within 10 kpc, falling to [Fe/H] ≈ -0.3 in the outer disk. However, this effect is not seen in young objects, e.g., HII regions and B stars (Henry 1998).

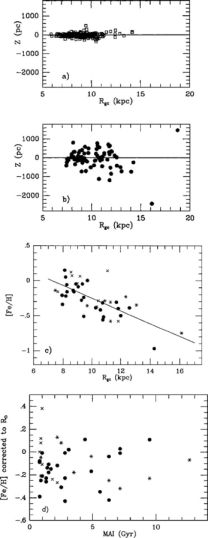
Figure 8. (a) The distribution of open clusters younger than Hyades with height from the plane as a function of Galactocentric distance Rgc (Friel 1995). The Sun is at 8.5 kpc. (b) The distribution of clusters with ages equal to or greater than the Hyades. (c) The open clusters exhibit a well-defined abundance gradient. (d) There is no discernible age-metallicity relation (AMR) when the cluster abundances are corrected for the radial abundance gradient.

In Figure 8c, both the old and young open clusters show essentially the same radial trend in metallicity. After reviewing the available observations, Friel (1995) finds no evidence for an age-metallicity relation for open clusters (Figure 8d). In agreement with Eggen & Sandage (1969), she notes that over the entire age of the disk, at any position in the disk, the oldest clusters form with compositions as enriched as those of much younger objects.

These remarkable observations appear to indicate that shortly after the main epoch of baryon dissipation, the thin disk was established at least as far out as 15 kpc. The oldest open clusters approach the age of the thick disk. Since, in “Disk Heating by Accretion,” we noted that the thick disk is likely to be a snap frozen picture of the thin disk shortly after disk formation, we would expect the truncation of the thick disk (see “Signatures of Global Quantities,” above) to reflect the extent of the thin disk at the epoch of the event that puffed up the thick disk.

4.3.5. Globular clusters

We have long suspected that globular clusters are the fossil remnants of violent processes in the protogalactic era (Peebles & Dicke 1968). But there is a growing suspicion that globulars are telling us more about globulars than galactic origins (Harris 2001). The Milky Way has about 150 globular clusters with 20% lying within a few kiloparsecs of the Galactic Center. They constitute a negligible fraction of the light and mass (2%) of the stellar halo today. Their significance rests in their age. The oldest globular clusters in the outer halo have an age of 13 ± 2.5 Ga (90% confidence).

The ages of the oldest globular clusters in the inner and outer halo, the Large Magellanic Cloud and the nearby Fornax and Sgr dwarf spheroidal galaxies show a remarkable uniformity. To a precision of ± 1 Ga, the onset of globular cluster formation was well synchronized over a volume centered on our Galaxy with a radius > 100 kpc (Da Costa 1999).

Globular cluster stars are older than the oldest disk stars, e.g., white dwarfs and the oldest red giants. These clusters are also more metal poor than the underlying halo light in all galaxies and at all radii (Harris 1991), but again there are exceptions to the rule. Since Morgan's (1950) and Kinman's (1959) classic work, we have known that there are two distinct populations of globular clusters in the Galaxy. The properties that we associate with these two populations today were derived by Zinn (1985) who showed that they have very different structure, kinematics and metallicities. The halo population is metal poor ([Fe/H] < -0.8) and slowly rotating with a roughly spherical distribution; the disk population is metal rich ([Fe/H] > -0.8) and in rapid rotation.

A major development has been the discovery of young globular clusters in disturbed or interacting galaxies, e.g., NGC 1275 (Holtzman et al. 1992), NGC 7252 (Whitmore et al. 1993) and the Antennae (Whitmore & Schweizer 1995). Schweizer (1987) first suspected that globular clusters were formed in mergers. Later, Ashman & Zepf (1992) predicted that the HST would reveal young globular clusters through their compact sizes, high luminosities and blue colors. The very high internal densities of globular clusters today must partly reflect the conditions when they were formed. Harris & Pudritz (1994) present a model for globular clusters produced in fragmenting giant molecular clouds, which are of the right mass and density range to resemble accretion fragments in the Searle-Zinn model.

Globular clusters have been elegantly referred to as “canaries in a coal mine” (Arras & Wasserman 1999). They are subject to a range of disruptive effects, including two-body relaxation and erosion by the tidal field of their host galaxy, and the tidal shocking that they experience as their orbits take them through the galactic disk and substructure in the dark halo. In addition to self-destruction through stellar mass loss, tidal shocking may have been very important in the early universe (Gnedin et al. 1999). If globular clusters originally formed in great numbers, the disrupted clusters may now contribute to the stellar halo (Norris & Ryan 1989, Oort 1965). Halo field stars and globular clusters in the Milky Way have similar mean metallicities (Carney 1993); however, the metallicity distribution of the halo field stars extends to much lower metallicity ([Fe/H] ≃ -5) than that of the globular clusters ([Fe/H] ≃ -2.2). We note again the remarkable similarity in the metallicity range of the globular clusters and the thick disk (-2.2 ≲ [Fe/H] ≲ -0.5).

In the nucleated dwarf elliptical galaxies (Binggeli et al. 1985), the nucleus typically provides about 1% of the total luminosity; globular clusters could be considered as the stripped nuclei of these satellite objects without exceeding the visible halo mass (Zinnecker & Cannon 1986, Freeman 1993). It is an intriguing prospect that the existing globular clusters could be the stripped relicts of an ancient swarm of protogalactic stellar fragments, i.e., the original building blocks of the Universe.

In the Searle-Zinn picture, globular clusters are intimately linked to gas-rich, protogalactic infalling fragments. Multiple stellar populations have recently been detected in ω Cen, the most massive cluster in the Galaxy (Lee et al. 1999). How did ω Cen retain its gas for a later burst? It now appears that it was associated with a gas-rich dwarf, either as an in situ cluster or as the stellar nucleus. The present-day cluster density is sufficiently high that it would have survived tidal disruption by the Galaxy, unlike the more diffuse envelope of this dwarf galaxy. The very bound retrograde orbit supports the view that ω Cen entered the Galaxy as part of a more massive system whose orbit decayed through dynamical friction.

If globular clusters are so ancient, why are the abundances of the most metal-poor population as high as they are? Because it does not take much star formation to increase the metal abundance up to [Fe/H] = -1.5 (Frayer & Brown 1997), the cluster abundances may reflect low levels of star formation even before the first (dark + baryon) systems came together.

Old age is not necessarily associated with low metallicity (compare “Timescales and Fossils” above). We recall that CO has been detected at z ∼ 5 (Yun et al. 2000). Hamann & Ferland (1999) demonstrate that stellar populations at the highest redshift currently observed appear to have solar or super-solar metallicity. We believe that there is no mystery about high abundances at high redshift. The dynamical times in the cores of these systems are short, so there has been time for multiple generations of star formation and chemical enrichment. In this sense, the cores of high redshift galaxies need not be relevant to the chemical properties of the globular clusters, although both kinds of objects were probably formed at about the same time.

The first generation of globular clusters may have been produced in merger-driven starbursts when the primordial fragments came together for the first time. If at least some fragments retained some of their identity while the halo was formed, a small number of enrichment events per fragment would ensure a Poissonian scatter in properties between globular clusters, and multiple populations within individual clusters (Searle & Zinn 1978).

4.3.6. Structures in phase space

One class of systems that exhibit coherence in velocity space are the open clusters associated with the disk. Here the common space motion of the stars with respect to the Sun is perceived as a convergence of the proper motions to a single point (strictly speaking, minimum volume) on the sky (Boss 1908; see de Zeeuw et al. 1999 for a recent application). More than a dozen such systems have been identified this way. However, these are all young open clusters largely associated with the Gould belt. With sufficiently precise kinematics, it may be possible to identify open clusters that have recently dispersed, particularly if the group is confined to a specific radial zone by resonances in the outer disk. For example, Feltzing & Holmberg (2000) show that the metal-rich ([Fe/H] ≈ 0.2) moving group HR 1614, thought to be 2 Ga old, can be identified in the Hipparcos data set.

Recently, attention has turned to a diverse set of moving groups that are thought to be associated with the stellar halo and in some instances are clearly fossils associated with accretion events in the distant past. The evidence for these groups dates back to the discovery of the halo itself. Shortly before the publication of the landmark ELS paper, Eggen & Sandage (1959) discovered that the nearby high-velocity star, Groombridge 1830, belongs to a moving group now passing through the Galactic disk.

In a long series of papers, Eggen went on to identify a number of moving groups, some of which appear to encompass the solar neighborhood, and others that may be associated with the halo. The relevant references are given by Taylor (2000). Various authors have noted that many of the groups are difficult to confirm (Griffin 1998, Taylor 2000). More systematic surveys over the past few decades have identified a number of moving populations associated with the halo (Freeman 1987, Majewksi 1993), although the reality of some of these groups is still debated. The reality of these groups is of paramount importance in the context of halo formation. Majewski et al. (1996) suspect that much or all of the halo could exhibit phase-space clumping with data of sufficient quality.

In recent years, the existence of kinematic sub-structure in the galactic halo has become clear. Helmi et al. (1999) identified 88 metal-poor stars within 1 kiloparsec of the Sun from the Hipparcos astrometric catalogue. After deducing accurate 3-D space motions, they found a highly significant group of 8 stars that appear clumped in phase space and confined to a highly inclined orbit.

The most dramatic evidence is surely the highly disrupted Sgr dwarf galaxy identified by Ibata et al. (1994, 1995). These authors used multi-object spectroscopy to uncover an elongated stellar stream moving through the plane on the far side of the Galaxy. The Sgr dwarf is a low mass dwarf spheroidal galaxy about 25 kpc from the Sun that is presently being disrupted by the Galactic tidal field. The long axis of the prolate body (axis ratios ∼ 3:1:1) is about 10 kpc, oriented perpendicular to the Galactic plane along ℓ = 6^∘ and centered at b = -15^∘. Sgr contains a mix of stellar populations, an extended dark halo (mass ≥ 10⁹ M_⊙) and at least four globular clusters (Ibata et al. 1997). The Sgr stream has since been recovered by several photometric surveys (Vivas et al. 2001, Newberg et al. 2002, Ibata et al. 2001c).

N-body simulations have shown that stellar streams are formed when low mass systems are accreted by a large galaxy (e.g., Harding et al. 2001). Streamers remain dynamically cold and identifiable as a kinematic substructure long after they have ceased to be recognizable in star counts against the vast stellar background of the galaxy (Tremaine 1993, Ibata & Lewis 1998, Johnston 1998, Helmi & White 1999).

Within the Galaxy, moving groups can be identified with even limited phase-space information (de Bruijne 1999, de Zeeuw et al. 1999). This also holds for satellites orbiting within the spherical halo, since the debris remains in the plane of motion for at least a few orbits (Lynden-Bell & Lynden-Bell 1995, Johnston et al. 1996). But a satellite experiencing the disk potential no longer conserves its angular momentum and its orbit plane undergoes strong precession (Helmi & White 1999). In Figure 9, we show the sky projection of a satellite 8 Ga after disruption. These more complex structures are usually highly localized and therefore easy to recognize in the space of conserved quantities like energy and angular momentum for individual stars.

Figure 9. A satellite in orbit about the Milky Way as it would appear after 8 Ga. While stars from the disrupted satellite appear to be dispersed over a very wide region of sky, it will be possible to deduce the parameters of the original event using special techniques (see text). (We acknowledge A. Helmi and S. White for this image.

The evolution in phase space of a disrupting satellite is well behaved as its stars become phase mixed. Its phase space flow obeys Liouville's theorem, i.e., the flow is incompressible. Highly intuitive accounts are given elsewhere (Carlberg 1986, Tremaine 1999, Hernquist & Quinn 1988). It should be possible to recognize partially phase-mixed structures that cover the observed space, although special techniques are needed to find them.

Four astrometric space missions are planned for the next decade. These are the proposed German DIVA mission (∼ 2003); the FAME mission (∼ 2005) and the pointed SIM mission (∼ 2005); and the ESA Gaia mission (∼ 2009) which will observe a billion stars to V ∼ 20, with accuracy 10µas at a V ∼ 15. The web sites for these missions are at: http://www.ari.uni-heidelberg.de/diva/, http://aa.usno.navy.mil/FAME/, http://sim.jpl.nasa.gov/, http://sci.esa.int/gaia/.

The astrometric missions will derive 6-dimensional phase space coordinates and spectrophotometric properties for millions of stars within a 20 kiloparsec sphere – the Gaiasphere. The ambitious Gaia mission will obtain distances for up to 90 million stars with better than 5% accuracy, and measure proper motions with an accuracy approaching microarcsec per year. If hierarchical CDM is correct, there should be thousands of coherent streamers that make up the outer halo, and hundreds of partially phase-mixed structures within the inner halo. A satellite experiencing the disk potential no longer conserves its angular momentum and its orbit plane undergoes strong precession (see Figure 10c,d). In Figure 10a,b, Helmi et al. (1999) demonstrate the relative ease with which Gaia will identify substructure within the stellar halo.

Figure 10. (a) Initial distribution of particles for 33 systems falling into the Galactic halo in integral of motion space. (b) The final distribution of particles in (a) after 12 Ga; the data points have been convolved with the errors expected for Gaia. [We acknowledge A. Helmi for these images.] (c) A simulation of the baryon halo built up through accretion of 100 satellite galaxies. The different colors show the disrupted remnants of individual satellites. (d) This is the same simulation shown in a different coordinate frame, i.e., the orbit radius (horizontal) plotted against the observed radial velocity (vertical) of the star. [We acknowledge P. Harding and H. Morrison for these images.]