


The COBE DMR measurement of CMB anisotropy on the 10° angular scale and determination of the primeval deuterium abundance served to mark the beginning of a new era of precision cosmology. Overnight, COBE changed the study of large-scale structure: for theories like inflation and defects which specify the shape of the spectrum of density perturbations, the COBE measurement fixed the level of inhomogeneity on all scales to an accuracy of around 10%. Likewise, the measurement of the primeval deuterium abundance, led to a 10% determination of the baryon density.
Within the next few years, an avalanche of data, driven by advances in technology, promises definitive independent observations of the geometry, mass distribution and composition, and detailed structure of the Universe. In a radical departure from its history, cosmology is becoming an exact science. These new observations span the wavelength range from microwave to gamma rays and beyond, and utilize techniques as varied as CMB microwave interferometry, faint supernova photometry and spectroscopy, gravitational lensing, and massive photometric and spectroscopic surveys of millions of galaxies.
The COBE measurement of CMB anisotropy on angular scales
from around 10° to 100° yielded a precise determination of
the amplitude of mass fluctuations on very large scales, 103
Mpc-104 Mpc. A host of experiments will view the CMB with
much higher angular resolution and more precision than COBE,
culminating in the two satellite experiments, NASA's MAP and
ESA's Planck Surveyor, which will map the full sky to an
angular resolution of 0.1°. In so doing, the mass distribution
in the Universe at a simpler time, before nonlinear structures
had formed, will be determined on scales from 104 Mpc down to
10 Mpc. (Temperature fluctuations on angular scale  arise from density
fluctuations on length scales L ~ 100h-1 Mpc [
arise from density
fluctuations on length scales L ~ 100h-1 Mpc [ / deg];
fluctuations on scales ~ 1 Mpc give rise to galaxies, on scales
~ 10 Mpc give rise to clusters, and on scales ~ 100 Mpc give
rise to great walls.)
/ deg];
fluctuations on scales ~ 1 Mpc give rise to galaxies, on scales
~ 10 Mpc give rise to clusters, and on scales ~ 100 Mpc give
rise to great walls.)
The multipole power spectrum of CMB temperature fluctuations
has a rich structure and encodes a wealth of information about
the Universe. The peaks in the power spectrum
are caused by baryon-photon oscillations, which are driven
by the gravitational force of the dark matter. Since
decoupling is essentially instantaneous, different Fourier modes
are caught at different phases, which is reflected in a multipole
spectrum of anisotropy (see Fig. 5).
The existence of the first peak is evident.
If the satellite missions are as successful as cosmologists
hope, and if foregrounds (e.g., diffuse emission from our own galaxy
and extragalactic point sources) are not a serious problem,
it should be possible to use the measured multipole power
spectrum to determine
 0 and many other
cosmological parameters (e.g.,
0 and many other
cosmological parameters (e.g.,  Bh2,
h, n, level of gravitational waves,
Bh2,
h, n, level of gravitational waves, 
 , and
, and

 ) to precision of 1% or better in some cases
(see
Wilkinson 1999).
) to precision of 1% or better in some cases
(see
Wilkinson 1999).
Another impressive map is in the works. The present 3-dimensional structure of the local Universe will also be mapped to unprecedented precision in the next few years by the Sloan Digital Sky Survey (SDSS) (see Gunn et al. 1998), which will obtain the redshifts of a million galaxies over 25% of the northern sky out to redshift z ~ 0.1, and the Two-degree Field Survey (2dF), which will collect 250,000 redshifts in many 2° patches of the southern sky (Colless 1988). These surveys will cover around 0.1% of the observable Universe, and more importantly, will map structure out to scales of about 500h-1 Mpc, well beyond the size of the largest structures known. This should be large enough to provide a typical sample of the Universe. The two maps - CMB snapshot of the Universe at 300,000 yrs and the SDSS map of the Universe today - when used together have enormous leverage to test cosmological models and determine cosmological parameters.
Several projects are underway to map smaller, more distant parts of the Universe to study the ``recent'' evolution of galaxies and structure. Using a new large spectrograph, the 10-meter Keck telescope will begin to map galaxies in smaller fields on the sky out to redshifts of 4 or so. Ultimately, the Next Generation Space Telescope, which is likely to have an 8-meter mirror and capability in the infrared (most of the light of high-redshift galaxies has been shifted into the infrared) will probe the first generation of stars and galaxies.
Much of our current understanding of the Universe is based on the
assumption that light traces mass, because telescopes detect light
and not mass. There is some evidence that light is not a terribly
``biased'' tracer of mass, at least on the scales of galaxies. However,
it would be a convenient accident if the mass-to-light ratio
were universal. It is possible that there is a lot of undiscovered
matter, perhaps even enough to bring  M to unity,
associated with dim galaxies or other mass concentrations that are
not correlated with bright galaxies.
M to unity,
associated with dim galaxies or other mass concentrations that are
not correlated with bright galaxies.
Gravitational lensing is a powerful means of measuring cosmic mass overdensities in the linear regime directly (see e.g., Blandford & Narayan 1992; Tyson 1993): dark matter overdensities at moderate redshift (z ~ 0.2-0.5) systematically distort background galaxy images (referred to as weak gravitational lensing). A typical random one-square-degree patch of the sky contains a million faint high-redshift galaxies. Using these galaxies, weak gravitational lensing may be used to map the intervening dark matter overdensities directly. This technique has been used to map known or suspected mass concentrations in clusters of galaxies over redshifts 0.1 < z < 0.8 (see Fig. 8 and Clowe et al. 1998) and only recently has been applied to random fields. Large mosaics of CCDs make this kind of direct mass survey possible, and results from these surveys are expected in the coming years.
Crucial to taking advantage of the advances in our understanding of the distribution of matter in the Universe and the formation of galaxies are the numerical simulations that link theory with observation. Simulations now involve billions of particles, allowing a dynamical range of a factor of one thousand (see Fig. 12). Many simulations now involve not only gravity, but the hydrodynamics of the baryons. Advances in computing have been crucial.

|
Figure 12. One of the largest simulations
of the development of
structure in the Universe. (from
Virgo Collaboration
1998).
Shown here is projected mass in a |
Impressive progress has been made toward measuring the cosmological parameters H0, q0 and t0, and more progress is on the horizon. A 5% or better measurement of the Hubble constant on scales that are a substantial fraction of the distance across the Universe may be within our grasp. Techniques that do not rely upon phenomenological standard candles are beginning to play an important role. The time delay of a flare event seen in the multiple images of a lensed quasar is related only to the redshifts of the lens and quasar, the lens magnification, the angular separation of the quasar images, and the Hubble constant. Thanks to a recent flare, an accurate time delay between the two images of the gravitationally lensed quasar Q0957+561 has been reliably determined, but the lens itself must be mapped before H0 is precisely determined (Kundic et al. 1997). This technique is being applied to other lensed quasar systems as well. The pattern of CMB anisotropy has great potential to accurately determine H0. Another technique (Sunyaev-Zel'dovich, or SZ), which uses the small distortion of the CMB when viewed through a cluster containing hot gas (due to Compton up-scattering of CMB photons), has begun to produce reliable numbers (Birkinshaw 1998).
Currently, the largest gap in our knowledge of the mass content of
the Universe is identifying the bulk of the matter density,  ?
=
?
=  M -
M -  B ~ 0.3. The most
compelling idea is that
this component consists of relic elementary particles, such as
neutralinos, axions or neutrinos. If such particles compose most
of the dark matter, then they should account for most of the
dark matter in the halo of our own galaxy and have a local mass
density of around 10-24 g cm-3. Several laboratory
experiments are
currently running with sufficient sensitivity to search directly
for neutralinos of mass 10 GeV - 500 GeV and cross-section that is
motivated by the minimal supersymmetric standard model. While the
supersymmetric parameter space spans more than 3 orders-of-magnitude
in cross section, even greater sensitivities are expected in the
near future. These experiments involve high-sensitivity, low-background
detectors designed to detect the small (order keV) recoil energy
when a neutralino elastically scatters off a nucleus in the detector;
the small rates (less than one scattering per day per kg of detector)
add to the challenge
(Sadoulet 1999).
B ~ 0.3. The most
compelling idea is that
this component consists of relic elementary particles, such as
neutralinos, axions or neutrinos. If such particles compose most
of the dark matter, then they should account for most of the
dark matter in the halo of our own galaxy and have a local mass
density of around 10-24 g cm-3. Several laboratory
experiments are
currently running with sufficient sensitivity to search directly
for neutralinos of mass 10 GeV - 500 GeV and cross-section that is
motivated by the minimal supersymmetric standard model. While the
supersymmetric parameter space spans more than 3 orders-of-magnitude
in cross section, even greater sensitivities are expected in the
near future. These experiments involve high-sensitivity, low-background
detectors designed to detect the small (order keV) recoil energy
when a neutralino elastically scatters off a nucleus in the detector;
the small rates (less than one scattering per day per kg of detector)
add to the challenge
(Sadoulet 1999).
An axion detector has achieved sufficient sensitivity to detect halo axions, and is searching the mass range 10-6 eV - 10-5 eV where axions would contribute significantly to the mass density. This detector, based upon the conversion of axions to photons in strong magnetic field, consists of a hi-Q cavity immersed in a 7 Tesla magnetic field and is operating with a sensitivity of 10-23 W in the GHz frequency range. Within five years it is hoped that the entire theoretically favored mass range will be explored (Rosenberg 1998).
While light neutrinos are no longer favored by cosmologists for the dark matter, as they would lead to structure in the Universe that is not consistent with what we see today, because of their large numbers, 113 cm-3, they could be an important component of mass density even if only one species has a tiny mass:
Even with a mass as small as one
eV neutrinos would make an imprint on the structure of the Universe
that is potentially detectable.
Particle theorists strongly favor the idea that neutrinos
have small, but nonzero mass, and the see-saw mechanism can
explain why their masses are so much smaller than the
other quarks and leptons: m
Super-K detects neutrinos from the sun
and those produced in the earth's atmosphere by cosmic-ray interactions.
For several years now the solar-neutrino data has shown evidence
for neutrino oscillations, corresponding to a neutrino mass-difference
squared of around 10-5 eV2 or 10-10
eV2, too small
to be of cosmological interest (unless two neutrino species are
nearly degenerate in mass.) The Super-K collaboration recently
announced evidence for neutrino oscillations based upon the atmospheric
neutrino data. Their results, which indicate a mass-difference squared of
around 10-3-10-2 eV2
(Fukuda et al. 1998)
and imply at least one
neutrino has a mass of order 0.1 eV or larger, are
much more interesting cosmologically. Over the next decade
particle physicists will pursue neutrino mass with a host of new
experiments, characterized by very long baselines (neutrino source
and detector separated by hundreds of kilometers) and should clarify
the situation.
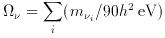
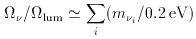
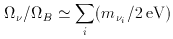
 ~ m2q, l / M where
M ~ 1010 GeV - 1015 GeV is the very large mass
of the right-handed partner(s) of the usual left-handed
neutrinos (see e.g.,
Schwarz & Seiberg 1999).
Because neutrino masses are a fundamental prediction
of unified field theories, much effort is directed at probing
neutrino masses. The majority of experiments now involve
looking for the oscillation of one neutrino species into
another, which is only possible if neutrinos have mass.
These experiments are carried out at accelerators, at nuclear
reactors, and in large-underground detectors such as Super-Kamiokande
and the SNO facility.
~ m2q, l / M where
M ~ 1010 GeV - 1015 GeV is the very large mass
of the right-handed partner(s) of the usual left-handed
neutrinos (see e.g.,
Schwarz & Seiberg 1999).
Because neutrino masses are a fundamental prediction
of unified field theories, much effort is directed at probing
neutrino masses. The majority of experiments now involve
looking for the oscillation of one neutrino species into
another, which is only possible if neutrinos have mass.
These experiments are carried out at accelerators, at nuclear
reactors, and in large-underground detectors such as Super-Kamiokande
and the SNO facility.