


D. Energetics
Before redshift measurements were available the GRB energy was estimated from the BATSE catalogue by fitting an (isotropic) luminosity function to the flux distribution (see e.g Cohen and Piran [56], Guetta et al. [153], Loredo and Wasserman [225], Schmidt [379, 380, 381] and many others). This lead to a statistical estimate of the luminosity function of a distribution of bursts.
These estimates were revolutionized with the direct determination
of the redshift for individual bursts. Now the energy could be
estimated directly for specific bursts. Given an observed
 -ray
fluence and the redshift to a burst one can easily
estimate the energy emitted in
-ray
fluence and the redshift to a burst one can easily
estimate the energy emitted in
 -rays,
E
-rays,
E , iso
assuming that the emission is isotropic (see
Bloom et al.
[35]
for a detailed study including k corrections). The inferred energy,
E
, iso
assuming that the emission is isotropic (see
Bloom et al.
[35]
for a detailed study including k corrections). The inferred energy,
E , iso was the
isotropic energy, namely the energy assuming that the GRB emission
is isotropic in all directions. The energy of the first burst with
a determined redshift, GRB 970508, was around 1051 ergs.
However, as afterglow observations proceeded, alarmingly large
values (e.g. 3.4 × 1054ergs for GRB 990123) were
measured for E
, iso was the
isotropic energy, namely the energy assuming that the GRB emission
is isotropic in all directions. The energy of the first burst with
a determined redshift, GRB 970508, was around 1051 ergs.
However, as afterglow observations proceeded, alarmingly large
values (e.g. 3.4 × 1054ergs for GRB 990123) were
measured for E , iso. The variance was around three
orders of magnitude.
, iso. The variance was around three
orders of magnitude.
However, it turned out
[344,
374]
that GRBs are beamed
and E , iso would not then be a good estimate for the
total energy emitted in
, iso would not then be a good estimate for the
total energy emitted in
 -rays.
Instead: E
-rays.
Instead: E
 (
( 2 / 2)
E
2 / 2)
E , iso. The angle,
, iso. The angle,
 , is the effective
angle of
, is the effective
angle of
 -ray
emission. It can be estimated from tb,
the time of the break in the afterglow light curve
[374]:
-ray
emission. It can be estimated from tb,
the time of the break in the afterglow light curve
[374]:
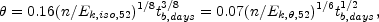 |
(4) |
where tb, days is the break time in days.
Ek, iso, 52 is
"isotropic equivalent" kinetic energy, discussed below, in units
of 1052 ergs, while
Ek, , 52
is the real kinetic energy in the jet i.e:
Ek,
, 52
is the real kinetic energy in the jet i.e:
Ek, , 52
= (
, 52
= ( 2 /
2)Ek, iso, 52. One has to be careful which of the two
energies one discusses. In the following I will usually consider, unless
specifically mentioned differently, Ek, iso, 52, which
is also related to the energy per unit solid angle as:
Ek, iso, 52 /
4
2 /
2)Ek, iso, 52. One has to be careful which of the two
energies one discusses. In the following I will usually consider, unless
specifically mentioned differently, Ek, iso, 52, which
is also related to the energy per unit solid angle as:
Ek, iso, 52 /
4 . The jet break is observed
both in the optical and in the
radio frequencies. Note that the the observational signature in
the radio differs from that at optical and X-ray
[159,
374]
(see Fig. 25) and
this provides an additional confirmation for this interpretation.
. The jet break is observed
both in the optical and in the
radio frequencies. Note that the the observational signature in
the radio differs from that at optical and X-ray
[159,
374]
(see Fig. 25) and
this provides an additional confirmation for this interpretation.
Frail et al.
[105]
estimated E for 18 bursts, finding
typical values around 1051 ergs (see also
Panaitescu and Kumar
[291]).
Bloom et al.
[34]
find E
for 18 bursts, finding
typical values around 1051 ergs (see also
Panaitescu and Kumar
[291]).
Bloom et al.
[34]
find E = 1.33 × 1051
h65-2 erg and a
burst-to-burst variance about this value ~ 0.35 dex, a
factor of 2.2. This is three orders of magnitude smaller than the
variance in the isotropic equivalent E
= 1.33 × 1051
h65-2 erg and a
burst-to-burst variance about this value ~ 0.35 dex, a
factor of 2.2. This is three orders of magnitude smaller than the
variance in the isotropic equivalent E . A
compilation of the beamed energies from
[34], is shown in
Figs 12 and 13. It
demonstrates
nicely this phenomenon. The constancy of E
. A
compilation of the beamed energies from
[34], is shown in
Figs 12 and 13. It
demonstrates
nicely this phenomenon. The constancy of E is
remarkable, as it involves a product of a factor inferred from the GRB
observation (the
is
remarkable, as it involves a product of a factor inferred from the GRB
observation (the  -rays flux) with a factor inferred from the
afterglow observations (the jet opening angle). However,
E
-rays flux) with a factor inferred from the
afterglow observations (the jet opening angle). However,
E might not be a good estimate for
Etot, the total energy emitted by the central
engine. First, an unknown conversion efficiency of energy to
might not be a good estimate for
Etot, the total energy emitted by the central
engine. First, an unknown conversion efficiency of energy to
 -rays has
to be considered: Etot =
-rays has
to be considered: Etot =
 -1
E
-1
E =
=
 -1(
-1( 2 / 2)
E
2 / 2)
E , iso. Second, the large Lorentz factor during the
, iso. Second, the large Lorentz factor during the
 -ray
emission phase, makes the observed
E
-ray
emission phase, makes the observed
E rather
sensitive to angular inhomogeneities of the relativistic ejecta
[206].
The recent early observations of the afterglow of GRB 021004 indicate
that indeed a significant angular variability of this kind exists
[271,
274].
rather
sensitive to angular inhomogeneities of the relativistic ejecta
[206].
The recent early observations of the afterglow of GRB 021004 indicate
that indeed a significant angular variability of this kind exists
[271,
274].
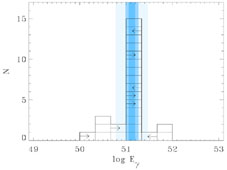 |
Figure 12. A histogram of
GRB energies (E |
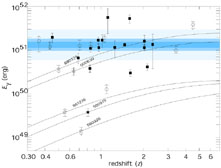 |
Figure 13. GRB energy
release versus redshift. Bands of 1, 2, and 5
|
The kinetic energy of the flow during the adiabatic afterglow
phase, Ek is yet another energy measure that arises. This
energy (per unit solid angle) can be estimated from the afterglow
light curve and spectra. Specifically it is rather closely
related to the observed afterglow X-ray flux
[109,
201,
310].
As this energy is measured when the Lorentz factor is smaller it is less
sensitive than E to angular variability. The constancy of
the X-ray flux
[310]
suggest that this energy is also constant. Estimates of
Ek,
to angular variability. The constancy of
the X-ray flux
[310]
suggest that this energy is also constant. Estimates of
Ek, [291]
show that
[291]
show that 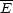

 3
3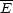 k,
k,  , namely the
observed "beamed" GRB energy is larger than the estimated
"beamed" kinetic energy of the afterglow. Frail et al.
[105],
however, find that
, namely the
observed "beamed" GRB energy is larger than the estimated
"beamed" kinetic energy of the afterglow. Frail et al.
[105],
however, find that
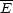


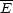 k,
k,  ,
namely that the two energies are comparable.
,
namely that the two energies are comparable.
An alternative interpretation to the observed breaks is that we
are viewing a "universal" angle dependent, namely, "structured"
jet - from different viewing angles
[219,
347,
446].
The observed break corresponds in this model to the observing angle
 and not
to the opening angle of the jet. This interpretation means that
the GRB beams are wide and hence the rate of GRBs is smaller than
the rate implied by the usual beaming factor. On the other hand it
implies that GRBs are more energetic.
Guetta et al.
[153]
estimate that this factor (the
ratio of the fixed energy of a "structured" jet relative to the
energy of a uniform jet to be ~ 7. However they find that the
observing angle distribution is somewhat inconsistent with the
simple geometric one that should arise in universal structured
jets (see also Nakar et al.
[266],
Perna et al.
[299]).
The energy-angle relation discussed earlier require (see
Section VIII below) an angle dependent jet
with E(
and not
to the opening angle of the jet. This interpretation means that
the GRB beams are wide and hence the rate of GRBs is smaller than
the rate implied by the usual beaming factor. On the other hand it
implies that GRBs are more energetic.
Guetta et al.
[153]
estimate that this factor (the
ratio of the fixed energy of a "structured" jet relative to the
energy of a uniform jet to be ~ 7. However they find that the
observing angle distribution is somewhat inconsistent with the
simple geometric one that should arise in universal structured
jets (see also Nakar et al.
[266],
Perna et al.
[299]).
The energy-angle relation discussed earlier require (see
Section VIII below) an angle dependent jet
with E( )
)

 -2.
-2.
Regardless of the nature of the jet (universal structured jet or uniform with a opening angle that differs from one burst to another) at late time it becomes non relativistic and spherical. With no relativistic beaming every observer detects emission from the whole shell. Radio observations at this stage enable us to obtain a direct calorimetric estimate of the total kinetic energy of the ejecta at late times [107] Estimates performed in several cases yield a comparable value for the total energy.
If GRBs are beamed we should expect orphan afterglows (see Section VIIK): events in which we will miss the GRB but we will observe the late afterglow that is not so beamed. A comparison of the rate of orphan afterglows to GRBs will give us a direct estimate of the beaming of GRBs (and hence of their energy). Unfortunately there are not even good upper limits on the rate of orphan afterglows. Veerswijk [421] consider the observations within the Faint Sky Variability Survey (FSVS) carried out on the Wide Field Camerea on teh 2.5-m Isacc Newton Telescope on La Palma. This survey mapped 23 suare degree down to a limiting magnitude of about V = 24. They have found one object which faded and was not detected after a year. However, its colors suggest that it was a supernova and not a GRB. Similarly, Vanden Berk et al. [420] find a single candidate within the Sloan Digital Sky Survey. Here the colors were compatible with an afterglow. However, later it was revealed that this was a variable AGN and not an orphan afterglow. As I discuss later this limits are still far to constrain the current beaming estimates (see Section VIIK).
One exception is for late radio emission for which there are some
limits [215,
298].
Levinson et al.
[215]
show that the number of orphan radio
afterglows associated with GRBs that should be detected by a
flux-limited radio survey is smaller for a smaller jet opening
angle  . This might seen
at first sight contrary to
expectation as narrower beams imply more GRBs. But, on the other
hand, with narrower beams each GRB has a lower energy and hence
its radio afterglow is more difficult to detect. Overall the
second factor wins. Using the results of FIRST and NVSS surveys
they find nine afterglow candidates. If all candidates are
associated with GRBs then there is a lower limit on the beaming
factor of f-1b
. This might seen
at first sight contrary to
expectation as narrower beams imply more GRBs. But, on the other
hand, with narrower beams each GRB has a lower energy and hence
its radio afterglow is more difficult to detect. Overall the
second factor wins. Using the results of FIRST and NVSS surveys
they find nine afterglow candidates. If all candidates are
associated with GRBs then there is a lower limit on the beaming
factor of f-1b
 (
( 2 / 2) >
13. If none are associated with GRBs they find
f-1b > 90. This give
immediately a corresponding upper limit on the average energies of
GRBs. Guetta et al.
[153]
revise this values in view of a recent estimates of the correction to
the rate of GRBs to: f-1b = 40.
2 / 2) >
13. If none are associated with GRBs they find
f-1b > 90. This give
immediately a corresponding upper limit on the average energies of
GRBs. Guetta et al.
[153]
revise this values in view of a recent estimates of the correction to
the rate of GRBs to: f-1b = 40.
When considering the energy of GRBs one has to remember the
possibility, as some models suggest, that an additional energy is
emitted which is not involved in the GRB itself or in the
afterglow. van Putten and Levinson
[418],
for example, suggest
that a powerful Newtonian wind collimates the less powerful
relativistic one. The "standard jet" model also suggests a large
amount of energy emitted sideways with a lower energy per solid
angle and a lower Lorentz factors. It is interesting to note that the
calorimetric estimates mentioned earlier limit the total amount of
energy ejected regardless of the nature of the flow. More
generally, typically during the afterglow matter moving with a
lower Lorentz factor emits lower frequencies. Hence by comparing
the relative beaming of afterglow emission in different wavelength
one can estimate the relative beaming factors,
f-1b(E), at
different wavelength and hence at different energies.
Nakar and Piran
[272]
use various X-ray searches for orphan X-ray
afterglow to limit the (hard) X-ray energy to be at most comparable
to the  -rays
energy. This implies that the total energy of matter
moving at a Lorentz factor of ~ 40 is at most comparable to
the energy of matter moving with a Lorentz factor of a few hundred
and producing the GRB itself. At present limits on optical orphan
afterglow are insufficient to set significant limits on matter
moving at slower rate, while as mentioned earlier radio
observations already limit the overall energy output.
-rays
energy. This implies that the total energy of matter
moving at a Lorentz factor of ~ 40 is at most comparable to
the energy of matter moving with a Lorentz factor of a few hundred
and producing the GRB itself. At present limits on optical orphan
afterglow are insufficient to set significant limits on matter
moving at slower rate, while as mentioned earlier radio
observations already limit the overall energy output.
These observations won't limit, of course, the energy emitted in gravitational radiation, neutrinos, Cosmic Rays or very high energy photons that may be emitted simultaneously by the source and influence the source'e energy budget without influencing the afterglow.