


Techniques for inferring an IMF for a galaxy, as opposed to a star cluster or stellar population, date back to early population synthesis work in the 1960s (Spinrad, 1962, Wood, 1966, Spinrad, 1966, Spinrad & Taylor, 1971) that claimed an excess of M dwarfs in the nuclei of nearby galaxies. Wood (1966) also claim a proportionally larger number of giants for the spiral arms of NGC 224, NGC 3031 (M81), and NGC 5194, “essentially identical with that for the Solar neighbourhood.” This approach synthesised galaxy spectra by combining stellar spectra to reproduced the observed galaxy colours and certain spectral features including Mg b and Na D, as well as molecular bands including TiO and CN. These early analyses were focused largely on understanding the stellar populations and explaining the mass-to-light ratio for these systems, rather than constraining the IMF explicitly. Subsequently, Whitford (1977) showed that the Wing-Ford band was also a sensitive probe of the dwarf-to-giant ratio, and demonstrated that it could be used to constrain the IMF for old stellar populations within galaxies. This approach has been revived (e.g., van Dokkum & Conroy, 2012) and is now used routinely to infer IMF properties for early-type galaxies.
A different kind of approach was used by Kennicutt (1983), who introduced a diagnostic comparing the equivalent width of Hα (sensitive to the presence of high mass stars) to an optical colour index (sensitive to low mass stars), as a probe of the IMF. Using this approach, Kennicutt et al. (1994) showed that the high mass slope of the IMF in nearby spiral galaxies is flatter (−2.5 ≲ αh ≲ −2.35) than the Solar neighbourhood IMF of Miller & Scalo (1979) or Scalo (1986) (−3.3 ≲ αh ≲ −2.7). They attribute this at least in part to a deficiency of high mass stars in the small volume of the Galaxy used to construct the local IMF, noting that Parker & Garmany (1993) find flatter slopes for the high mass end of the IMF in 30 Dor in the LMC.
Yet another approach is the Hα-to-UV flux ratio, originally proposed by Buat et al. (1987) as an IMF probe. They used a sample of 31 late type galaxies to find a high mass (m > 1.8 M⊙) IMF slope ranging over −3.1 < αh < −2.3. They note that the dispersion in slope is smaller, ± 0.25, for the sub-sample of 17 galaxies most similar to the Milky Way. Other approaches, including UV luminosities and mass-to-light ratio techniques, have been summarised by Scalo (1986) and Kennicutt (1998). Subsequently many of these approaches have been refined and used extensively. More recent approaches include the IGIMF approach of Kroupa & Weidner (2003), which has been explored extensively over the past decade (e.g., Yan et al., 2017).
Different kinds of integrated galaxy techniques have been used for different kinds of galaxies. The Kennicutt (1983) and Buat et al. (1987) diagnostics, and the use of UV luminosities directly as an IMF probe have focused on currently star forming galaxies, while the mass-to-light ratio and dwarf-to-giant ratio approaches have focused on passive galaxies. This is natural given the requirements or limitations of each technique, but it causes difficulty in directly comparing the results between the approaches. For now I summarise the various methods based on the galaxy type they are used to probe, and explore the comparisons between them further below in § 5.4 and § 9.
The IMF for galaxies with active star formation, even at a low level, is able to be probed with diagnostics relying on emission associated with young high mass stars. The early work by Kennicutt (1983) and Kennicutt et al. (1994) was extended by Hoversten & Glazebrook (2008) using data from the Sloan Digital Sky Survey DR4 (Adelman-McCarthy et al., 2006). They concluded that the sample as a whole was best fit by an IMF with high mass (m > 0.5 M⊙) slope αh = −2.45 with negligible random error and systematic error of ± 0.1. While noting that a constraint on αh is degenerate with one on mu, they also showed that brighter galaxies are better fit with a slightly flatter slope of αh ≈ −2.4, and that fainter galaxies are not well described by a “universal” IMF, inferring fewer massive stars leading either to steeper αh or lower mu. They point out that stochastic SFHs may mimic or contribute to this kind of signature, although by testing models for such stochastic SFHs they conclude that to reproduce the measurements for the observed population of bright galaxies would require an “implausible coordination of burst times”.
The same method was used by Gunawardhana et al. (2011) with data from the Galaxy And Mass Assembly survey (Driver et al., 2011, Hopkins et al., 2013, Liske et al., 2015). Using three independent volume-limited galaxy samples spanning 0.1 ≲ z ≲ 0.35, they find a trend between the high mass (m > 0.5 M⊙) IMF slope and SFR (Figure 3) or SFR surface density (ΣSFR). With the large sample available they are able to explore in detail the dependency of αh on these properties, which they quantify through the relations αh ≈ 0.36 log(SFR / M⊙ yr−1) − 2.6 or αh ≈ 0.3 log(ΣSFR / M⊙ yr−1 kpc−2) − 1.7. For the range of SFR or ΣSFR they probed, this leads to a variation in the high mass IMF slope from αh ≈ −2.5 for the least active star forming systems (SFR ≈ 0.1 M⊙ yr−1) to αh ≈ −1.7 for the most active (SFR ≈ 50 M⊙ yr−1). They point out that for the current SFR of the Milky Way, these results would imply a value of αh ≈ −2.35, which is an encouraging consistency check. They also comment that the SFR dependence would imply a flatter high mass IMF slope (αh > −2.35) in the Milky Way's early history, given that it had an elevated SFR in the past.
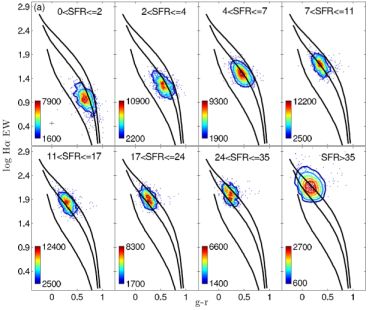 |
Figure 3. Following Kennicutt (1983) and Hoversten & Glazebrook (2008), this diagnostic shows how IMFs with different αh can be discriminated using the equivalent width of Hα and an optical colour, in this case (g − r). The solid tracks are the evolutionary paths followed through a star formation event, showing (top to bottom) the location expected for αh = −2, αh = −2.35, αh = −3. The data correspond to galaxies in the highest redshift bin of the three volume limited samples, with ⟨ z ⟩ = 0.29, split into eight bins of SFR. This illustrates the tendency for the higher SFR systems to favour IMFs with flatter high mass slopes (more positive αh). See Gunawardhana et al. (2011) for details. Reproduced from Figure 6a of “Galaxy and Mass Assembly (GAMA): the star formation rate dependence of the stellar initial mass function,” Gunawardhana et al. (2011). |
Gunawardhana et al. (2011) note that while the SFR is an IMF-dependent quantity, applying an IMF-dependent SFR calibration would not qualitatively alter their conclusions, since the variation seen is monotonic, and would only have the effect of reducing the range of SFR sampled. Gunawardhana et al. (2011) also explore degeneracies in the variation of the IMF that would lead to the same observed combination of Hα equivalent width and g − r colour. They show that while the high mass slope can be fixed at the Salpeter value (αh = −2.35) and the results explained by allowing mc to increase, it requires a very high value of mc ≈ 10 M⊙ to account for the highest star forming systems, reminiscent of the early results for starburst nuclei (Rieke et al., 1980) that are no longer favoured (Elmegreen, 2007).
Again to rule out the possibility that stochastic SFHs could be the origin of the observed signature, Gunawardhana et al. (2011) extended the analysis of Hoversten & Glazebrook (2008) by demonstrating that both stellar mass and mass-doubling time for the observed galaxies vary smoothly along the SPS model tracks. They found no signature corresponding to the significant bursts of star formation that would be seen if stochastic SFHs were the dominant effect. Subsequently, Nanayakkara et al. (2017), too, demonstrated quantitatively that stochastic star formation histories could not explain their measurements, in a sample at much higher redshift. Gunawardhana et al. (2011) further demonstrate that the result is robust to the implementation of dust correction and choice of population synthesis model. While there is a degeneracy between a varying high mass αh and a varying mc, it is possible to exclude a variation in ml (Figure 4). It is clear that a varying low mass cutoff has a very different signature in this diagnostic than a varying high mass slope or mc. This confirms that the results of Gunawardhana et al. (2011) are not attributable to variations in ml while maintaining a Salpeter value for the high mass slope.
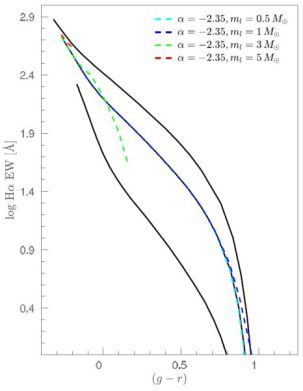 |
Figure 4. The IMF diagnostic used by Gunawardhana et al. (2011) to identify variations in the slope of the high mass (m > 0.5 M⊙) IMF. The black solid lines show the evolutionary tracks expected for galaxies with, from top to bottom, αh = −2, −2.35, −3. The additional tracks (dashed coloured lines) illustrate the effect of a fixed high mass slope (α = −2.35) but varying ml. The tracks become shorter as ml increases, due to the shorter lifetimes of the higher mass stars. Figure courtesy of M. Gunawardhana. |
These results were extended to z ≈ 2 by Nanayakkara et al. (2017), finding that systems with the highest Hα equivalent widths could only be explained either by rotating extremely metal poor stars with binary interactions, or IMFs with αh > −2 (0.5 < m / M⊙ < 120). They note that in the latter case, no single IMF slope could reproduce the data, implying a need for a stochastically varying high mass IMF slope. They explore the trend with SFR derived from Hα and from the combined UV and far-infrared (FIR) luminosities, finding a weak trend with the Hα SFR in the same sense as that of Gunawardhana et al. (2011), but none with the SFRs from the UV+FIR (their Figure 21). This arises from the lowest Hα SFR systems having higher SFRs as measured by the UV+FIR. In order to avoid internal inconsistencies, it would be valuable for all analyses of this kind to present results in terms of IMF-independent quantities (such as luminosities) or to calculate SFRs or other IMF-dependent properties self-consistently assuming whatever IMF-dependency on αh or other parameter is being tested.
At similar redshifts, Zhang et al. (2018) measure the 13C / 18O abundance ratio, probed through the rotational transitions of the 13CO and C18O isotopologues, for four starburst galaxies. These galaxies are gravitationally lensed submillimetre galaxies spanning 2.3 < z < 3.1. They find low ratios compared to chemical evolutionary models for the Milky Way, implying considerably more high mass stars in such starbursts than in typical spiral galaxies, and with a high mass slope flatter than that of Kroupa (2001).
At the opposite end of the scale, the Buat et al. (1987) approach relying on Hα-to-UV flux ratios has more recently been used to focus on potential variations to the IMF for low mass or low SFR galaxies. The results of Meurer et al. (2009), Lee et al. (2009), and Boselli et al. (2009) all suggest that for low SFR (or low luminosity, or low mass) galaxies, there is evidence of a deficiency of high mass stars, characterised as an IMF slope steeper than Salpeter (α < −2.35 for 0.1 < m / M⊙ < 100). As the Hα luminosity (or surface density) decreases within various samples of nearby galaxies, these authors show that the Hα luminosity (or flux) declines faster than that of the UV. This is in the opposite sense than could be explained through dust obscuration, which affects the UV proportionally more than Hα, although different levels of attenuation for the line and continuum emission may play some role (e.g., Charlot & Fall, 2000). Pflamm-Altenburg et al. (2009) demonstrate how this result can arise within the IGIMF formalism.
After exploring and ruling out a range of possible scenarios, including dust obscuration, SFH, stochastic population of the IMF, metallicity, and escape fraction, Meurer et al. (2009) conclude that the most likely scenario is a variation in the high mass end of the IMF, with either mu ranging over 30 ≲ mu / M⊙ ≲ 120 or having a varying IMF slope spanning −3.3 ≲ α ≲ −1.3 (for 0.1 < m / M⊙ < 100), in the sense that the lower SFR systems have either lower mu or steeper α. It is worth noting the use of the single power law IMF slope extending to the lowest masses here, and questioning whether a slope change below some mc would affect the results. Since the diagnostic uses flux ratios of indicators sensitive only to high mass stars, though, it seems unlikely that changing this assumption would alter the IMF conclusions significantly.
The results of Meurer et al. (2009) are qualitatively similar to those of Gunawardhana et al. (2011), with a high mass IMF slope that gets progressively steeper as ΣSFR becomes lower. Quantitatively, though, the results are somewhat different, with Meurer et al. (2009) inferring steeper IMF slopes at a given value of ΣSFR (or equivalently, ΣHα) than Gunawardhana et al. (2011), when retaining the same mu. Specifically, as an example, at log(ΣSFR / M⊙ yr−1 kpc−2) = −2.7 Gunawardhana et al. (2011) find αh ≈ −2.4 (their Figure 13c). This value of ΣSFR corresponds to log(ΣHα / W kpc−2) = 31.4, for which Meurer et al. (2009) find a typical value of log((FHα / fFUV) / Å) ≈ 0.65 (their Figure 3), and which leads to αh ≈ −3.0 (their Figure 10b). I return to exploring the details of these quantitative differences below.
Again in a qualitatively similar fashion, Boselli et al. (2009) find that the IMF slope (for 0.1 < m / M⊙ < 100)spans −2.6 ≲ α ≲ −2.3, with steeper slopes for the lower mass galaxies. Comparing quantitatively to Gunawardhana et al. (2011), these slopes are closer than inferred by Meurer et al. (2009) but still rather steeper for a given stellar mass or sSFR. Based on Figure 10 of Boselli et al. (2009), α = −2.5 is favoured for galaxies with 9.2 < log(M / M⊙) < 9.8, for example. This corresponds broadly to a range of −10 ≲ log(sSFR / yr−1) ≲ −9 (see Figure 4 of Bauer et al., 2013) for the GAMA sample in the redshift range analysed by Gunawardhana et al. (2011). For this range of sSFR, Gunawardhana et al. (2011) find high mass IMF slopes spanning −2.4 ≲ αh ≲ −2.1 (their Figure 13b), somewhat flatter than the α = −2.5 of Boselli et al. (2009).
Boselli et al. (2009) invoke bursty SFHs to explain their findings in preference to IMF variations, contradicting the claim by Meurer et al. (2009) that the “gasps” between such bursts would have to be unrealistically synchronised between galaxies to produce the range of measured flux ratios. Boselli et al. (2009) note that the star formation in dwarf galaxies can be dominated by a single Hii region, which can lead to larger scatter in the Hα to UV flux ratio than for high mass galaxies, arising from the different lifetimes of the OB stars (∼ 106 yr) responsible for the Hα emission and the A stars (∼ 107 yr) responsible for the UV emission.
Lee et al. (2009) use a nearby sample of galaxies to probe to extremely low levels of SFR, down to SFR ≈ 10−4 M⊙ yr−1, and see very similar effects to the results of Meurer et al. (2009) and Boselli et al. (2009). They do not attempt to constrain the IMF directly but instead test (and rule out) a variety of explanations, while noting that the IGIMF predictions of Pflamm-Altenburg et al. (2009) match their observations surprisingly well, before also implying a preference for SFH variations (bursty or “flickering”) as a possible explanation (see also Lee et al., 2011). In contrast, Fumagalli et al. (2011) argue, based on a stochastic code for synthetic photometry, that these observed Hα-to-UV flux ratios in low SFR galaxies can be explained by random sampling from a “universal” IMF, combined with stellar evolution. A similar result was found by Weisz et al. (2012) who note that such stochastic SFHs can explain the observed Hα to UV flux ratios in low mass galaxies, without invoking IMF variations.
Bearing in mind the likely contributions of stochastic SFHs, there does seem to be some evidence for the idea that systems with lower luminosities, masses or SFRs favour IMFs lacking in high mass stars relative to a Kroupa (2001) or Chabrier (2003a) IMF. This is reinforced by studies of the LMC, SMC, and other dwarf, low metallicity, or low surface brightness galaxies. Using UV imaging of the LMC and models jointly constraining IMF slope, obscuration and age, Parker et al. (1998) find αh = −2.80 ± 0.09 (for m ≳ 7 M⊙). Lamb et al. (2013) find αh = −3.3 ± 0.4 (for m > 20 M⊙) in the SMC based on spectra for a spatially complete census of field OB stars. The dwarf starburst galaxy NGC 4214 was found by Úbeda et al. (2007) to have αh < −2.83 ± 0.07 (for 20 < m / M⊙ < 100), the upper limit arising due to the presence of unresolved binaries, the neglect of which acts to flatten the inferred IMF. Lee et al. (2004) use the high M/L ratios for seven low surface brightness disk galaxies to estimate α = −3.85 (for 0.1 < m / M⊙ < 60). Garcia et al. (2017) summarise studies of high mass stars in Local Group dwarf galaxies with very low metallicity, oxygen abundances less than 1/7 of the solar value. Although relying on a sample of only four galaxies, with incomplete observations of the high mass stellar population, they note that the highest mass stars so far identified have initial masses of m ≈ 60 M⊙. Bruzzese et al. (2015) explore the IMF of the dark-matter dominated, extremely low SFR, blue compact dwarf galaxy NGC 2915, and reinforce the possibility of high mass IMF slopes rather steeper than Salpeter for such systems. They combine colour magnitude diagrams for the stellar populations with an assumed recent SFH to find a high mass IMF slope αh = −2.85 (for m ≳ 4 M⊙) and a poorly constrained upper mass limit of mu = 60 M⊙. Noting the impact of assuming a constant recent SFH (Elmegreen & Scalo, 2006), the IMF may not be quite this extreme, although it is not inconsistent with the other results highlighted here, in similar environments. The same approach, assuming a constant star formation rate over the dynamical timescale, was used in inferring the IMF of the dwarf irregular galaxy DDO 154 by Watts et al. (2018), to derive αh = −2.45 with a similarly poorly constrained mu = 16 M⊙.
For the population of ultra-compact dwarf galaxies (UCDs), known to have high V-band mass-to-light ratios (ΥV), Dabringhausen et al. (2009) use population synthesis modelling to infer αh, after arguing that the non-baryonic dark matter contribution is too low to influence the dynamics of these systems (Murray, 2009). Contrary to the results above for other dwarf galaxy systems, they show that an IMF with a relative excess of high mass stars, αh ≈ −1.6 to αh ≈ −1.0 (depending on the assumed age), is required to account for the observed ΥV. This perhaps highlights star formation rate density as a significant factor in shaping the IMF. In contrast to the local dwarf systems, which are typically low surface density galaxies, the UCDs are expected to have formed rapidly, with SFRs as high as perhaps 10−100 M⊙ yr−1, and a correspondingly high ΣSFR given their small physical sizes. For a physical scale of 10 pc this would give 5 ≲ log(ΣSFR / M⊙ yr−1 kpc−2) ≲ 6, substantially higher than in the population of higher mass galaxies discussed above. The elevated values of αh inferred are qualitatively consistent with the results for higher mass star forming galaxies, although any potential dependence of αh on ΣSFR is quantitatively inconsistent with the nominal linear relations of Meurer et al. (2009), Gunawardhana et al. (2011) or Nanayakkara et al. (2017).
Using UV spectral lines as a constraint, Leitherer (2011) combines measurements for a sample of 28 nearby galaxies (distances less than 250 Mpc) to construct the average UV spectrum, and concludes that the high mass (m > 0.5 M⊙) IMF slope is constrained to lie between −2.6 ≲ αh ≲ −2.0. This range encompasses most of the variation in αh inferred from the studies described above, and consequently does not substantially rule out the proposed variations.
With the exception of the dwarf galaxies and low surface brightness galaxies, which show rather steeper high mass (m > 0.5 M⊙) IMF slopes (although noting the opposite result for UCDs, which are perhaps more analogous to starburst systems), the range spanned by αh from these investigations is not large, with most galaxies having −2.5 ≲ αh ≲ −1.8 (e.g., Gunawardhana et al., 2011), similar to the range seen in nearby stellar populations and star clusters, and variously attributed to observational or astrophysical limitations. It is notable that Gunawardhana et al. (2011) place the Milky Way on their relationship between α and SFR or ΣSFR, finding a Salpeter IMF slope (αh = −2.35) consistent with the bulk of analyses of Galactic stellar populations.
In summary, the observations for star forming galaxies suggest a broadly consistent picture in favour of IMF variations, with αh larger (flatter) for higher SFR or ΣSFR, and smaller (steeper) for lower SFR or ΣSFR. This is in line, qualitatively at least, with the results seen above for starburst or super star clusters.
The descriptor “passive” is intended here to refer to the degree of star formation, or rather its absence at any significant level, and is independent of the existence or not of an active galactic nucleus (AGN). The methods of Kennicutt (1983) and Buat et al. (1987) are not typically able to be applied to passive galaxies, as they have little or no Hα and UV emission arising from high mass young stars. Where such emission is present it is likely to arise from, and be dominated by, an AGN rather than star formation. Also, since the stars being probed in these passive galaxies are only those low mass objects remaining from star formation episodes much earlier, any IMF measured in such systems is in a sense a “relic” IMF, analogous to the PDMF in Milky Way stellar systems, and in many cases this has led naturally to a focus on the low mass end of the IMF.
A novel approach was explored by van Dokkum (2008), noting the opposing effect of the IMF on luminosity and colour evolution identified by Tinsley (1980), such that an IMF with proportionally more high mass stars would lead to stronger luminosity evolution and weaker color evolution. He compared the rate of luminosity and colour evolution for high mass elliptical galaxies in clusters spanning 0≤ z ≤ 0.83, and found a need for an IMF with α = −0.7−0.4+0.7 at masses around m ≈ 1 M⊙, much flatter than a Kroupa (2001) or Chabrier (2003a) IMF at these masses, to explain the observations. Casting this as an estimate of mc = 1.9−1.2+9.3 M⊙ at z = 3.7−0.8+2.3 (the estimated formation redshift of stars at this stellar mass) for a Chabrier-like IMF, and comparing with the lower inferred values of mc at lower redshift, he goes on to explore the impact of an evolving mc. He notes the effect of reducing the apparent discrepancy between the cosmic SFH and stellar mass density, confirming similar results (Hopkins & Beacom, 2006, Fardal et al., 2007, Wilkins et al., 2008a), and which I discuss in detail below in § 6. The result of van Dokkum (2008) was questioned by van Dokkum & Conroy (2012) who show instead that when comparing galaxies at a given velocity dispersion, rather than stellar mass, the observed luminosity and colour evolution is consistent with the standard Salpeter slope.
More recent approaches have focused on using spectral signatures sensitive to the dwarf-to-giant ratio, stellar mass-to-light ratios and kinematics to explore the inferred IMF.
The dwarf-to-giant ratio approach evolved from early work using Na i D lines as a tracer of dwarf star populations (Spinrad, 1962) which concluded that the most luminous and high mass elliptical galaxies showed evidence for proportionally more dwarf stars than found in lower mass galaxies. Additional spectral features (Mg i, Ca i, Ca ii, TiO, CN, CH, CaH, MgH) sensitive to different stellar populations (Spinrad, 1966, Wood, 1966, Spinrad & Taylor, 1971) enabled improvement of the ability to characterise the stellar populations present in integrated galaxy spectra. Whitford (1977) incorporated measurements of the Wing-Ford molecular band at 9910 Å to argue against the earlier results that favoured an excess of dwarf stars in such galaxies, ruling out IMFs with α ≤ −3, and finding results supporting an IMF with α ≈ −2.
This general technique has been developed significantly through recent work (e.g., van Dokkum & Conroy, 2010, van Dokkum & Conroy, 2012) and is illustrated by Figure 5, which has been reproduced from van Dokkum & Conroy (2012). A key result was that of van Dokkum & Conroy (2010), who apply the high resolution SPS models of Conroy et al. (2009) to estimate the proportion of low mass dwarf stars (m < 0.3 M⊙) necessary to explain the observed absorption in the Naiλλ 8183,8185Å doublet and the Wing-Ford FeH band around λ 9916Å for eight nearby elliptical galaxies in the Virgo and Coma clusters. They infer αl ≈ −3 for the low mass range (0.1 < m / M⊙ < 0.3), significantly steeper than the Salpeter slope. As these stars would have formed at high redshift (z = 2 − 5), they argue against high redshift IMFs with a deficit of low mass stars such as the truncated IMF of Baugh et al. (2005). Recall that for the Milky Way −1.4 ≲ αl ≲ −0.6 from the compilation of Bastian et al. (2010). van Dokkum & Conroy (2012) and Conroy & van Dokkum (2012) extended this result to the bulge of M31 and 34 galaxies from the SAURON integral field spectroscopy sample (Bacon et al., 2001), adding the Caii λλ 8498,8542,8662Å triplet to the diagnostics, and concluding that the low mass m < 0.3 M⊙ IMF slope varies systematically with galaxy velocity dispersion and α-enhancement, with steeper slopes in more massive and high-abundance galaxies (Figure 5).
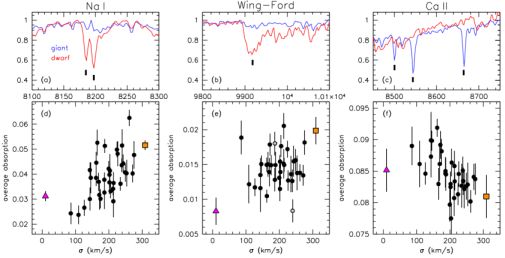 |
Figure 5. Three spectral regions showing features sensitive to the presence or absense of low mass stars (upper panels), and the trend in the absorption strength of those feature seen with velocity dispersion of the galaxies (lower panels). This demonstrates that galaxies with higher velocity dispersion, and hence higher stellar mass, have a tendency to favour an excess of dwarf, or low mass, stars. See van Dokkum & Conroy (2012) for details. (Figure 10 of “The stellar initial mass function in early-type galaxies from absorption line spectroscopy. I. Data and empirical trends,” van Dokkum & Conroy (2012), © AAS. Reproduced with permission.) |
Using similar approaches, both Spiniello et al. (2012) and Ferreras et al. (2013) infer IMF slopes for the same mass range steeper than Salpeter (αl ≈ −3) for high velocity dispersion systems (σ ≳ 300 km s−1), and La Barbera et al. (2013) also find IMF slopes steeper than Salpeter for systems with σ ≳ 220 km s−1. Zaritsky et al. (2014a) find a strong correlation between UV colour and Υ* for the same sample of galaxies analysed by van Dokkum & Conroy (2012), and conclude that this correlation is attributable to varying populations of extreme horizontal branch stars arising from the IMF variations.
For lower stellar mass systems, Smith et al. (2012) analysed 92 red-sequence galaxies in the Coma cluster, including more galaxies with lower velocity dispersions than van Dokkum & Conroy (2012) and Conroy & van Dokkum (2012). They found no clear dependence of IMF slope on velocity dispersion with a Salpeter slope adequate for 100 ≲ σ / km s−1 ≲ 250 (although they do not rule out steeper IMF slopes at higher velocity dispersions), but they do see a dependence on α-enhancement (Mg/Fe ratio), concluding that the IMF variation arises as a result of star formation mode, with rapid bursts leading to proportionally more low-mass stars (m < 0.3 M⊙).
In parallel with these analyses, gravitational lensing and dynamical constraints were being explored as a tool for inferring mass-to-light ratios (Υ) and placing associated constraints on IMF slopes. This approach was refined by Treu et al. (2010) who infer Υ for 56 galaxies from the SLACS survey (Bolton et al., 2006). They introduce an IMF mismatch parameter, also denoted α, which is defined to be the ratio of Υ inferred independently from the lensing and dynamical analysis compared to that from SPS modelling. For clarity, I refer to the IMF mismatch parameter as αmm = ΥLD / ΥSPS throughout.
Treu et al. (2010) find that, with the assumption of an NFW dark matter profile (Navarro et al., 1996), such galaxies tend to favour IMFs such as Salpeter that provide a higher Υ* than those of Chabrier (2003a). While stellar mass range is not discussed, the Bruzual & Charlot (2003) models used span a mass range of 0.1 ≤ m / M⊙ ≤ 100, and from the scale of the IMF mismatch parameter it is reasonable to infer that the Salpeter IMF slope (α = −2.35) is applied over that full range for their Salpeter SPS mass estimates (confirmed by T. Treu, personal communication). Treu et al. (2010) also note that their sample is limited to relatively high velocity dispersion systems, and show that, while for galaxies with σ≈ 200 km s−1 a Chabrier (2003a) IMF provides consistent Υ* with the lensing and dynamical estimate, “heavier” IMFs (i.e., with a greater total mass normalisation) are required for higher velocity dispersion systems. They conclude that either the IMF varies toward one with a Salpeter-like mass normalisation for the most massive galaxies, or that dark matter profiles are not universal and the inner slope is systematically steeper than NFW for the most massive galaxies, or possibly a combination of both. This result is still not as extreme as the αl ≈ −3 found spectroscopically by van Dokkum & Conroy (2010).
Similarly, Läsker et al. (2013) use a combination of dynamical models and the SPS and IMF approach of Vazdekis et al. (1996), Vazdekis et al. (2012) to infer an IMF with a steep high mass slope, (αh = −4.2 ± 0.1 for m > 0.6 M⊙ constraining αl = −1.3 for 0.1 < m / M⊙ < 0.6) in a low redshift (z = 0.116) high mass (σ = 360 km s−1) early type galaxy with a putative extremely high mass nuclear black hole. In apparent contrast to these results, though, Smith & Lucey (2013) used gravitational lensing mass estimates to demonstrate that Υ* for a high mass (σ≈ 330 km s−1) low-redshift (z = 0.035) giant elliptical is consistent with a Kroupa (2001) IMF. This result was subsequently reinforced by Smith et al. (2015a) who analysed three high mass (σ > 300 km s−1) low redshift (z ≲ 0.05) galaxies, showing that the inferred IMF mass normalisation is consistent with that of Kroupa (2001), and excluding a Salpeter IMF (α = −2.35 over 0.1 < m / M⊙ < 100) at the 3.5 σ level.
These results, though, are not inconsistent with the scatter seen by Treu et al. (2010) in their IMF mismatch parameter. It is worth reiterating that Treu et al. (2010) use the observed small range of scatter on αmm to argue that “the absolute normalization of the IMF is uniform to better than 25%”, a result that echoes the relatively small range of potential variations found for the star forming galaxy population, although with a different sense in the variation itself for the passive galaxies (i.e., higher mass passive galaxies favouring proportionally more low mass stars, but higher mass star forming galaxies favouring proportionally more high mass stars).
There is a subtlety around gas recycling in SPS that affects the M/L ratio comparison technique. Whether the gas recycled through stellar evolution is retained or not in the SPS inferred masses has a direct impact on the comparison to masses inferred from lensing and dynamics. Treu et al. (2010) explore the two extreme cases, where all gas lost through stellar evolution is removed, and where it is retained (the “zero age” SPS mass). They note that for a Chabrier (2003a) IMF the “zero age” masses tend to be overestimates compared to the lensing masses, implying that at least some fraction of the gas associated with recycling is expelled and does not contribute to the baryonic mass in the region probed by the lensing and dynamical constraints. In this and subsequent work, it is typically just the mass in stars and stellar remnants derived from the SPS that is compared with the lensing and dynamical mass estimates, which for early type galaxies with very low gas fractions is likely to be a reasonable assumption. It must be noted, though, that such mass estimates may be lower limits if some gas component still contributes non-negligibly to the baryonic mass, and needs to be accounted for in the uncertainties on inferred IMF constraints.
Another significant development around the same time was the use of stellar kinematics and dynamical models to constrain the IMF (Cappellari et al., 2012, Cappellari et al., 2013) They used the ATLAS3D sample of 260 early-type galaxies (Cappellari et al., 2011) combining the measured stellar kinematics with detailed axisymmetric dynamical models, to derive accurate stellar masses and mass-to-light ratios for the population. By comparing the mass-to-light ratio measured dynamically in this way to that inferred from the photometry using SPS models that assume a Salpeter IMF over the full mass range (0.1 < m / M⊙ < 100), they are able to show a systematic variation in the inferred IMF normalisation. This variation ranges from a mass normalisation consistent with Chabrier (2003a) or Kroupa (2001) at Υ* ≈ 2 M⊙ / L⊙ to one consistent with a Salpeter slope spanning 0.1 ≤ m / M⊙ ≤ 100 at Υ* ≈ 6 M⊙ / L⊙ (Figure 6). This may extend to even higher mass normalisations at the most extreme measured values of Υ* ≈ 10 M⊙ / L⊙, with an IMF characterised equally by α = −2.8 (dominated by low mass stars) or α = −1.5 (dominated by high mass stars). This result has been questioned by Clauwens et al. (2015), though, who note that these trends could also be produced if the kinematic mass estimates had Gaussian errors of the order of 30%.
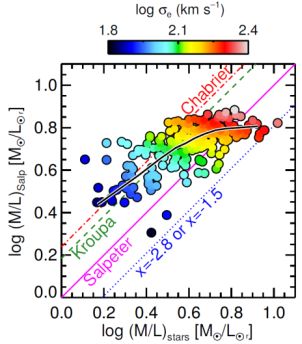 |
Figure 6. The mass-to-light ratio for the stellar component of ATLAS3D galaxies estimated using dynamical models, (M/L)stars, compared to that estimated from spectral fitting using SPS models assuming a fixed Salpeter IMF, (M / L)Salp. This demonstrates the trend for the high mass-to-light, or high velocity dispersion, galaxies in this sample to favour IMFs with an excess of mass compared to the IMFs of Chabrier (2003a) or Kroupa (2001), approaching and exceeding that from a Salpeter slope over the full mass range (an excess of low mass stars). See Cappellari et al. (2013) for details. Reproduced from Figure 11 of “The ATLAS3D project – XX. Mass-size and mass-σ distributions of early-type galaxies: bulge fraction drives kinematics, mass-to-light ratio, molecular gas fraction and stellar initial mass function,” Cappellari et al. (2013). |
There are significant degeneracies possible in IMF shape when only the mass normalisation is constrained. While this is highlighted for the very high mass normalisations by Cappellari et al. (2013), that of a Salpeter IMF slope (α = −2.35) over the full mass range can also be reproduced by an IMF with a Milky Way style low mass slope, and an excess of high mass stars. By way of illustration, this is achieved (including only the mass in stars and stellar remnants) by an IMF with αl = −1.5 (0.1 ≤ m / M⊙ ≤ 0.5) and αh = −1.70 (0.5 ≤ m / M⊙ ≤ 100), or an IMF with the Kroupa (2001) low mass slope αl = −1.3 (0.1≤ m / M⊙ ≤ 0.5) and αh = −1.64 (0.5 ≤ m / M⊙ ≤ 100). Different combinations can equally be used to match the zero-age mass normalisation. The point is that a value of Υ* consistent with a Salpeter IMF over the full mass range doesn’t necessarily imply an excess of low mass stars. To break this degeneracy, Conroy et al. (2013) quantitatively compared the scale of the IMF mass normalisation derived using the dwarf-to-giant approach with that from dynamical mass constraints, and find that they are consistent, inferring that the explanation lies in an excess of low mass stars (m ≲ 1 M⊙).
There have also been a range of enhancements and refinements that combine lensing, dynamical and SPS constraints. These results largely confirm the need for a low mass IMF slope similar to the Salpeter value for high mass early type galaxies. Spiniello et al. (2015a), for example, find a low mass slope of αl = −2.37 ± 0.12 and ml = 0.131−0.026+0.023 M⊙ at a reference point corresponding to σ = 250 km s−1 for 9 early type galaxies, confirming earlier results by Barnabè et al. (2013). In apparent contrast Lyubenova et al. (2016), using 27 early type galaxies from CALIFA (Walcher et al., 2014) and the IMF parameterisation approach of Vazdekis et al. (1996), rule out a single power-law IMF and conclude that a double power-law with a varying high-mass slope is required to explain the dynamical and stellar M/L ratios. This result may not be inconsistent with most of the results above, to the degree that it is only the mass normalisation that is being constrained through this approach, but it would be inconsistent with the conclusions of Conroy et al. (2013). Testing the consistency of IMF measurements between the SPS and the lensing and dynamical approaches is clearly important, and some work in this area has already begun (Newman et al., 2017). Using three strongly lensed passive galaxies, Newman et al. (2017) find consistent IMF estimates between the two techniques for one galaxy, but require a variable low-mass cutoff or a nonparametric form of the IMF to reconcile the approaches for the remaining two systems. Clearly, extending such analyses to larger samples is desirable.
More recently these approaches have been extended to identify radial gradients in the IMF shape (van Dokkum et al., 2017). They characterise their results using a variant of the αmm IMF mismatch parameter which, instead of comparing dynamical to SPS M/L ratios, compares the Υ* inferred from a given SPS fit to a canonical Milky Way IMF such as Kroupa (2001) or Chabrier (2003a) as a convenient shorthand for encapsulating the relative mass normalisation. Using αmm = ΥSPS / ΥMW in this way, they find IMFs with mass normalisations heavier than Kroupa (2001) or Chabrier (2003a) (αmm ≈ 2.5) in the central regions for six early type galaxies, but approaching the Milky Way value as radius increases, with αmm ≈ 1.1 at R > 0.4 Re. The SPS IMF constraint approach has also been refined by Conroy et al. (2017), who developed a non-parametric approach to constraining the m < 1 M⊙ shape. Applying this to the centre of NGC 1407, they find an IMF slope consistent with αl = −2.7. Such radial trends may provide an explanation for the differences found in the IMF properties between the spectroscopic and the dynamical approaches. It is also a tantalising link to the postulated “two-phase” formation scenario for early type galaxies (e.g., González Delgado et al., 2017), which proposes that the cores of elliptical galaxies formed quickly and quenched rapidly, (the high redshift “red nuggets”), in contrast to their outer regions. Martín-Navarro et al. (2015b) find a “bottom-heavy” IMF (1.5 ≲ αmm ≲ 2) out to 1.5 Re in NGC 1277, and argue that this is an example of the kind of “core” that would evolve through dry merging to the characteristic masses and sizes of z ≈ 0 elliptical systems.
Martín-Navarro et al. (2015d) argue that metallicity, rather than velocity dispersion, is the driver of IMF variations in early type galaxies, building on their earlier work (Martín-Navarro et al., 2015a, Martín-Navarro et al., 2015b) using the SPS and IMF parameterisation approach of Vazdekis et al. (1996). Using five key spectral features sensitive to metallicity, age and the IMF, they add a sample of 24 galaxies from CALIFA to the earlier work, jointly constraining the metallicity and high mass (m > 0.6 M⊙) IMF slope, with the low mass (m < 0.6 M⊙) slope fixed at the Kroupa (2001) value (αl = −1.3). They find a metallicity dependence on the high mass slope expressed as αh = −3.2(± 0.1) − 3.1(± 0.5)[M/H], consistent with a Kroupa (2001) high mass slope (αh = −2.3) for metallicities [M/H] ≈ −0.3, and steeper for higher metallicity. They also fit for a single power law, finding that the data could also be explained by an IMF with slope α = −2.5(± 0.05) − 2.1(± 0.2)[M/H] over the full mass range (0.1 ≤ m / M⊙ ≤ 100). They go on to demonstrate that the relationship observed by other authors between IMF slope and stellar velocity dispersion naturally arises, qualitatively at least, through a combination of the mass-metallicity relation (e.g., Tremonti et al., 2004, Lara-López et al., 2013) and their derived IMF slope relation with metallicity. Martín-Navarro et al. (2015d) further assert that the evolution in metallicity during galaxy formation implies an evolving IMF, drawing on arguments for IMFs dominated by high mass stars in low metallicity environments (Marks et al., 2012) transitioning to IMFs with a relative excess of low mass stars as the metallicity rapidly increases. They also point to similar arguments by Arrigoni et al. (2010) in favour of an evolving IMF for early type galaxies, based on chemical evolution in semi-analytic models. This conclusion contrasts with the analysis of 212 ATLAS3D early type galaxies by McDermid et al. (2014) who conclude that there are no strong trends between any of the stellar population derived parameters (age, metallicity, [α/Fe]) and the IMF mass normalisation.
More significantly, perhaps, Martín-Navarro (2016) show that, in order for passive galaxies to have both enhanced [Mg/Fe] ratios and an IMF overabundant in low mass stars relative to the Salpeter slope (αl < −2.35), they must have had extremely short star formation episodes that imply exceptionally high SFRs at high redshift, SFR ≈ 105 M⊙ yr−1, which have not been observed. They present two possible scenarios to resolve this issue. The first invokes an IMF overabundant in both low and high mass stars. The second argues for a time varying IMF, initially overabundant in high mass stars to account for the chemical signature, evolving to one overabundant in low mass stars at later times.
The results described above have generally used relatively low redshift galaxy samples. Exploring the higher-redshift Universe (0.9 < z < 1.5) Martín-Navarro et al. (2015c) use the TiO2 IMF-sensitive spectral feature and the Vazdekis et al. (1996) SPS and IMF parameterisation, finding αh = −4.2 ± 0.2 (for m > 0.6 M⊙) for the most massive galaxies (with stellar masses M* > 1011 M⊙), and slightly less steep (αh = −3.7−0.3+0.4) at lower stellar mass (2 × 1010 < M* / M⊙ < 1011). With estimated ages of 1.7 ± 0.3 Gyr, this population would have formed at redshifts of 1.5 ≲ z ≲ 3. These IMF slopes are similar to those found in the low redshift population for the highest metallicity galaxies by Martín-Navarro et al. (2015d), which have similar formation epochs (z ≈ 2) based on the ages inferred in that analysis.
Using a different approach again, Dabringhausen et al. (2012) measure the low mass X-ray binary (LMXB) population in globular clusters and UCDs within 11 elliptical galaxies of the Virgo Cluster. They conclude that these are 10 times more frequent in UCDs than expected from a Kroupa (2001) IMF, implying an excess of high mass stars. When the LMXB number is compared against an optical or infrared galaxy luminosity, this provides a direct constraint of the high mass end of the IMF (the progenitors of the neutron stars and black holes detected as LMXBs) compared to the low mass stellar population. In contrast, Peacock et al. (2014) find no evidence for IMF variations in a sample of 8 early type galaxies, based on their LMXB population. Their results are based on a small sample, and are consistent with the range of scatter seen by Treu et al. (2010). In either case, this demonstrates an important complementary approach to constraining the IMF. The presence of a low mass companion in an LMXB also implies a degree of binarity that is often neglected in common SPS models. There is clearly scope to expand this kind of analysis to larger samples and through incorporating such SPS models (e.g., Eldridge, 2012, Eldridge et al., 2017).
Other complementary approaches that have been recently explored for estimating integrated galaxy IMFs include the demonstration by Recchi et al. (2014) of how the plateau in the [α/Fe] ratio for a galaxy is sensitive to the galaxy IMF, and can be used as a test of whether IMFs vary between galaxies. Brewer et al. (2014) present a hierarchical modelling approach that can be used to derive upper limits on departures from universality in the IMF. Podorvanyuk et al. (2013) introduce a pixel-based SPS fitting approach, similar to the “pixel-z” technique (Conti et al., 2003, Welikala et al., 2008, Welikala et al., 2009) that fits pixel colours to infer stellar population ages, obscurations and SFHs. The approach of Podorvanyuk et al. (2013) allows the IMF slope at the low mass end to be a free parameter in the library of models generated and fit to the observed pixel colours, in principle allowing the IMF to be inferred within spatially resolved galaxy images. Geha et al. (2013) use resolved star counts of two nearby ultra-faint dwarf galaxies to determine αl = −1.2−0.4+0.5 (Hercules) and αl = −1.3 ± 0.8 (Leo IV) in the mass range 0.52 ≤ m / M⊙ ≤ 0.77, and argue that, in combination with resolved star counts from the Milky Way, SMC and Ursa Minor, this suggests a trend to flatter low mass IMF slopes (or increasing mc) for systems with lower velocity dispersion and metallicity, qualitatively consistent with the broad results seen for early type galaxies summarised above (e.g., van Dokkum & Conroy, 2012).
As with the star forming galaxies, the range of analyses of passive galaxies reveal a broadly consistent picture, finding an increased abundance of low mass stars for higher velocity dispersion, or higher metallicity, galaxies, and potentially with this excess located preferentially in the galaxy cores. These IMF variations for passive galaxies do seem to contradict the sense of the variation found for star forming galaxies, a point that I return to below. It would also be interesting to explore the extent to which the recent generation of integral field spectroscopic surveys may be able to bridge the two, applying techniques so far used only for star forming galaxies but instead looking at passive systems with some residual star formation. With spatially resolved spectra, any AGN contributions may be identified and excluded to isolate star formation signatures in otherwise passive galaxies (e.g., Hampton et al., 2017, Medling et al., 2018), allowing the Kennicutt (1983) and related approaches to be applied.
It is clear that analyses of the star forming and passive galaxy populations have a rather different focus in terms of the IMF, of necessity, due to the available observational metrics. Work on the star forming galaxy population has focused on the high mass end of the IMF, and its potential dependence on luminosity, SFR, or SFR (surface) density, loosely characterised as star formation intensity. Analysis of the passive galaxy population, instead, has focused on the low mass end of the IMF. The stars being probed in these systems are only the low mass stars remaining from star formation episodes many Gyr earlier, analogous to the PDMF in Milky Way stellar systems. In qualitative terms the results can be summarised as:
There is a range of uncertainty, quantitative difference, and scatter around these general conclusions, but the broad picture seems to be well established given the observational approaches used.
This broad picture leads to an apparent tension, though, because at first glance the two qualitative results seem inconsistent. The stellar population in the centres of passive galaxies, that formed at the peak of cosmic star formation (z ≈ 2, e.g., Hopkins, 2004, Hopkins & Beacom, 2006), have a relative excess of low mass stars (that may be characterised broadly as α < −2.35), while the star forming galaxies seem to imply that high star formation is associated with a relative excess of high mass stars (similarly characterised broadly by α > −2.35). Are these results actually inconsistent or not? If the IMF is not universal, they are not necessarily inconsistent, as it may be the case that different physical conditions prevailed in the progenitors of high mass elliptical galaxy nuclei, than seen now in high SFR galaxies at low redshift. The question needs to be answered by exploring the physical properties dominating the origin of a particular stellar mass distribution, and the physical conditions prevailing in the different systems at the time of star formation. This is reviewed in § 7 below.
Before delving into those issues, it is worth questioning the robustness of the various observational approaches, and assessing the degree to which they may be systematically biased.
In each case, SPS models play a crucial role in the way an IMF slope is inferred. There are some fundamental limitations in even the most sophisticated modern SPS models, each of which focuses on one particular area of strength but without necessarily incorporating other facets, or coarsely modeling them in the interests of computational efficiency. Two main limitations are the neglect of stellar rotation (e.g., Brott et al., 2011a, Brott et al., 2011b, Levesque et al., 2012, Leitherer et al., 2014) and stellar multiplicity (e.g., Eldridge, 2012, Eldridge et al., 2017). These effects are not negligible, with perhaps up to 30% of high mass main sequence stars produced through binary interaction (Sana et al., 2012, de Mink et al., 2014). Binarity and stellar rotation may reinforce each other in some observable properties, as the modeling of binaries can provide effects similar to the inclusion of stellar rotation for single stars (Leitherer, 2011). In particular, extreme rotation can lead to an increase in the Hα equivalent width by up to an order of magnitude compared to the assumption of no rotation, for the same SFH, in a window between 106.5 < t / yr < 107 (Leitherer et al., 2014). This may lead to a need to reduce inferred SFRs (for example) in some analyses, and may well have an impact on inferred IMFs. Binaries add an extra dimension too, as binary mergers and mass transfer can lead to the presence of stars of higher mass than those in the initial population (Eldridge, 2012, Banerjee et al., 2012). For example, using a binary population synthesis approach Suda et al. (2013) make the case for the Milky Way having an IMF dominated by high mass stars at early times, subsequently evolving to the presently observed IMF, based on observations of CEMP stars. They note that in chemical evolution models the current Milky Way IMF would overpredict Type 1.5 SNe. While observational constraints on the degree of rotation and binarity (or multiplicity) fraction are challenging, it is clear that it is necessary to address these effects in refining any estimated IMFs.
It is also worth noting that the SPS models used to analyse star forming galaxies are typically different from those used to analyse passive galaxies, again for the obvious reason that different codes focus on producing different diagnostics. It would be highly desirable to be able to cross-compare results between the two galaxy populations using a common SPS tool to eliminate any possibility that inconsistent conclusions regarding the IMF are related to SPS model systematics.
SPS models commonly used in the analysis of star forming galaxies include PEGASE (Fioc & Rocca-Volmerange, 1997), STARBURST99 (Leitherer et al., 1999), and GALAXEV, (Bruzual & Charlot, 2003), as well as those incorporating a greater contribution from TP-AGB stars (Maraston, 2005). The conclusions regarding IMF properties in star forming galaxies are generally consistent between these different models, and authors often check that their results are not strongly dependent on the SPS model used (e.g., Meurer et al., 2009, Gunawardhana et al., 2011). Nanayakkara et al. (2017) compared various diagnostics between the PEGASE, STARBURST99 and BPASS (Stanway et al., 2016) SPS tools, to confirm that their results were not sensitive to the choice of SPS model.
In the analysis of passive galaxies, the two dominant SPS tools are the FSPS code of Conroy et al. (2009) and its recent variants (Conroy et al., 2017), and that of Vazdekis (1999) and its recent variants (Vazdekis et al., 2010, Vazdekis et al., 2012) based on the MILES/MIUSCAT empirical stellar spectral libraries. The higher resolution of these libraries is important for constraining the key absorption features sensitive to the low mass stellar populations. Analyses using the former tend to be cast in terms of single power-law IMF slopes, while those of the latter explore both single and double power-law forms. Broadly, both approaches tend to conclude that high mass (or high metallicity) early type galaxies have a need for IMFs with a relative excess of low mass stars, although this is achieved with different IMF forms depending on the SPS tool used for the analysis. Either a single power-law IMF with a slope steeper than Salpeter (α < −2.35) or a double power-law with a steep high mass (m > 0.6 M⊙) slope, both leading to an excess of stars for m < 1 M⊙ compared to Milky Way type IMFs of Kroupa (2001) or Chabrier (2003b). Spiniello et al. (2015b) compare these two SPS models explicitly, and conclude that, while quantitatively different, the result implying an excess of low mass stars for early type galaxies is qualitatively consistent between the two. Conroy (2013) reviews SPS techniques and discusses what can reliably be measured. In this comprehensive review, issues of assumed metallicity and abundances, dust obscuration, SFHs, and stellar evolution libraries are addressed. In particular, Conroy (2013) describes the impact on inferred IMFs arising from limitations in SPS models in his § 7. He focuses primarily on the results arising from the passive galaxy analyses, concluding that modest IMF variations are supported, as inferred through Υ* variations of a factor of 2−3. He briefly argues that the case for “top-heavy” IMFs is not compelling, and does not explore the impact of SPS assumptions in those analyses.
Other potential issues affecting the use of the dwarf-to-giant ratio sensitive features are rare stellar populations and parameter degeneracies. Maccarone (2014) argue, for example, that barium stars and extrinsic S stars can explain the effects seen in the Wing-Ford band and the Na i D absorption features, without needing to invoke varying IMFs. Tang & Worthey (2015) highlight strong degeneracies between the inferred IMF slope and the value of ml, the extent of AGB populations and variations in elemental abundances. They note that “increasing evidence shows that single-burst, single-composition stellar populations oversimplify the underlying stellar systems” and conclude that it is very difficult to disentangle a steepening of the IMF slope from a decreased contribution of the AGB population in young metal-rich galaxies. They note that this degeneracy can be addressed using sufficiently high precision photometry and spectroscopy for old (10 Gyr) metal-rich populations. Similarly, Smith et al. (2015b) used composite J-band spectra compiled from over 100 galaxies to show that it is not possible to jointly constrain the Na abundance and the IMF slope in the most massive galaxies. They conclude by cautioning against over-reliance on Na lines in such studies.
Another limitation was highlighted by Smith (2014), who analysed the dynamical and SPS IMF constraints for 34 galaxies in common between those used by Conroy & van Dokkum (2012) and Cappellari et al. (2013). He found that while the general results of each are consistent, there is no correlation of the IMF inferred on a galaxy-by-galaxy level between the two approaches. He argues that the results of Conroy & van Dokkum (2012) are explained by a trend with Mg/Fe rather than σ, (perhaps qualitatively in line with Martín-Navarro et al., 2015d), but that Cappellari et al. (2013) finds no such relation. He concludes that a range of confounding factors (dark matter contributions or abundance patterns) have not been disentangled from the IMF effects in one or both of the methods. Interestingly, Oldham & Auger (2016) show for M87 that introducing radial stellar anisotropy has a strong impact on the derived M/L, and that this leads to an inferred IMF consistent with Chabrier (2003a), although neglecting the anisotropy would lead to a value of Υ* that implies a Salpeter-like IMF over 0.1 < m / M⊙ < 100.
It is also the case that many samples analysed to date are, in most cases, limited in number to a few tens or in some cases hundreds of galaxies. Although observationally challenging, there is clearly scope for exploring large volume-limited or mass-limited samples, as done by Gunawardhana et al. (2011) for example, in order to account for systematics and selection effects when interpreting any putative physical dependencies for potential IMF variations.
5.5. Linking galaxies to their constituents
The link between the IMF for stars or star clusters and that inferred for galaxies has been explored extensively in the framework of the IGIMF (Kroupa & Weidner, 2003, Weidner & Kroupa, 2005, Kroupa et al., 2013). Bastian et al. (2010) nicely summarise the link between the IGIMF and the relation between mu and cluster mass (Weidner et al., 2010), noting that the evidence for this relation is mixed (but see, e.g., Ramírez Alegría et al., 2016, Stephens et al., 2017). It is worth a brief diversion here to consider a direct comparison between potential variations in the IMF for star clusters and that for galaxies, to test whether there are physical dependencies that may be consistent. From the summary of Bastian et al. (2010), their Figure 2 has a suggestion that star clusters tend to have a somewhat flatter high mass IMF slope (m > 1 M⊙) than found in associations or the field. Can this be characterised as a function of SFR or velocity dispersion, perhaps, to compare against the results from integrated galaxy measurements?
It is not straightforward, it turns out, to compare star forming clusters directly with galaxies. The young massive star forming cluster Westerlund 1 in the Milky Way, for example, has αh = −2.3 for stars in the mass range 3.4 < m / M⊙ < 27 (Brandner et al., 2008). To compare this with the star forming galaxies of Gunawardhana et al. (2011), say, we need to estimate one or more of its SFR, sSFR or SFR surface density (Σ*). Brandner et al. (2008) quote a total initial stellar mass for Westerlund 1 of m ≈ 52000 M⊙, an age of t ≈ 3.6 Myr, and they measured the IMF in annuli extending out to r = 3.3 pc. We can make use of these estimates by way of illustration, although the similarity of values for the other starburst clusters in the Milky Way (Brandner, 2008) lead to the same conclusions. Using the values above, SFR = 0.014 M⊙ yr−1, and Σ* ≈ 400 M⊙ yr−1 kpc−2 for Westerlund 1. It is apparent that the sSFR (defined as the SFR divided by the total stellar mass, for a galaxy) is not really a meaningful quantity here, since the total stellar mass is the same as the stellar mass formed in the star formation event, and would simply equal the inverse of the age for the cluster. This is a hint that such comparisons are not easily made, quickly supported by the fact that the SFR surface density is two orders of magnitude higher than seen in the ensemble of galaxies sampled by Gunawardhana et al. (2011), where −2.7 ≲ log(Σ* / M⊙ yr−1 kpc−2) ≲ −0.8. Clearly the average Σ* for a galaxy is reduced by the many regions that have no ongoing star formation. Alternatively, we could artificially define a larger area encompassing Westerlund 1 that extends out to the boundary with the closest neighbouring star forming system in order to define the value of Σ*, but that opens a host of related questions for how to define such a region. That leaves the direct measure of SFR itself. Here again the comparisons are not straightforward, since now the quantity for Westerlund 1 is two orders of magnitude lower than the range of SFR seen in the galaxies (0 ≲ log(SFR / M⊙ yr−1) ≲ 1.7), unsurprisingly when comparing a single star cluster to a whole galaxy. If instead the stellar velocity dispersion is used as the linking factor, star clusters again have σ substantially lower than those of galaxies. The super star clusters in M82, for example, have 10 ≲ σ / km s−1 ≲ 35 (McCrady & Graham, 2007), compared to the range of 100 ≲ σ / km s−1 ≲ 350 for the early type galaxies in the analyses described above. Said another way, approaches that parameterise the IMF as a function of SFR or σ only make sense in the case of an entire galaxy where such parameters themselves are well-defined. Any relation between the IMF and these parameters must actually reflect an underlying physical dependence on a truly local quantity such as the gas density, ionisation background, or volume density of SFR, for example.
One approach that may have potential in linking the two is that of Zaritsky et al. (2014b), using the stellar M/L ratio, Υ*, scaled to a common 10 Gyr age, and which they denote Υ*,10. As described in § 3.2 above, Zaritsky et al. (2014b) directly compares Υ*,10 for early type galaxies and disk galaxies, showing a general match with the values they identify for the two populations of star clusters. They argue that the different values of Υ*,10 for the two populations reflect variations in the underlying IMF, but that there is no characteristic physical property identified yet that maps to these IMF differences, having ruled out velocity dispersion, surface brightness, half-light radius, metallicity, age, half-mass relaxation time, central luminosity and mass densities, escape speed, binding energy, and more. Despite this lack of a clear physical origin, the use of Υ*,10 as a metric to compare galaxies with stellar clusters deserves further attention.
If the potential physical dependencies of the IMF for a star cluster cannot be directly compared to those for a galaxy, this reintroduces the concern about the IMF itself being a poorly-posed concept, to which I return in §§ 8 and 9 below.
Continuing to increase in scale, I turn next to the constraints on the IMF that have been explored through galaxy populations, rather than individual systems.