


Mateo et al. (1993) noticed that dSph dynamical mass-to-light ratios increase monotonically with decreasing luminosity (left panel of Figure 17). Based on mass-follows-light analyses (Section 4.1.1), the Milky Way's eight classical dSphs trace a relationship log10(M / LV / [M / LV]⊙) ∼ 2.5 + 107 LV / LV,⊙ (Mateo, 1998). This relation implies that if their stellar mass-to-light ratios are M / LV ∼ 2.5[M / LV]⊙, then each dSph is embedded in a dark matter halo of mass ∼ 107 M⊙. Allowing for extended dark matter halos, Mateo et al. (1993) and Mateo (1998) interpret this value as the minimum mass that is associated empirically with dark matter.
Kinematic studies of the newfound ultrafaint satellites alter this picture slightly. The ultrafaint dSphs extend the luminosity floor from MV ∼ −9 (e.g., Draco, Ursa Minor) to MV ∼ −2 (e.g., Segue 1), nearly three orders of magnitude in luminosity. Applying mass-follows-light models to their velocity data for the least luminous dSphs, Martin et al. (2007) and Simon & Geha (2007) estimate dynamical masses as small as ∼ 105 M⊙. While these masses imply extreme mass-to-light ratios M / LV ≳ 100 [M / LV]⊙ that extend the monotonic increase in M / LV with decreasing luminosity, they suggest that this relationship becomes flatter toward the smallest luminosities (right panel of Figure 17).
Strigari et al. (2008a) extend to ultrafaint satellites the notion of a common dSph mass by considering the amount of mass enclosed within a fixed radius of 300 pc (implicitly assuming that all dSphs occupy dark matter halos at least this large). Using a Jeans analysis similar to that described in Section 4.1.3, Strigari et al. (2008a) estimate M300 ≡ M(r ≤ 300 pc) ∼ 107 M⊙ for dSphs spanning five orders of magnitude in luminosity (Figure 20, left panel). Walker et al. (2009b) take a different approach, using the model-independent estimates of M(Rh) provided by Equation 15 to evaluate the hypothesis that all dSphs are embedded in identical dark matter halos characterised by a ‘universal’ mass profile (Figure 20, right panel). While the scatter of M(Rh) values about a single power law, M(r) ∝ rx, is larger (by a factor of ∼ 2) than the scatter expected to arise from observational errors, it is similar to the scatter about a common value of M300.
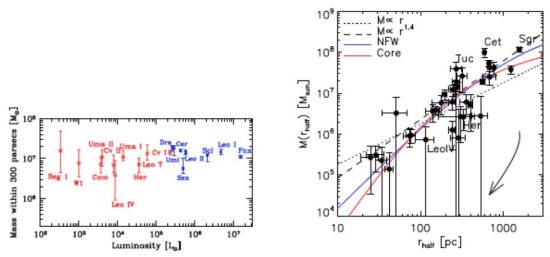 |
Figure 20. A common mass? Left: mass enclosed within a radius of r≤ 300 pc, estimated from a Jeans analysis (See Section 4.1.3), versus luminosity (Strigari et al., 2008a, reproduced with permission). Right: mass enclosed within the projected halflight radius, estimated from Equation 15, versus halflight radius (Walker et al., 2009b, reproduced by permission of the American Astronomical Society). Arrows indicate the trajectory followed by a satellites as they lose up to 99% of their original stellar mass, from N-body simulations by Peñarrubia et al. (2008). Overplotted are various dark matter halo models (Walker et al., 2009b). |
While it has long been known that dSphs do not fit naturally onto scaling relations defined by larger elliptical galaxies (e.g., Kormendy, 1985), the roughly exponential decline of dSph surface brightness profiles (Section 2.2.1) hints at a structural relationship to spirals (Faber & Lin, 1983, Lin & Faber, 1983), perhaps via an evolutionary mechanism such as tidal stirring (Sections 2.2.1, Mayer et al. 2001a, b). Converting estimates of M(Rh) to circular velocities vcirc2 = GM(Rh) / Rh, Walker et al. (2010) find that the Milky Way's dsph satellites lie on an extrapolation of the mean rotation curve estimated for dark matter in spiral galaxies (Figure 21, left panel), log10[Vcirc / (km s−1)] = 1.5 + 0.5 log10[r / kpc] (McGaugh et al., 2007). Donato et al. (2009) and Salucci et al. (2011) find similar results: assuming cored dark matter halos of the form ρ(r) = ρ0 r03(r + r0)−1(r2 + r02)−1 (Burkert, 1995), fits to dSph velocity dispersion profiles extend a simple scaling relationship that is common to spiral galaxies (Kormendy & Freeman, 2004) and is characterised by log10[ρ0 / (M⊙ pc−3) r0 / pc] ∼ 2, independently of luminosity (Figure 21, right panel).
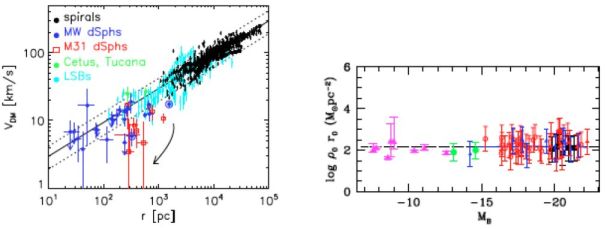 |
Figure 21. Similarity with spiral galaxies (Section 5)? Left: circular velocities (vcirc = √GM(Rh) / Rh) for the Milky Way's dSph satellites lie on the extrapolation of the mean rotation curve due to dark matter in spiral (McGaugh et al., 2007) and low surface brightness (Kuzio de Naray et al., 2008) galaxies (Walker et al., 2010, reproduced by permission of the American Astronomical Society). Right: Dark matter surface densities inferred from fits of Burkert (1995) halos have the same constant value inferred from spiral galaxy rotation curves (reproduced from Dwarf Spheroidal Galaxy Kinematics and Spiral Scaling Laws, by P. Salucci et al., MNRAS, in press, by permission of John Wiley & Sons Ltd.). |
These scaling relationships have provoked a variety of disparate interpretations. For example, Boyarsky et al. (2010a) show analytically that ‘secondary infall’ of dark matter onto isolated halos would cause surface density to vary slowly with halo mass, explaining the apparent constancy of ρ0 r0 over the range spanned by spirals. They argue that the apparent extension to dSphs agrees with results from cosmological N-body simulations (e.g., Springel et al., 2008), which produce satellite halos with approximately the same surface density. On the other hand, McGaugh & Wolf (2010) show that dSphs deviate from another spiral scaling relation — the baryonic Tully-Fisher relation (‘BTF’, McGaugh et al., 2000) — systematically according to the amount by which their halflight radii exceed their tidal radii, provided that the latter radius is estimated using Milgrom's (1983) Modified Newtonian Dynamics (a framework that naturally implies the BTF relation).
In any case, scatter among the Milky Way's dSphs increased when Adén et al. (2009) and Koposov et al. (2011b) measured smaller velocity dispersions for Hercules and Boötes I, respectively, than had previously been estimated (Section 2.3). Furthermore, early kinematic results for the dSph satellites of M31 suggest systematically smaller masses (at a given halflight radius) than estimated for the Milky Way dSphs (Kalirai et al., 2010, Collins et al., 2010, 2011). However, more recent, larger data sets suggest that the M31 dSphs are more similar to the MW dSphs than previously suggested (Tollerud et al., 2011). Pending more detailed spectroscopic surveys, particularly of the least luminous and most distant dSphs, the interpretation of scaling relationships that connect galaxies across such wide ranges of luminosity and morphological type should proceed with caution.