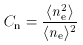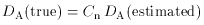The simplest cosmological use of the Sunyaev-Zel'dovich effect is to prove
that the CMBR is genuinely a cosmological phenomenon: the appearance
of an effect from a cluster of galaxies at z = 0.5455
(CL 0016+16) proves that the CMBR originates at z > 0.54,
higher-redshift detections push this limit even further. However, it is
as a probe of cosmological parameters, and as a distance-independent
probe of earlier phases of the Universe that the Sunyaev-Zel'dovich
effect has attracted most interest, and such uses of the effect are the
focus of this section.
11.1
Cosmological parameters
The basis of the use of the Sunyaev-Zel'dovich effect as a tracer of cosmological parameters was given in Sec. 4.1. The essence of the idea is the same as for other distance-measuring techniques that depend on a comparison of the emission and absorption of radiation from gas: the surface brightness of the gas in emission is proportional to the line-of-sight integral of some density squared,
while the absorption of some background source of radiation is
proportional to the optical depth
Thus if both the emission from the gas, E, and its absorption,
A, can be measured, the quantity A2 / E is
a density-weighted measure of
the path-length through the gas. If the structure of the gas is known,
and its angular size,
Although this technique may eventually be applied using only X-ray data
(Krolik & Raymond 1988),
it is currently used
for the measurement of distances using a combination of X-ray and
the Sunyaev-Zel'dovich effect data
(Gunn 1978;
Silk & White 1978;
Birkinshaw 1979;
Cavaliere et al. 1979).
The emission of
gas in a cluster of galaxies is measured by its X-ray surface brightness,
where
at dimensionless frequency x = h
with s = ln (x / x0)
(see Secs 3.2
and 3.3; this form is used by Holzapfel
et al. 1997a).
Since the technique compares the angular size of a cluster of galaxies
with a measure of the line-of-sight size of the cluster, it is
important to have a model for the structure of the gas so that the
relationship between the projected quantities bX and
and the energy loss and spectrum functions may be written
in terms of similar form factors which depend on fn
and fT in complicated ways,
(Birkinshaw et
al. 1991;
Holzapfel et
al. 1997a).
The X-ray surface
brightness and the thermal Sunyaev-Zel'dovich effect intensity change
can then be
expressed in terms of physical constants and angular structure
factors, as
with the structural information for the cluster contained in the
angles
which describe the shapes of the X-ray and Sunyaev-Zel'dovich effects
that the model
gas distribution would produce.
An absolute distance for a cluster is then found by fitting the X-ray and
Sunyaev-Zel'dovich effect data to models of the form (113)
and (114) to deduce NX and NSZ, and
calculating the angular diameter distance using
(Holzapfel et
al. 1997a),
or equivalently from the form given by
Birkinshaw et
al. (1991)
in their
equation 39, if brightness temperature rather than intensity is used
as the Sunyaev-Zel'dovich effect observable. The value of the Hubble
constant is
then obtained from the measured redshift of the cluster and the value
of DA under some assumption about the value of
q0 using equation (71).
This is a direct method of measuring the distance of a cluster
of galaxies and the value of the Hubble constant: it can be applied at
large cosmological distances without any intervening chain of distance
estimators (as in the usual distance ladder). The distance
estimate relies on simple physics - the properties of a fully-ionized
gas held nearly in hydrostatic equilibrium in the gravitational
potential well of a cluster of galaxies. The basis of this distance
estimate can therefore be tested by making a detailed study of the
properties of the cluster being used as a cosmological tracer and the
population of similar clusters. It is also important that
in this method each cluster of galaxies is treated as an individual
- the evolutionary peculiarities of a distant cluster need not
affect the distance estimate provided that the physical state of the
intracluster gas is understood. Of course, if the cluster gas has much
small-scale density and temperature structure, it may be difficult
to obtain good models for the form factors (109) - (112), and there
may be a substantial systematic error in the distance estimate. Some
protection against this systematic error can be obtained by cross-checking
the independent results that are obtained from a number of clusters.
The measurement of the values of NX and
NSZ from the
X-ray and Sunyaev-Zel'dovich effect data not only requires knowledge of
the form factors
fn, fT, f
Rephaeli & Yankovitch
(1997)
have recently pointed out
that for good accuracy in calculating cluster distances in this way,
it is important to the full relativistic formalism
(Gould 1980)
to calculate the value of
A convenient form that has been used to describe the structure of
cluster atmospheres is the spherical isothermal beta model
(equation 64), with constant electron temperature and a
concentration form factor
The quantity
which must then be convolved with the responses of the telescopes to
calculate the structures that would be seen in practice.
Values of
Values of the Hubble constant based on this distance estimation
technique are now available for nine clusters. For the clusters
with Sunyaev-Zel'dovich effects shown in
Fig. 17,
19,
22 and
23, a
detailed discussion of the fitting procedures used is given by
Birkinshaw et
al. (1991),
Birkinshaw & Hughes
(1994),
Jones (1995),
Holzapfel et
al. (1997a), and
Hughes & Birkinshaw
(1998).
The distances estimated for all
nine clusters are displayed as luminosity distances as a function of
redshift in Fig. 25. The error bars on the distance
estimates are symmetrized errors taken from the individual papers and
include systematic errors as well as random errors from uncertainties
in the data.
If the results in Fig. 25 are taken at face value,
the measurements suggest a Hubble constant near 60 km s-1
Mpc-1, and
have a scatter of about ± 20 km s-1 Mpc-1
(see the similar analysis of
Furuzawa 1996).
However, we
cannot use this to conclude that H0 = 60 ± 10 km
s-1 Mpc-1, as seems
reasonable based on nine~measurements, since those measurements are not
truly independent. In particular, only three different telescopes were
used in the measurement of NSZ and only two in the
measurement of NX, so that there are only about two
independent X-ray calibrations and three independent Sunyaev-Zel'dovich effect
calibrations in the set of results for H0. An
improvement in the precision of the determination of
H0, even in the absence of any
other problems, must depend on convincing absolute calibrations of
the Sunyaev-Zel'dovich effect and X-ray data.
There are a number of other systematic problems in using this technique.
The most serious may be a selection effect, which causes the value of
H0 to be biased low. If the model (118) for
fn is
modified to make the cluster atmosphere prolate or oblate, then the
apparent X-ray and Sunyaev-Zel'dovich effect images of a cluster will be
ellipsoidal, or circular if the symmetry axis lies along the line of
sight. In the latter case it is clear that it will not be possible to
tell that the cluster is aspherical based on the images: indeed, if
the core radius of the gas distribution on the line of sight is larger
by a factor Z than the core radii in the other two directions, then
the density form factor becomes
and the expressions for
if the distance is estimated using (117) not knowing that the
cluster is elongated on the line of sight.
An indication of the importance of this effect is shown in
Fig. 26, where the estimated value for the Hubble
constant from CL 0016+16 is shown as a function of the intrinsic
ellipticity (axial ratio) of an ellipsoidal model for the gas
distribution. An ellipsoidal model is clearly preferred because of
the non-circular X-ray and Sunyaev-Zel'dovich effect isophotes
(Figs. 2,
23). The value of the
Hubble constant derived by fitting the
cluster by a spherical isothermal model is 68 km s-1
Mpc-1: it
can be seen from the figure that by allowing ellipsoidal models with
axial ratios as large as
2:1, values over the range 40-100 km s-1 Mpc-1 can
be obtained.
In order to avoid the selection bias in favor of clusters which are
elongated along the line of sight, and hence of high surface
brightness, and for which low estimates of the Hubble constant are
produced, this technique must be applied to a sample of clusters
selected without regard to their central surface brightness -
perhaps clusters with total X-ray luminosities or flux densities above
some limiting value. Such a selection is now possible using the
high-sensitivity survey data recently returned by ROSAT (e.g.,
Ebeling et al.
1996).
A corollary is that clusters which are
intrinsically hard to study in the X-ray or the Sunyaev-Zel'dovich effect (and
including Sunyaev-Zel'dovich effect non-detections) must be included in
the set used to measure H0: the clusters with the
weakest Sunyaev-Zel'dovich effects for their
measured X-ray brightnesses are exactly those which imply larger
values of H0 (albeit with larger observational errors). By
contrast, the clusters in Fig. 25 were often selected
based on having particularly strong Sunyaev-Zel'dovich effects, and are
therefore
likely to show an orientation bias. The size of this bias is not known
at present, but is probably less than 30 per cent based on the
distribution of X-ray axial ratios seen in other cluster samples.
In addition to this bias, there is a further contribution to the error
in the estimated distance from the unknown intrinsic shape of cluster
atmospheres. The range of observed shapes suggests an error of order
20 per cent is possible
(Hughes & Birkinshaw
1998),
and calculations of the evolution of cluster atmospheres confirm that
this error estimate is reasonable
(Roettiger et al. 1997;
Yoshikawa et al. 1998).
A major component of the error in the estimates of the normalizations
often arises from uncertainties in the parameters of the model
(equation 121 or some more complicated function). This is
particularly evident when the fits are based on older X-ray data (as,
for example,
Birkinshaw & Hughes
1994).
The more
recent X-ray imaging data from ROSAT substantially reduce the
allowable range of parameters
Modeling the gas appropriately is important because it is not the
same gas that is responsible for the X-ray and Sunyaev-Zel'dovich effect
signals
that are used to determine the distance. The
X-ray surface brightness is dominated by the densest parts of the
cluster, since the X-ray emissivity of the gas is proportional to
ne2 Te1/2, while the
Sunyaev-Zel'dovich effect is dominated by
the lower-density and hotter parts of the gas where the path lengths
are longest. This effect is particularly important where single-dish
measurements of the Sunyaev-Zel'dovich effect are used, while
interferometer maps
tend to resolve out structures on the largest angular scales.
Uncertainties in the relationship between the contributions of low
and high-density regions to the X-ray surface brightness
and the Sunyaev-Zel'dovich effect can be avoided by making deep X-ray images,
which trace the gas to sufficiently large radii that 90 or 95 per
cent of the gas responsible for the Sunyaev-Zel'dovich effect is included. This
means, however, tracing the cluster X-ray emission out to at least
10 core radii, at which the surface brightness has fallen to less than
10-3 of its central value, which often requires long integration
times and careful treatment of the background in the X-ray detectors.
Thermal structure in the cluster atmosphere is harder to measure, and
to achieve good accuracy in the distance estimates it is necessary to
know about the temperature of the cluster gas out to 10 core
radii. This is difficult, not only because of the
low surface brightnesses of clusters at such radii, but also because
of the lower angular resolution
of X-ray detectors with useful spectral response. There is
little clear information on the changes in temperature of cluster
gas as a
function of radius outside a few core radii, and an isothermal model
(or sometimes a temperature model based on a bright nearby cluster,
such as Coma; equation 73) are usually
assumed. Systematic errors at the ten per cent level are likely from
this uncertainty, and larger errors are possible for more extreme
temperature profiles - hydrodynamical models of the evolution of
cluster atmospheres
(Roettiger et
al. 1997;
Yoshikawa et
al. 1998)
suggest that systematic errors of as much
as 30 per cent and random errors of order 10 per cent in the Hubble
constant may arise because of departures from isothermality.
A different type of density and temperature structure is often found
in the central parts of clusters, where the high X-ray emissivity
causes the cooling time of the gas to be short. The consequent
decrease in central pressure causes a ``cooling flow'' to be
established, with a slow inward drift of the atmosphere, an increase
in the central X-ray surface brightness, and a decrease in the central
gas temperature (e.g.,
Fabian et al.
1984).
Since the
central region in which there is a large change of gas properties is
fairly small, it is still possible to use a model of the form
(118) to describe the gas distribution, provided that
the central X-ray brightness spike is excluded from the X-ray fit, and
a corresponding change is made to the fitting for the Sunyaev-Zel'dovich
effect. The
Sunyaev-Zel'dovich effect will show less modification than the X-ray surface
brightness in the presence of a cooling flow because the path length
through the cooling region is relatively small, and there is only a
small change of electron pressure in that region. However, the cooling
gas may partly ``fill in'' the cm-wave microwave background diminution
with free-free emission
(Schlickeiser 1991),
so that
excluding the central region of a cluster from the fit may be important.
Even smaller-scale structure in cluster atmospheres can have an
effect on the derived distance. If the intracluster gas is isothermal,
but shows density clumping on a scale less than the resolution of the
images, then the X-ray emissivity of a small element of gas is
enhanced by a factor
while the value of < ne > is
unchanged. Thus the cluster generates more X-ray emission than would
be expected based on a uniform atmosphere, and hence the true
angular diameter distance is
so that with Cn > 1, the true value of the Hubble
constant is smaller than the value estimated based on (117) without
knowledge of the small-scale clumping.
Unlike the orientation bias, where averaging over a large number of
clusters in random orientations with a known distribution of cluster
shapes can correct the distance estimate, all cluster
atmospheres are expected to be clumpy to some degree, and it is
necessary to estimate the value of the clumping in the ``average''
cluster atmosphere, or to measure it in each cluster, in order to be
sure that the distance estimate is not seriously in error. A
theoretical estimate of the degree of clumping of the intracluster
medium would be difficult, since it must take into account the
processes that cause clumping (such as gas injection from the
galaxies and energy input from galaxy motions) and that erase clumping
(thermal conduction, gas-dynamical processes, and so on).
If the clumping is strong and non-isothermal, then detailed X-ray
spectroscopy may be able to measure the distribution of
temperatures within a cluster, but it is unlikely that full account
could be taken of a distribution of Cn (with an associated
form factor, fC) over the cluster volume, nor that the
full range
of types of clumping could be tested in this way. At present it
appears that the clumping of the intracluster medium is relatively
weak, since if Cn is often large, then it would be expected
to show significant variation from cluster to cluster, and the Hubble
diagram (Fig. 25)
would show stronger scatter than it does. However, the errors on the
distance estimates in Fig. 25 at present cannot
exclude values of Cn ~ 1.5, with consequent large
systematic error in H0.
A variety of other potential problems with this method can be
imagined. The Sunyaev-Zel'dovich effect signal could be contaminated by
a background
primordial anisotropy in the microwave background radiation (e.g.,
Cen 1998),
or by the non-thermal Sunyaev-Zel'dovich effect of a
cluster radio halo source, or by the kinematic Sunyaev-Zel'dovich
effect, or by diffuse radio emission from cool gas (perhaps clumped
into a population of spiral galaxies) towards the edge of the
cluster. The X-ray signal could also be contaminated, perhaps by
the inverse-Compton emission of relativistic electrons
in the cluster radio halo source.
Some of these effects are one-sided biases in the distance
estimate, others would increase scatter in the Hubble diagram, but in
general they should provide additional errors at the level of 10 per
cent or less in the distance estimate
(Birkinshaw et
al. 1991;
Holzapfel et
al. 1997a).
The potential of this method for measuring the Hubble constant is only
now starting to be realized, as better Sunyaev-Zel'dovich effect data become
available. I expect a large increase in the number of clusters on a
future Hubble diagram like Fig. 25, and that useful
cosmological results will be obtained, especially as the maximum
redshift at which an Sunyaev-Zel'dovich effect cluster is detected
increases above
0.55. However, in view of the likely presence of residual systematic
effects in the data and the low accuracy of any one measurement, I
believe that it is premature to use them to estimate the values
of the deceleration parameter and cosmological constant, as has been
attempted recently by
Kobayashi et al. (1996).
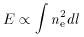
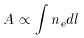
 , can be
measured, then the angular
diameter distance of the gas can be estimated from
A2 / (E
, can be
measured, then the angular
diameter distance of the gas can be estimated from
A2 / (E  ).
).

 e(E,
Te) is the X-ray spectral emissivity
of the cluster gas (Sec. 4.1), while the
absorption by the gas is measured by the thermal Sunyaev-Zel'dovich
effect, which can be expressed as an intensity change
e(E,
Te) is the X-ray spectral emissivity
of the cluster gas (Sec. 4.1), while the
absorption by the gas is measured by the thermal Sunyaev-Zel'dovich
effect, which can be expressed as an intensity change
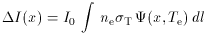
 / kBTrad, where
I0 = (2 h / c2)
[(kBTrad / h)]3 is a
scale intensity and
/ kBTrad, where
I0 = (2 h / c2)
[(kBTrad / h)]3 is a
scale intensity and 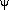 (x,Te) is the dimensionless form of
the frequency-dependent, relativistic, spectrum of the effect (from
equation 51),
(x,Te) is the dimensionless form of
the frequency-dependent, relativistic, spectrum of the effect (from
equation 51),
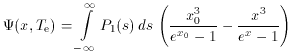
 I can be calculated. It
is convenient to express the electron
concentration and temperature in terms of reference values (chosen as
the central values here, although the values at any fiducial point can
be used) and dimensionless form factors describing the angular
structure of the gas in density, fn(
I can be calculated. It
is convenient to express the electron
concentration and temperature in terms of reference values (chosen as
the central values here, although the values at any fiducial point can
be used) and dimensionless form factors describing the angular
structure of the gas in density, fn( ,
, ,
, ), and
temperature, fT(
), and
temperature, fT( ,
, ,
, ). The angular variables are
). The angular variables are
 , the angle from the reference
line of sight through the
cluster center,
, the angle from the reference
line of sight through the
cluster center,  =
l / DA, an angular
measure of distance down the line of sight, and
=
l / DA, an angular
measure of distance down the line of sight, and  , an azimuthal
angle about the line of sight. DA is the angular diameter
distance of the cluster. Then the electron density and
temperature at some location, r, are
, an azimuthal
angle about the line of sight. DA is the angular diameter
distance of the cluster. Then the electron density and
temperature at some location, r, are
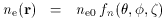
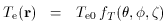
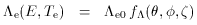
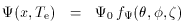
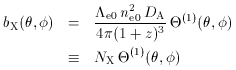
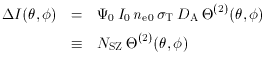


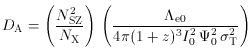
 , and f
, and f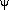 but also the
fiducial electron temperature of the cluster, T0,
since T0 is an implicit variable in (117), where
it enters in both
but also the
fiducial electron temperature of the cluster, T0,
since T0 is an implicit variable in (117), where
it enters in both  e0
and
e0
and 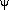 0. Even with the help
of the resolved X-ray spectroscopy that will
become available on the next generation of X-ray telescopes (such as
AXAF), it is not
possible to use the X-ray or Sunyaev-Zel'dovich effect
data to measure these three-dimensional
form factors. Therefore, the calculation proceeds by adopting some
parameterized models for the electron concentration and
temperature as functions of position which are consistent with the
X-ray image and spectroscopy and the Sunyaev-Zel'dovich effect data. The
normalizations NX and NSZ that are
found are then dependent on the unknown structural parameters
of the model atmosphere after any adjustable parameters have been
determined.
0. Even with the help
of the resolved X-ray spectroscopy that will
become available on the next generation of X-ray telescopes (such as
AXAF), it is not
possible to use the X-ray or Sunyaev-Zel'dovich effect
data to measure these three-dimensional
form factors. Therefore, the calculation proceeds by adopting some
parameterized models for the electron concentration and
temperature as functions of position which are consistent with the
X-ray image and spectroscopy and the Sunyaev-Zel'dovich effect data. The
normalizations NX and NSZ that are
found are then dependent on the unknown structural parameters
of the model atmosphere after any adjustable parameters have been
determined.
 e0 and
f
e0 and
f for X-ray
emission from the cluster gas, just as
the relativistic expression for the Sunyaev-Zel'dovich effect
(51) must be used.
Hughes & Birkinshaw
(1998)
have shown that the size of the
relativistic correction in Rephaeli & Yankovitch's work is excessive,
apparently because of their use of an equation containing a
typographical error in
Gould (1980).
Even so,
the size of the relativistic corrections is appreciable (5 per cent or
so) for the hot clusters for which Sunyaev-Zel'dovich effects have been
measured.
for X-ray
emission from the cluster gas, just as
the relativistic expression for the Sunyaev-Zel'dovich effect
(51) must be used.
Hughes & Birkinshaw
(1998)
have shown that the size of the
relativistic correction in Rephaeli & Yankovitch's work is excessive,
apparently because of their use of an equation containing a
typographical error in
Gould (1980).
Even so,
the size of the relativistic corrections is appreciable (5 per cent or
so) for the hot clusters for which Sunyaev-Zel'dovich effects have been
measured.

 c =
rc/DA is the angular equivalent of
the core radius of the atmosphere, rc.
This model leads to simple
expressions for the angles
c =
rc/DA is the angular equivalent of
the core radius of the atmosphere, rc.
This model leads to simple
expressions for the angles  (1) and
(1) and  (2),
(2),
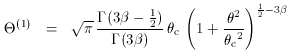
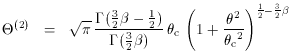

 0.7, and rc
0.7, and rc  150
h100-1 kpc
are typically obtained in fitting X-ray images of clusters to
the structure defined by (113) and (119).
150
h100-1 kpc
are typically obtained in fitting X-ray images of clusters to
the structure defined by (113) and (119).
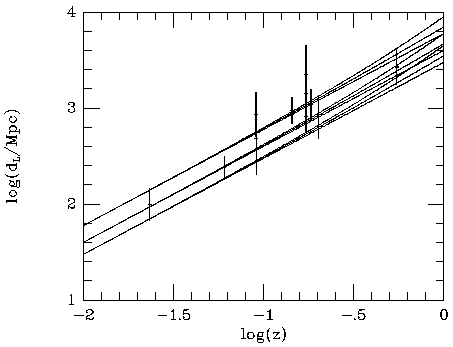
Figure 25. A Hubble diagram based on the distances measured for
the nine clusters Abell 1656, 2256, 478, 2142, 1413, 2163, 2218, and 665 and
CL 0016+16
(Herbig et al.
1995;
Myers et al.
1997;
Grainge 1996;
Holzapfel et
al. 1997a;
McHardy et al.
1990;
Birkinshaw & Hughes 1994;
Jones 1995;
Birkinshaw et
al. 1991;
and Hughes & Birkinshaw 1996).
Three values are
shown for the distance of Abell 2218 (from Birkinshaw & Hughes,
Jones, and McHardy et al.).
The Hubble relation is drawn for H0 = 50, 75, and
100 km s-1 Mpc-1, with q0 = 0,
1/2, and 1. The current best
fit is for a Hubble constant of about 60 km s-1
Mpc-1, with no strong constraint on q0, but
no convincing error can be given because the
distance estimates contain correlated systematic errors arising from
the calibrations used (see text).

 (1) and
(1) and  (2)
(119 and 120) remain valid, while the
normalizations NX and
NSZ both increase by a factor Z. The result is
that a prolate gas
distribution, with the symmetry axis along the line of sight, tends to
give a higher central surface brightness than other gas
distributions in which the same mass of gas
is distributed spherically or with the symmetry axis perpendicular to
the line of sight. This causes clusters elongated along the line of
sight to be easier to detect in the X-ray or in the Sunyaev-Zel'dovich
effect. Such
clusters also give biased estimates of distance, since the true
angular diameter distance is
(2)
(119 and 120) remain valid, while the
normalizations NX and
NSZ both increase by a factor Z. The result is
that a prolate gas
distribution, with the symmetry axis along the line of sight, tends to
give a higher central surface brightness than other gas
distributions in which the same mass of gas
is distributed spherically or with the symmetry axis perpendicular to
the line of sight. This causes clusters elongated along the line of
sight to be easier to detect in the X-ray or in the Sunyaev-Zel'dovich
effect. Such
clusters also give biased estimates of distance, since the true
angular diameter distance is
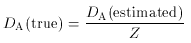
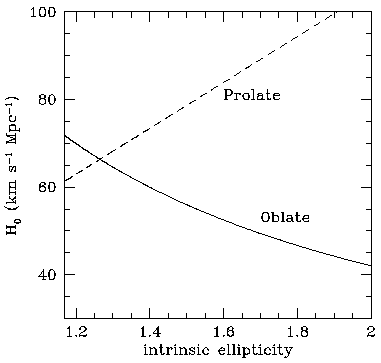
Figure 26. The dependence of the
Hughes & Birkinshaw's
(1998)
estimate
of the value of the Hubble constant on assumptions about the
oblateness or prolateness of CL 0016+16 in the extreme case where the
cluster symmetry axis lies in the plane of the sky.
 and
and  c, so
that this component of the error in the Hubble
constant may be reduced. However, there is an intrinsic uncertainty in
the types of gas model that are chosen to describe the atmosphere, and
the extent to which they fail to represent aspects of the density and
thermal structure of the gas that affect the distance estimate.
c, so
that this component of the error in the Hubble
constant may be reduced. However, there is an intrinsic uncertainty in
the types of gas model that are chosen to describe the atmosphere, and
the extent to which they fail to represent aspects of the density and
thermal structure of the gas that affect the distance estimate.