


9.1. Spectral Methods of Inferring the Reionization Redshift
9.1.1. Cosmology with
Ly Photons
Photons
The scattering cross-section of the
Ly resonance line by neutral
hydrogen is given by (Section 23 of
Peebles 1993)
resonance line by neutral
hydrogen is given by (Section 23 of
Peebles 1993)
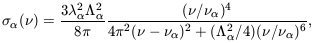
| (107) |
where 
 =
(8
=
(8 2 e2
f
2 e2
f /
3me c
/
3me c
 2) = 6.25 × 108
s-1 is the
Ly
2) = 6.25 × 108
s-1 is the
Ly (2p -> 1s)
decay rate,
f
(2p -> 1s)
decay rate,
f = 0.4162 is the
oscillator strength, and
= 0.4162 is the
oscillator strength, and

 = 1216Å and
= 1216Å and

 = (c /
= (c /

 ) = 2.47 ×
1015 Hz are the wavelength and frequency of the
Ly
) = 2.47 ×
1015 Hz are the wavelength and frequency of the
Ly line. The term in the numerator
is responsible for the classical Rayleigh scattering.
line. The term in the numerator
is responsible for the classical Rayleigh scattering.
We consider a source at a redshift zs beyond the redshift of
reionization (10)
zreion, and the corresponding
scattering optical depth of a uniform, neutral IGM of hydrogen density
nH, 0(1 + z)3 between the source and
the reionization
redshift. The optical depth is a function of the observed wavelength
 obs,
obs,
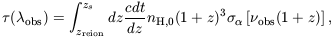
| (108) |
where  obs = c /
obs = c /
 obs and
obs and
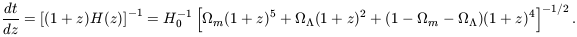
| (109) |
At wavelengths longer than Ly at the source, the optical depth
obtains a small value; these photons redshift away from the line
center along its red wing and never resonate with the line core on
their way to the observer. Considering only the regime in which
|
at the source, the optical depth
obtains a small value; these photons redshift away from the line
center along its red wing and never resonate with the line core on
their way to the observer. Considering only the regime in which
| -
-

 | >>
| >>

 , we may ignore the
second term in the denominator of equation (107). This leads
to an analytical result for the red damping wing of the Gunn-Peterson
trough
(Miralda-Escudé
1998)
, we may ignore the
second term in the denominator of equation (107). This leads
to an analytical result for the red damping wing of the Gunn-Peterson
trough
(Miralda-Escudé
1998)
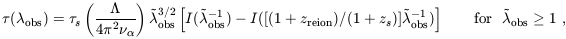
| (110) |
where  s is given in
equation (1), and we also define
s is given in
equation (1), and we also define
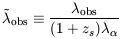
| (111) |
and
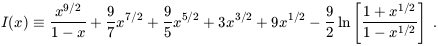
| (112) |
At wavelengths corresponding to the
Ly resonance between the source
redshift and the reionization redshift, (1 + zreion)
resonance between the source
redshift and the reionization redshift, (1 + zreion)



 obs
obs
 (1 + zs)
(1 + zs)

 , the optical depth is
given by equation (1). Since
, the optical depth is
given by equation (1). Since
 s ~ 105,
the flux from
the source is entirely suppressed in this regime. Similarly, the
Ly
s ~ 105,
the flux from
the source is entirely suppressed in this regime. Similarly, the
Ly resonance
produces another trough at wavelengths
(1 + zreion)
resonance
produces another trough at wavelengths
(1 + zreion)




 (1 + zs)
(1 + zs)

 , where
, where

 = (27 / 32)
= (27 / 32)

 = 1026 Å, and the
same applies to the higher Lyman series lines. If
(1 + zs)
= 1026 Å, and the
same applies to the higher Lyman series lines. If
(1 + zs)  1.18(1 + zreion) then
the Ly
1.18(1 + zreion) then
the Ly and the
Ly
and the
Ly resonances
overlap and no flux is transmitted in-between the two troughs (see
Figure 40). The
same holds for the higher Lyman-series resonances down to the Lyman
limit wavelength of
resonances
overlap and no flux is transmitted in-between the two troughs (see
Figure 40). The
same holds for the higher Lyman-series resonances down to the Lyman
limit wavelength of
 c = 912Å.
c = 912Å.
At wavelengths shorter than
 c, the photons
are absorbed when
they photoionize atoms of hydrogen or helium. The bound-free
absorption cross-section from the ground state of a hydrogenic ion
with nuclear charge Z and an ionization threshold
h
c, the photons
are absorbed when
they photoionize atoms of hydrogen or helium. The bound-free
absorption cross-section from the ground state of a hydrogenic ion
with nuclear charge Z and an ionization threshold
h 0, is given by
(Osterbrock 1974),
0, is given by
(Osterbrock 1974),
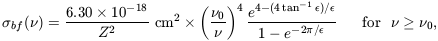
| (113) |
where
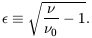
| (114) |
For neutral hydrogen, Z = 1 and
 H, 0 = (c /
H, 0 = (c /
 c) = 3.29
× 1015 Hz
(h
c) = 3.29
× 1015 Hz
(h H, 0 = 13.60 eV); for
singly-ionized helium, Z = 2 and
H, 0 = 13.60 eV); for
singly-ionized helium, Z = 2 and
 HeII, 0 = 1.31 ×
1016 Hz
(h
HeII, 0 = 1.31 ×
1016 Hz
(h HeII, 0 =
54.42 eV). The cross-section
for neutral helium is more complicated; when averaged over its narrow
resonances it can be fitted to an accuracy of a few percent up to
h
HeII, 0 =
54.42 eV). The cross-section
for neutral helium is more complicated; when averaged over its narrow
resonances it can be fitted to an accuracy of a few percent up to
h = 50 keV by the fitting function
(Verner et al. 1996)
= 50 keV by the fitting function
(Verner et al. 1996)
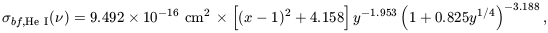
| (115) |
where x  [(
[( / 3.286 × 1015
Hz) - 0.4434], y
/ 3.286 × 1015
Hz) - 0.4434], y  x2 + 4.563, and the threshold for ionization is
x2 + 4.563, and the threshold for ionization is
 HeI, 0 = 5.938 ×
1015 Hz
(h
HeI, 0 = 5.938 ×
1015 Hz
(h HeI, 0 = 24.59 eV).
HeI, 0 = 24.59 eV).
For rough estimates, the average photoionization cross-section for a
mixture of hydrogen and helium with cosmic abundances can be
approximated in the range of
54 < h
 103 eV as
103 eV as
 bf
bf

 0(
0( /
/
 H, 0)-3, where
H, 0)-3, where
 0
0
 6 × 10-17
cm2
(Miralda-Escudé
2000).
The redshift factor in the cross-section then cancels exactly the
redshift evolution of the gas density and the resulting optical depth
depends only on the elapsed cosmic time,
t(zreion) - t(zs). At high
redshifts (equations (9) and (10) in
Section 2.1) this yields,
6 × 10-17
cm2
(Miralda-Escudé
2000).
The redshift factor in the cross-section then cancels exactly the
redshift evolution of the gas density and the resulting optical depth
depends only on the elapsed cosmic time,
t(zreion) - t(zs). At high
redshifts (equations (9) and (10) in
Section 2.1) this yields,
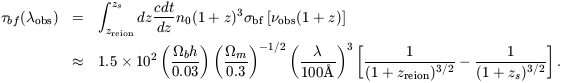
| (116) |
The bound-free optical depth only becomes of order unity in the
extreme UV to soft X-rays, around
h ~ 0.1 keV, a regime which
is unfortunately difficult to observe due to Galactic absorption
(Miralda-Escudé
2000).
~ 0.1 keV, a regime which
is unfortunately difficult to observe due to Galactic absorption
(Miralda-Escudé
2000).
A sketch of the overall spectrum of a source slightly above the
reionization redshift, i.e., with
1 < [(1 + zs) / (1 + zreion)] < 1.18,
is shown in Figure 40. The transmitted flux
between the Gunn-Peterson troughs due to
Ly and
Ly
and
Ly absorption is
suppressed by the Ly
absorption is
suppressed by the Ly forest
in the post-reionization epoch. Transmission of flux due to H II bubbles in the
pre-reionization epoch is expected to be negligible
(Miralda-Escudé
1998).
The redshift of reionization can be inferred in principle from
the spectral shape of the red damping wing
(Miralda-Escudé
& Rees 1998;
Miralda-Escudé 1998)
or from the transmitted flux between the
Lyman series lines
(Haiman & Loeb
1999a).
However, these signatures are complicated in reality by damped
Ly
forest
in the post-reionization epoch. Transmission of flux due to H II bubbles in the
pre-reionization epoch is expected to be negligible
(Miralda-Escudé
1998).
The redshift of reionization can be inferred in principle from
the spectral shape of the red damping wing
(Miralda-Escudé
& Rees 1998;
Miralda-Escudé 1998)
or from the transmitted flux between the
Lyman series lines
(Haiman & Loeb
1999a).
However, these signatures are complicated in reality by damped
Ly systems along the
line of sight or by the inhomogeneity or peculiar velocity field of
the IGM in the vicinity of the source. Moreover, bright sources, such
as quasars, tend to ionize their surrounding environment
(Wood & Loeb 2000)
and the resulting H II region in the IGM could shift the
Ly
systems along the
line of sight or by the inhomogeneity or peculiar velocity field of
the IGM in the vicinity of the source. Moreover, bright sources, such
as quasars, tend to ionize their surrounding environment
(Wood & Loeb 2000)
and the resulting H II region in the IGM could shift the
Ly trough substantially
(Cen & Haiman 2000;
Madau & Rees 2000).
trough substantially
(Cen & Haiman 2000;
Madau & Rees 2000).
The inference of the Ly transmission properties of the IGM from the
observed spectrum of high-redshift sources suffers from uncertainties
about the precise emission spectrum of these sources, and in
particular the shape of their
Ly
transmission properties of the IGM from the
observed spectrum of high-redshift sources suffers from uncertainties
about the precise emission spectrum of these sources, and in
particular the shape of their
Ly emission line. The first
galaxies and quasars are expected to have pronounced recombination lines of
hydrogen and helium due to the lack of dust in their interstellar
medium (see Section 4.1.3 for more
details). Lines such as
H
emission line. The first
galaxies and quasars are expected to have pronounced recombination lines of
hydrogen and helium due to the lack of dust in their interstellar
medium (see Section 4.1.3 for more
details). Lines such as
H or the
He II 1640Å line should reach the
observer unaffected by the intervening IGM, since their wavelength is
longer than that of the Ly
or the
He II 1640Å line should reach the
observer unaffected by the intervening IGM, since their wavelength is
longer than that of the Ly transition which dominates the IGM opacity
(Oh 1999).
However, as described above, the situation is
different for the Ly
transition which dominates the IGM opacity
(Oh 1999).
However, as described above, the situation is
different for the Ly line
photons from the source. As long as
zs > zreion, the intervening
neutral IGM acts like a fog and obscures
the view of the Ly
line
photons from the source. As long as
zs > zreion, the intervening
neutral IGM acts like a fog and obscures
the view of the Ly line
itself [in contrast to the situation with sources at
zs < zreion, where most of the
intervening IGM is ionized and only photons more energetic than
Ly
line
itself [in contrast to the situation with sources at
zs < zreion, where most of the
intervening IGM is ionized and only photons more energetic than
Ly are suppressed by the
Ly
are suppressed by the
Ly forest (see Figure 3)]. Photons which
are emitted at the
Ly
forest (see Figure 3)]. Photons which
are emitted at the
Ly line center have an
initial scattering optical depth of ~ 105 in the surrounding
medium.
line center have an
initial scattering optical depth of ~ 105 in the surrounding
medium.
The Ly line photons are not
destroyed but instead are absorbed
and re-emitted (11) .
Due to the Hubble expansion of the IGM around the
source, the frequency of the photons is slightly shifted by the
Doppler effect in each scattering event. As a result, the photons
diffuse in frequency to the red side of the
Ly
line photons are not
destroyed but instead are absorbed
and re-emitted (11) .
Due to the Hubble expansion of the IGM around the
source, the frequency of the photons is slightly shifted by the
Doppler effect in each scattering event. As a result, the photons
diffuse in frequency to the red side of the
Ly resonance.
Eventually, when their net frequency redshift is sufficiently large,
they escape and travel freely towards the observer (see
Figure 41). As a result, the source creates a faint
Ly
resonance.
Eventually, when their net frequency redshift is sufficiently large,
they escape and travel freely towards the observer (see
Figure 41). As a result, the source creates a faint
Ly halo on the
sky
(12) .
The well-defined radiative transfer problem of a point source of
Ly
halo on the
sky
(12) .
The well-defined radiative transfer problem of a point source of
Ly photons embedded
in a uniform, expanding neutral IGM was solved by
Loeb & Rybicki
(1999).
The Ly
photons embedded
in a uniform, expanding neutral IGM was solved by
Loeb & Rybicki
(1999).
The Ly halo can be simply
characterized by the frequency redshift relative to the line center,
(
halo can be simply
characterized by the frequency redshift relative to the line center,
( -
-

 ), which is
required in order to make the optical depth from the source
[equation (110] equal to unity. At high redshifts, the
leading term in equation (110) yields
), which is
required in order to make the optical depth from the source
[equation (110] equal to unity. At high redshifts, the
leading term in equation (110) yields
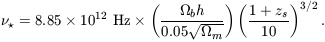
| (117) |
This is the frequency interval over which the damping wing affects the
source spectrum. A frequency shift of
 * = 8.85
× 1012
Hz relative to the line center corresponds to a fractional shift of
(
* = 8.85
× 1012
Hz relative to the line center corresponds to a fractional shift of
( * /
* /

 ) = (v/c) =
3.6 × 10-3 or a Doppler velocity
of v ~ 103 km s-1. The halo size
is then defined by the
corresponding proper distance from the source at which the Hubble
velocity provides a Doppler shift of this magnitude,
) = (v/c) =
3.6 × 10-3 or a Doppler velocity
of v ~ 103 km s-1. The halo size
is then defined by the
corresponding proper distance from the source at which the Hubble
velocity provides a Doppler shift of this magnitude,
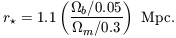
| (118) |
Typically, the Ly halo of a
source at zs ~ 10 occupies an
angular radius of ~ 15" on the sky and yields an
asymmetric line profile as shown in Figures 41 and
42. The scattered photons are highly polarized
and so the shape of the halo would be different if viewed through a
polarization filter
(Rybicki & Loeb
1999).
halo of a
source at zs ~ 10 occupies an
angular radius of ~ 15" on the sky and yields an
asymmetric line profile as shown in Figures 41 and
42. The scattered photons are highly polarized
and so the shape of the halo would be different if viewed through a
polarization filter
(Rybicki & Loeb
1999).
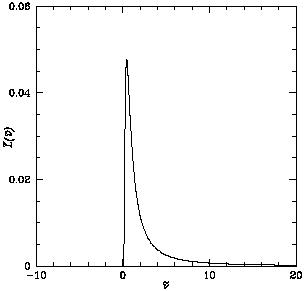
|
Figure 42.
Monochromatic photon luminosity of a
Ly |
Detection of the diffuse Ly halos around bright high-redshift
sources (which are sufficiently rare so that their halos do not
overlap) would provide a unique tool for probing the distribution and
the velocity field of the neutral intergalactic medium before the
epoch of reionization. The Ly
halos around bright high-redshift
sources (which are sufficiently rare so that their halos do not
overlap) would provide a unique tool for probing the distribution and
the velocity field of the neutral intergalactic medium before the
epoch of reionization. The Ly sources serve as lamp posts which
illuminate the surrounding H1 fog. On sufficiently large
scales where the Hubble flow is smooth and the gas is neutral, the
Ly
sources serve as lamp posts which
illuminate the surrounding H1 fog. On sufficiently large
scales where the Hubble flow is smooth and the gas is neutral, the
Ly brightness distribution
can be used to determine the
cosmological mass densities of baryons and matter. Due to their low
surface brightness, the detection of
Ly
brightness distribution
can be used to determine the
cosmological mass densities of baryons and matter. Due to their low
surface brightness, the detection of
Ly halos through a narrow-band
filter is much more challenging than direct observation of their
sources at somewhat longer wavelengths. However, NGST might be able
to detect the Ly
halos through a narrow-band
filter is much more challenging than direct observation of their
sources at somewhat longer wavelengths. However, NGST might be able
to detect the Ly halos
around sources as bright as the quasar discovered by
Fan et al. (2000)
at z = 5.8 or the galaxy discovered by
Hu et al. (1999)
at z = 5.74, even if these sources were moved out to
z ~ 10 (see Section 4 in
Loeb & Rybicki 1999).
The disappearance of
Ly
halos
around sources as bright as the quasar discovered by
Fan et al. (2000)
at z = 5.8 or the galaxy discovered by
Hu et al. (1999)
at z = 5.74, even if these sources were moved out to
z ~ 10 (see Section 4 in
Loeb & Rybicki 1999).
The disappearance of
Ly halos below a certain
redshift can be used to determine zreion.
halos below a certain
redshift can be used to determine zreion.
9.1.2. 21 cm Tomography of the Reionization Epoch
The ground state of hydrogen exhibits hyperfine splitting involving the spins of the proton and the electron. The state with parallel spins (the triplet state) has a slightly higher energy than the state with anti-parallel spins (the singlet state). The 21 cm line associated with the spin-flip transition from the triplet to the singlet state is often used to detect neutral hydrogen in the local universe. At high redshift, the occurrence of a neutral pre-reionization IGM offers the prospect of detecting the first sources of radiation and probing the reionization era by mapping the 21 cm emission from neutral regions. While its energy density is estimated to be only a 1% correction to that of the CMB, the redshifted 21 cm emission should display angular structure as well as frequency structure due to inhomogeneities in the gas density field (Hogan & Rees 1979; Scott & Rees 1990), hydrogen ionized fraction, and spin temperature (Madau, Meiksin, & Rees 1997). Some of the resulting signatures during the pre-overlap phase of reionization (Section 6.3.1) and during the overlap phase are discussed by Tozzi et al. (2000) and Shaver et al. (1999), respectively. Also, the 21 cm signatures have been explored in a numerical simulation by Gnedin & Ostriker (1997). Indeed, a full mapping of the distribution of H1 as a function of redshift is possible in principle. Although detecting the presence of the largest H II regions may be within the reach of proposed instruments such as the Square Kilometer Array (hereafter SKA; see Taylor & Braun 1999), these instruments may not have sufficient sensitivity at the sub-arcminute resolution that would be necessary for a detailed mapping. Moreover, serious technical challenges and problems due to foreground contamination must be overcome even for an initial detection of the reionization signal.
The basic physics of the hydrogen spin transition is determined as follows (for a more detailed treatment, see Madau et al. 1997). The ground-state hyperfine levels of hydrogen tend to thermalize with the CMB background, making the IGM unobservable. If other processes shift the hyperfine level populations away from thermal equilibrium, then the gas becomes observable against the CMB in emission or in absorption. The relative occupancy of the spin levels is usually described in terms of the hydrogen spin temperature TS, defined by
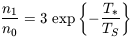
| (119) |
where n0 and n1 are the
singlet and triplet hyperfine levels in the atomic ground state (n = 1),
and T* = 0.07 K is defined by
kB T* = E21, where
the energy of the 21 cm transition is
E21 = 5.9 × 10-6 eV, corresponding to a
frequency of 1420 MHz. In the presence of the CMB alone, the spin states
reach thermal equilibrium with
TS = TCMB = 2.73(1 + z) K on a
time-scale of
T* / (TCMBA10)
 3 × 105(1 +
z)-1 yr,
where A10 = 2.9 × 10-15 s-1 is
the spontaneous decay rate
of the hyperfine transition. This time-scale is much shorter than the age of
the universe at all redshifts after cosmological recombination.
3 × 105(1 +
z)-1 yr,
where A10 = 2.9 × 10-15 s-1 is
the spontaneous decay rate
of the hyperfine transition. This time-scale is much shorter than the age of
the universe at all redshifts after cosmological recombination.
The IGM is observable when the kinetic temperature TK
of the gas differs
from TCMB and an effective mechanism couples
TS to TK. Although collisional
de-excitation of the triplet level
(Purcell & Field
1956)
is a possible mechanism, in the low-density IGM the dominant
mechanism is scattering by
Ly photons
(Wouthuysen 1952;
Field 1958).
Continuum UV photons produced by early radiation sources redshift by
the Hubble expansion into the local
Ly
photons
(Wouthuysen 1952;
Field 1958).
Continuum UV photons produced by early radiation sources redshift by
the Hubble expansion into the local
Ly line at a lower
redshift. These photons mix the spin states via the Wouthuysen-Field
process whereby an atom initially in the n = 1 state absorbs a
Ly
line at a lower
redshift. These photons mix the spin states via the Wouthuysen-Field
process whereby an atom initially in the n = 1 state absorbs a
Ly photon, and the spontaneous decay which returns it from n = 2 to
n = 1 can
result in a final spin state which is different from the initial one. Since
the neutral IGM is highly opaque to resonant scattering, the shape of the
radiation spectrum near Ly
photon, and the spontaneous decay which returns it from n = 2 to
n = 1 can
result in a final spin state which is different from the initial one. Since
the neutral IGM is highly opaque to resonant scattering, the shape of the
radiation spectrum near Ly is determined by TK
(Field 1959),
and the spin temperature is then a weighed mean of TK and
TCMB:
is determined by TK
(Field 1959),
and the spin temperature is then a weighed mean of TK and
TCMB:
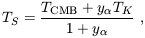
| (120) |
where (if TS >> T*) the
Ly pumping efficiency is
pumping efficiency is
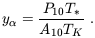
| (121) |
Here P10 is the indirect
de-excitation rate of the triplet n = 1 state via the Wouthuysen-Field
process, related to the total scattering rate
P of
Ly
of
Ly photons by P10 =
4P
photons by P10 =
4P / 27
(Field 1958).
Thus the critical value
of P
/ 27
(Field 1958).
Thus the critical value
of P is given
by the thermalization rate
(Madau et al. 1997)
is given
by the thermalization rate
(Madau et al. 1997)
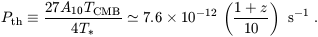
| (122) |
A patch of neutral hydrogen at the mean density and with a uniform TS produces an optical depth at 21(1 + z) cm of
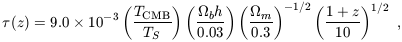
| (123) |
assuming a high redshift
z. Since the brightness temperature through the IGM is
Tb = TCMB
e- +
TS (1 -
e-
+
TS (1 -
e- ), the
observed differential antenna temperature of this region relative to the CMB is
(Madau et al. 1997,
with the
), the
observed differential antenna temperature of this region relative to the CMB is
(Madau et al. 1997,
with the  m
dependence added)
m
dependence added)
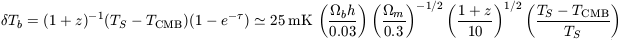
| (124) |
where  << 1 is assumed and
<< 1 is assumed and
 Tb has
been redshifted to redshift zero. In overdense regions, the observed
Tb has
been redshifted to redshift zero. In overdense regions, the observed
 Tb is
proportional to the overdensity, and in partially ionized regions
Tb is
proportional to the overdensity, and in partially ionized regions
 Tb is
proportional to the neutral fraction. Thus, if
TS >> TCMB then
the IGM is observed in emission at a level that is independent of
TS. On the other hand, if
TS << TCMB then the IGM is observed in
absorption at a level that is a factor
~ TCMB / TS larger than
in emission. As a result, a number of cosmic events are expected to leave
observable signatures in the redshifted 21 cm line.
Tb is
proportional to the neutral fraction. Thus, if
TS >> TCMB then
the IGM is observed in emission at a level that is independent of
TS. On the other hand, if
TS << TCMB then the IGM is observed in
absorption at a level that is a factor
~ TCMB / TS larger than
in emission. As a result, a number of cosmic events are expected to leave
observable signatures in the redshifted 21 cm line.
Since the CMB temperature is only 2.73(1 + z) K, even relatively
inefficient heating mechanisms are expected to heat the IGM above
TCMB well before reionization. Possible preheating
sources include soft
X-rays from early quasars or star-forming regions, as well as thermal
bremsstrahlung from ionized gas in collapsing halos. However, even the
radiation from the first stars may suffice for an early preheating. Only
~ 10% of the present-day global star formation rate is required
(Madau et al. 1997)
for a sufficiently strong
Ly background which
produces a scattering rate above the thermalization rate
Pth. Such
a background drives TS to the kinetic gas temperature,
which is initially lower than
TCMB because of adiabatic expansion. Thus,
the entire IGM can be seen in absorption, but the IGM is then heated above
TCMB in ~ 108 yr
(Madau et al. 1997)
by the atomic recoil
in the repeated resonant Ly
background which
produces a scattering rate above the thermalization rate
Pth. Such
a background drives TS to the kinetic gas temperature,
which is initially lower than
TCMB because of adiabatic expansion. Thus,
the entire IGM can be seen in absorption, but the IGM is then heated above
TCMB in ~ 108 yr
(Madau et al. 1997)
by the atomic recoil
in the repeated resonant Ly scattering. According to Section 8.1 (also
compare
Gnedin 2000a),
the required level of star
formation is expected to be reached already at z ~ 20, with the entire
IGM heated well above the CMB by the time overlap begins at z ~
10. Thus, although the initial absorption signal is in principle
detectable with the SKA
(Tozzi et al. 2000),
it likely occurs at
scattering. According to Section 8.1 (also
compare
Gnedin 2000a),
the required level of star
formation is expected to be reached already at z ~ 20, with the entire
IGM heated well above the CMB by the time overlap begins at z ~
10. Thus, although the initial absorption signal is in principle
detectable with the SKA
(Tozzi et al. 2000),
it likely occurs at
 100
MHz where Earth-based radio interference is highly problematic.
100
MHz where Earth-based radio interference is highly problematic.
As individual ionizing sources turn on in the pre-overlap stage of reionization, the resulting H II bubbles may be individually detectable if they are produced by rare and luminous sources such as quasars. If the H II region expands into an otherwise unperturbed IGM, then the expanding shell can be mapped as follows (Tozzi et al. 2000). The H II region itself, of course, shows neither emission nor absorption. Outside the ionized bubble, a thin shell of neutral gas is heated above the CMB temperature and shows up in emission. A much thicker outer shell is cooler than the CMB due to adiabatic expansion, but satisfies TS = TK and produces absorption. Finally, at large distances from the quasar, TS approaches TCMB as the quasar radiation weakens. For a quasar with an ionizing intensity of 1057 photons s-1 observed after ~ 107 yr with 2' resolution and 1 MHz bandwidth, the signal ranges from -3 to 3 µJy per beam (Tozzi et al. 2000). Mapping such regions would convey information on the quasar number density, ionizing intensity, opening angle, and on the density distribution in the surrounding IGM. Note, however, that an H II region which forms at a redshift approaching overlap expands into a preheated IGM. In this case, the H II region itself still appears as a hole in an otherwise emitting medium, but the quasar-induced heating is not probed, and there is no surrounding region of absorption to supply an enhanced contrast.
At redshifts approaching overlap, the IGM should be almost entirely
neutral but with
TS >> TCMB. In this redshift range there
should still be an interesting signal due to density fluctuations. The
same cosmic network of sheets and filaments that gives rise to the
Ly forest observed at
z
forest observed at
z  5 should
lead to fluctuations in
the 21 cm brightness temperature at higher redshifts. At 150 MHz
(z = 8.5), for observations with a bandwidth of 1 MHz, the root mean
square fluctuation should be ~ 10 mK at 1', decreasing with scale
(Tozzi et al. 2000).
5 should
lead to fluctuations in
the 21 cm brightness temperature at higher redshifts. At 150 MHz
(z = 8.5), for observations with a bandwidth of 1 MHz, the root mean
square fluctuation should be ~ 10 mK at 1', decreasing with scale
(Tozzi et al. 2000).
A further signature, observable over the entire sky, should mark the overlap stage of reionization. During overlap, the IGM is transformed from being a neutral, preheated and thus emitting gas, to being almost completely ionized. This disappearance of the emission over a relatively narrow redshift range can be observed as a drop in the brightness temperature at the frequencies corresponding to the latter stages of overlap (Shaver et al. 1999). This exciting possibility, along with those mentioned above, face serious challenges in terms of signal contamination and calibration. The noise sources include galactic and extragalactic emission sources, as well as terrestrial interference, and all of these foregrounds must be modeled and accurately removed in order to observe the fainter cosmological signal (see Shaver et al. 1999 for a detailed discussion). For the overlap stage in particular, the sharpness of the spectral feature is the key to its detectability, but it may be significantly smoothed by inhomogeneities in the IGM.
9.2. Effect of Reionization on CMB Anisotropies
In standard cosmological models, the early universe was hot and permeated by a nearly uniform radiation bath. At z ~ 1200 the free protons and electrons recombined to form hydrogen atoms, and most of the photons last scattered as the scattering cross-section dropped precipitously. These photons, observed today as the Cosmic Microwave Background (CMB), thus yield a snapshot of the state of the universe at that early time. Small fluctuations in the density, velocity, and gravitational potential lead to observed anisotropies (e.g., Bennett et al. 1996) that can be analyzed to yield a great wealth of information on the matter content of the universe and on the values of the cosmological parameters (e.g., Hu 1995; Jungman et al. 1996).
Reionization can alter the anisotropy spectrum, by erasing some of the primary anisotropy imprinted at recombination, and by generating additional secondary fluctuations that could be used to probe the era of reionization itself (see Haiman & Knox 1999 for a review). The primary anisotropy is damped since the rescattering leads to a blending of photons from initially different lines of sight. Furthermore, not all the photons scatter at the same time, rather the last scattering surface has a finite thickness. Perturbations on scales smaller than this thickness are damped since photons scattering across many wavelengths give canceling redshifts and blueshifts. If reionization occurs very early, the high electron density produces efficient scattering, and perturbations are damped on all angular scales except for the very largest.
The optical depth to scattering over a proper length dl is
d =
=
 T
ne dl, where
T
ne dl, where
 T is the Thomson
cross-section
and ne the density of free electrons. If reionization occurs
instantaneously at redshift z, then the total scattering optical
depth in
T is the Thomson
cross-section
and ne the density of free electrons. If reionization occurs
instantaneously at redshift z, then the total scattering optical
depth in  CDM is given by
(e.g., Section 7.1.1 of
Hu 1995)
CDM is given by
(e.g., Section 7.1.1 of
Hu 1995)
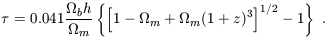
| (125) |
With our standard parameters (end
of Section 1) this implies
 = 0.037 at the current lower limit
on reionization of z = 5.8
(Fan et al. 2000),
with
= 0.037 at the current lower limit
on reionization of z = 5.8
(Fan et al. 2000),
with  = 0.10 if
z = 11.6 and
= 0.10 if
z = 11.6 and  = 0.15 if
z = 15.3. Recent observations of small-scale anisotropies
(Lange et al. 2000;
Balbi et al. 2000)
revealed a peak in the power spectrum on a ~ 1° scale, as
expected from the primary anisotropies in standard cosmological
models. This indicates that the reionization damping, if present, is
not very large, and the observations set a limit of
= 0.15 if
z = 15.3. Recent observations of small-scale anisotropies
(Lange et al. 2000;
Balbi et al. 2000)
revealed a peak in the power spectrum on a ~ 1° scale, as
expected from the primary anisotropies in standard cosmological
models. This indicates that the reionization damping, if present, is
not very large, and the observations set a limit of
 < 0.33 at 95% confidence
(Tegmark &
Zaldarriaga 2000)
and, therefore, imply
that reionization must have occurred at z
< 0.33 at 95% confidence
(Tegmark &
Zaldarriaga 2000)
and, therefore, imply
that reionization must have occurred at z
 30.
30.
However, measuring a small  from
the temperature anisotropies
alone is expected to be very difficult since the anisotropy spectrum
depends on a large number of other parameters, creating a
near-degeneracy which limits our ability to measure each parameter
separately; the degeneracy of tau with other cosmological parameters
is due primarily to a degeneracy with the gravitational-wave
background. However, Thomson scattering also creates net polarization
for incident radiation which has a quadrupole anisotropy. This
anisotropy was significant at reionization due to large-scale
structure which had already affected the gas distribution. The result
is a peak in the polarization power spectrum on large angular scales
of order tens of degrees
(Zaldarriaga 1997).
Although experiments must
overcome systematic errors from the detector itself and from polarized
foregrounds (such as galactic dust emission and synchrotron
radiation), parameter estimation models
(Eisenstein, Hu, &
Tegmark 1999;
Zaldarriaga, Spergel,
& Seljak 1997)
suggest that the peak can
be used to measure even very small values of
from
the temperature anisotropies
alone is expected to be very difficult since the anisotropy spectrum
depends on a large number of other parameters, creating a
near-degeneracy which limits our ability to measure each parameter
separately; the degeneracy of tau with other cosmological parameters
is due primarily to a degeneracy with the gravitational-wave
background. However, Thomson scattering also creates net polarization
for incident radiation which has a quadrupole anisotropy. This
anisotropy was significant at reionization due to large-scale
structure which had already affected the gas distribution. The result
is a peak in the polarization power spectrum on large angular scales
of order tens of degrees
(Zaldarriaga 1997).
Although experiments must
overcome systematic errors from the detector itself and from polarized
foregrounds (such as galactic dust emission and synchrotron
radiation), parameter estimation models
(Eisenstein, Hu, &
Tegmark 1999;
Zaldarriaga, Spergel,
& Seljak 1997)
suggest that the peak can
be used to measure even very small values of
 : 2% for the
upcoming MAP satellite, and 0.5% for the Planck satellite which
will reach smaller angular scales with higher accuracy.
: 2% for the
upcoming MAP satellite, and 0.5% for the Planck satellite which
will reach smaller angular scales with higher accuracy.
Reionization should also produce additional temperature anisotropies on small scales. These result from the Doppler effect. By the time of reionization, the baryons have begun to follow dark matter potentials and have acquired a bulk velocity. Since the electrons move with respect to the radiation background, photons are given a Doppler kick when they scatter off the electrons. Sunyaev (1978) and Kaiser (1984) showed, however, that a severe cancellation occurs if the electron density is homogeneous. Opposite Doppler shifts on crests and troughs of a velocity perturbation combine to suppress the anisotropy induced by small-scale velocity perturbations. The cancellation is made more severe by the irrotational nature of gravitationally-induced flows. However, if the electron density varies spatially, then the scattering probability is not equal on the crest and on the trough, and the two do not completely cancel. Since a non-zero effect requires variation in both electron density and velocity, it is referred to as a second-order anisotropy.
The electron density can vary due to a spatial variation in either the baryon density or the ionized fraction. The former is referred to as the Ostriker-Vishniac effect (Ostriker & Vishniac 1986; Vishniac 1987). The latter depends on the inhomogeneous topology of reionization, in particular on the size of H II regions due to individual sources (Section 6.2) and on spatial correlations among different regions. Simple models have been used to investigate the character of anisotropies generated during reionization (Gruzinov & Hu 1998; Knox et al. 1998; Aghanim et al. 1996). The Ostriker-Vishniac effect is expected to dominate all anisotropies at small angular scales (e.g., Jaffe & Kamionkowski 1998), below a tenth of a degree, because the primary anisotropies are damped on such small scales by diffusion (Silk damping) and by the finite thickness of the last scattering surface. Anisotropies generated by inhomogeneous reionization may be comparable to the Ostriker-Vishniac effect, and could be detected by MAP and Planck, if reionization is caused by bright quasars with 10 Mpc-size ionized bubbles. However, the smaller bubbles expected for mini-quasars or for star-forming dwarf galaxies would produce an anisotropy signal which is weaker and at smaller angular scales, likely outside the range of the upcoming satellites (see, e.g., Haiman & Knox 1999 for discussion). Gnedin & Jaffe (2000) used a numerical simulation to show that, in the case of stellar reionization, the effect on the CMB of patchy reionization is indeed sub-dominant compared to the contribution of non-linear density and velocity fluctuations. Nevertheless, a signature of reionization could still be detected in future measurements of CMB angular fluctuations on the scale of a few arcseconds (see also Bruscoli et al. 2000, who find a somewhat higher power spectrum due to patchy reionization).
9.3. Remnants of High-Redshift Systems in the Local Universe
At the end of the reionization epoch, the heating of the IGM resulted
in the photo-evaporation of gas out of halos of circular velocity
Vc above ~ 10-15 km s-1
(Section 6.4). The
pressure of the hot gas subsequently shut off gas infall into even
more massive halos, those with
Vc ~ 30 km s-1
(Section 6.5). Thus, the gas reservoir of
photo-evaporating halos
could not be immediately replenished. Some dwarf galaxies which were
prevented from forming after reionization could have eventually
collected gas at z = 1-2, when the UV background flux declined
sufficiently
(Babul & Rees 1992;
Kepner, Babul, &
Spergel 1997).
However,
Kepner et al. (1997)
found that even if the ionizing
intensity J21 declines as (1 + z)4
below z = 3, only halos with
Vc  20 km s-1 can form atomic hydrogen by z
= 1, and
Vc
20 km s-1 can form atomic hydrogen by z
= 1, and
Vc  25 km s-1 is required to form molecular hydrogen.
While the fact that the IGM was reionized has almost certainly
influenced the abundance and properties of dwarf galaxies observed
today, the exact manifestations of this influence and ways to prove
that they occurred have not been well determined. In this section we
summarize recent work on this topic, which should remain an active
research area.
25 km s-1 is required to form molecular hydrogen.
While the fact that the IGM was reionized has almost certainly
influenced the abundance and properties of dwarf galaxies observed
today, the exact manifestations of this influence and ways to prove
that they occurred have not been well determined. In this section we
summarize recent work on this topic, which should remain an active
research area.
The suppression of gas infall mentioned above suggests that the
abundance of luminous halos as a function of circular velocity should
show a break, with a significant drop in the abundance below
Vc = 30I>km s-1. Such a drop may
in fact be required in order to reconcile the
 CDM model with observations.
Klypin et al. (1999) and
Moore et al. (1999)
found that the abundance of halos with
Vc ~ 10-30 km s-1 in
numerical simulations of the
Local Group environment is higher by an order of magnitude than the
observed dwarf galaxy abundance. The predicted and observed abundances
matched well at Vc > 50 km s-1.
Bullock et al. (2000a)
considered whether photoionization can explain the discrepancy at the
low-mass end by preventing dark matter halos from forming stars. They
assumed that a sub-halo in the Local Group can host an observable
galaxy only if already at reionization its main progenitor contained a
fraction f of the final sub-halo mass. Using semi-analytic modeling,
they found a close match to the observed circular velocity
distribution for zreion = 8 and f = 0.3.
CDM model with observations.
Klypin et al. (1999) and
Moore et al. (1999)
found that the abundance of halos with
Vc ~ 10-30 km s-1 in
numerical simulations of the
Local Group environment is higher by an order of magnitude than the
observed dwarf galaxy abundance. The predicted and observed abundances
matched well at Vc > 50 km s-1.
Bullock et al. (2000a)
considered whether photoionization can explain the discrepancy at the
low-mass end by preventing dark matter halos from forming stars. They
assumed that a sub-halo in the Local Group can host an observable
galaxy only if already at reionization its main progenitor contained a
fraction f of the final sub-halo mass. Using semi-analytic modeling,
they found a close match to the observed circular velocity
distribution for zreion = 8 and f = 0.3.
These results neglect several complications. As mentioned above, halos
with Vc  20 km s-1 may be able to accrete gas and
form stars once again at z
20 km s-1 may be able to accrete gas and
form stars once again at z
 1. Any accreted gas
at low redshift
could have been previously enriched with metals and molecules, thus
enabling more efficient cooling. On the other hand, if the progenitors
had a Vc
1. Any accreted gas
at low redshift
could have been previously enriched with metals and molecules, thus
enabling more efficient cooling. On the other hand, if the progenitors
had a Vc  17 km s-1 at
zreion then they were not able
to cool and form stars, unless molecular hydrogen had not been
dissociated (Section 3.3). In order to
reconcile the
photoionization scenario with the recent episodes of star formation
deduced to have occurred in most dwarf galaxies (e.g.,
Mateo 1998;
Grebel 1998),
a continuous recycling of gas over many generations of
stars must be assumed. This would mean that supernova feedback
(Section 7.1) was unable to shut off star
formation even in these
smallest known galaxies. In addition, the existence of a large
abundance of sub-halos may be problematic even if the sub-halos have
no gas, since they would interact with the disk dynamically and tend
to thicken it
(Toth & Ostriker
1992;
Moore et al. 1999;
Velazquez & White
1999).
17 km s-1 at
zreion then they were not able
to cool and form stars, unless molecular hydrogen had not been
dissociated (Section 3.3). In order to
reconcile the
photoionization scenario with the recent episodes of star formation
deduced to have occurred in most dwarf galaxies (e.g.,
Mateo 1998;
Grebel 1998),
a continuous recycling of gas over many generations of
stars must be assumed. This would mean that supernova feedback
(Section 7.1) was unable to shut off star
formation even in these
smallest known galaxies. In addition, the existence of a large
abundance of sub-halos may be problematic even if the sub-halos have
no gas, since they would interact with the disk dynamically and tend
to thicken it
(Toth & Ostriker
1992;
Moore et al. 1999;
Velazquez & White
1999).
However, the photoionization scenario is useful because it may be testable through other implications. For example, Bullock et al. (2000b) used semi-analytic modeling to show that many subhalos which did form stars before reionization were tidally disrupted in the Milky Way's gravitational field, and the resulting stellar streams may be observable. The formation of the Milky Way's stellar component has also been investigated by White & Springel (2000). They combined a scaled-down dark matter cluster simulation with semi-analytic prescriptions for star formation in halos, and showed that the oldest stars in the Milky Way should be located mostly in the inner halo or bulge, but they cannot be easily identified because the populations of old stars and of low metallicity stars are only weakly correlated.
Gnedin (2000c)
pointed out several observed features of dwarf galaxies
that may be related to their high-redshift histories. First, almost
all Local Group dwarf galaxies with measured star formation histories
show a sharp decline in the star formation rate around 10 Gyr ago.
Gnedin noted that this drop could correspond to the suppression of
star formation due to reionization
(Section 6.5) if the measured
ages of the old stellar populations are somewhat underestimated; or
that it could instead correspond to the additional suppression caused
by helium reionization (Section 6.3.2)
at z  3. He showed
that if only the old stellar population is considered, then the
Schmidt Law (Section 5.2) implies that the
luminosity of each
dwarf galaxy, divided by a characteristic volume containing a fixed
fraction of all the old stars, should be proportional to some power of
the central luminosity density. This assumes that the present central
luminosity density of old stars is a good measure of the original gas
density, i.e., that in the core almost all the gas was transformed
into stars, and feedback did not play a role. It also assumes that the
gas density distribution was self-similar in all the dwarf galaxies
during the period when they formed stars, and that the length of this
period was also the same in all galaxies. These assumptions are
required in order for the total stellar content of each galaxy to be
simply related to the central density via the Schmidt Law evaluated at
the center. Taking ten galaxies which have well-measured star
formation histories, and which formed most of their stars more than 10
Gyr ago, Gnedin found a correlation with a power law of 3/2, as
expected from the Schmidt Law (Section 5.2).
Clearly, the
theoretical derivation of this correlation combines many simplistic
assumptions. However, explaining the observed correlation is a
challenge for any competing models, e.g., models where feedback plays
a dominant role in regulating star formation.
3. He showed
that if only the old stellar population is considered, then the
Schmidt Law (Section 5.2) implies that the
luminosity of each
dwarf galaxy, divided by a characteristic volume containing a fixed
fraction of all the old stars, should be proportional to some power of
the central luminosity density. This assumes that the present central
luminosity density of old stars is a good measure of the original gas
density, i.e., that in the core almost all the gas was transformed
into stars, and feedback did not play a role. It also assumes that the
gas density distribution was self-similar in all the dwarf galaxies
during the period when they formed stars, and that the length of this
period was also the same in all galaxies. These assumptions are
required in order for the total stellar content of each galaxy to be
simply related to the central density via the Schmidt Law evaluated at
the center. Taking ten galaxies which have well-measured star
formation histories, and which formed most of their stars more than 10
Gyr ago, Gnedin found a correlation with a power law of 3/2, as
expected from the Schmidt Law (Section 5.2).
Clearly, the
theoretical derivation of this correlation combines many simplistic
assumptions. However, explaining the observed correlation is a
challenge for any competing models, e.g., models where feedback plays
a dominant role in regulating star formation.
Barkana & Loeb (1999)
noted that a particularly acute puzzle is
presented by the very smallest galaxies, the nine dwarf spheroidals in
the Local Group with central velocity dispersions

 10 km
s-1, including five below 7 km
s-1 (see recent reviews by
Mateo 1998 &
van den Bergh 2000).
These galaxies contain
old stars that must have formed at z
10 km
s-1, including five below 7 km
s-1 (see recent reviews by
Mateo 1998 &
van den Bergh 2000).
These galaxies contain
old stars that must have formed at z
 2, before the ionizing
background dropped sufficiently to allow them to form. There are
several possible solutions to the puzzle of how these stars formed in
such small halos or in their progenitors which likely had even smaller
velocity dispersions. The solutions are that (i) molecular hydrogen
allowed these stars to form at
z > zreion, as noted above, (ii) the
measured stellar velocity dispersions of the dwarf galaxies are well
below the velocity dispersions of their dark matter halos, or (iii)
the dwarf galaxies did not form via the usual hierarchical scenario.
2, before the ionizing
background dropped sufficiently to allow them to form. There are
several possible solutions to the puzzle of how these stars formed in
such small halos or in their progenitors which likely had even smaller
velocity dispersions. The solutions are that (i) molecular hydrogen
allowed these stars to form at
z > zreion, as noted above, (ii) the
measured stellar velocity dispersions of the dwarf galaxies are well
below the velocity dispersions of their dark matter halos, or (iii)
the dwarf galaxies did not form via the usual hierarchical scenario.
One major uncertainty in comparing observations to hierarchical models
is the possibility that the measured velocity dispersion of stars in
the dwarf spheroidals underestimates the velocity dispersion of their
dark halos. Assuming that the stars are in equilibrium, their velocity
dispersion could be lower than that of the halo if the mass profile is
shallower than isothermal beyond the stellar core. The velocity
dispersion and mass-to-light ratio of a dwarf spheroidal could also
appear high if the galaxy is non-spherical or the stellar orbits are
anisotropic. The observed properties of dwarf spheroidals require a
central mass density of order
0.1 M pc-3 (e.g.,
Mateo 1998),
which is ~ 7 × 105 times the present critical
density. Thus, only the very inner parts of the halos are sampled by
the central velocity dispersion. Detailed observations of the velocity
dispersion profiles of these galaxies could be used to determine the
circular velocity of the underlying halo more reliably.
pc-3 (e.g.,
Mateo 1998),
which is ~ 7 × 105 times the present critical
density. Thus, only the very inner parts of the halos are sampled by
the central velocity dispersion. Detailed observations of the velocity
dispersion profiles of these galaxies could be used to determine the
circular velocity of the underlying halo more reliably.
A cosmological scenario for the formation of dwarf spheroidal galaxies is favored by the fact that they are observed to be dark matter dominated, but this may not rule out all the alternatives. The dwarf dark halos may have formed at low redshift by the breakup of a much larger galaxy. Under this scenario, gas forming stars inside the large parent galaxy would have been unaffected by the photoionizing background. At low redshift, this galaxy may have collided with the Milky Way or come close enough to be torn apart, forming at least some of the dwarf spheroidal systems. Simulations of galaxy encounters (Barnes & Hernquist 1992; Elmegreen, Kaufman, & Thomasson 1993) have found that shocks in the tidal tails trigger star formation and lead to the formation of dwarf galaxies, but these galaxies contain only small amounts of dark matter. However, the initial conditions of these simulations assumed parent galaxies with a smooth dark matter distribution rather than clumpy halos with dense sub-halos inside them. As noted above, simulations (Klypin et al. 1999; Moore et al. 1999) suggest that galaxy halos may have large numbers of dark matter satellites, and further simulations are needed to test whether these subhalos can capture stars which form naturally in tidal tails.
A common origin for the Milky Way's dwarf satellites (and a number of halo globular clusters), as remnants of larger galaxies accreted by the Milky Way galaxy, has been suggested on independent grounds. These satellites appear to lie along two (e.g., Majewski 1994) or more (Lynden-Bell & Lynden-Bell 1995, Fusi-Pecci et al. 1995) polar great circles. The star formation history of the dwarf galaxies (e.g., Grebel 1998) constrains their merger history, and implies that the fragmentation responsible for their appearance must have occurred early in order to be consistent with the variation in stellar populations among the supposed fragments (Unavane, Wyse, & Gilmore 1996; Olszewski 1998). Observations of interacting galaxies (outside the Local Group) also demonstrate that ``tidal dwarf galaxies'' do indeed form (e.g., Duc & Mirabel 1997; Hunsberger, Charlton, & Zaritsky 1996).
10 We define the reionization redshift to be the redshift at which the individual H II regions overlapped and most of the IGM volume was ionized. In most realistic scenarios, this transition occurs rapidly on a time-scale much shorter than the age of the universe (see Section 6.3.1). This is mainly due to the short distances between neighboring sources. Back.
11 At the redshifts of interest,
zs ~ 10,
the low densities and lack of chemical enrichment of the IGM make the
destruction of Ly photons by
two-photon decay or dust absorption unimportant.
Back.
photons by
two-photon decay or dust absorption unimportant.
Back.
12 The photons absorbed in the
Gunn-Peterson trough are also re-emitted by the IGM around the
source. However, since these photons originate on the blue side of the
Ly resonance, they travel a
longer distance from the source,
compared to the Ly
resonance, they travel a
longer distance from the source,
compared to the Ly line
photons, before they escape to the
observer. The Gunn-Peterson photons are therefore scattered from a
larger and hence dimmer halo around the source. The Gunn-Peterson
halo is made even dimmer relative to the
Ly
line
photons, before they escape to the
observer. The Gunn-Peterson photons are therefore scattered from a
larger and hence dimmer halo around the source. The Gunn-Peterson
halo is made even dimmer relative to the
Ly line halo by the fact
that the luminosity of the source per unit frequency is often much
lower in the continuum than in the
Ly
line halo by the fact
that the luminosity of the source per unit frequency is often much
lower in the continuum than in the
Ly line.
Back.
line.
Back.