5.2. Formation of pancakes from primeval adiabatic perturbations

In Section 4, we discussed the damping of adiabatic fluctuations prior to and during recombination, with the result that linear adiabatic ftuctuations are damped on mass scales M_D [Eq. (4.12)]. Since the density fluctuations are assumed to be everywhere small, the linear theory results of Section 5.1 may be used to discuss the early phase of gravitational instability.

From Eq. (5.7) we see that in linear theory, the peculiar velocity at any point q may be written as a separable function of the variables (q, t). On keeping just the dominant mode we have,

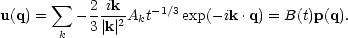(5.17)

Integrating (5.17), it follows that the coordinate x of a fluid element may be written,

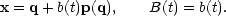(5.18)

The coordinates q are taken to define the unperturbed background and term b(t)p(q) represents the initial irregularity in the matter distribution, assumed to be small. Equations (5.17) and (5.18) are expected to be an accurate approximation while perturbations are in the linear regime, but Zel'dovich (1970) has pointed out that they may also be used as a guide to the evolution of irregularities when / >> 1. Consider the density of a fixed fluid element in the neighbourhood of x at t_i. The density at a later time t is given by the Jacobian of the transformation between the coordinate systems (x, q), thus

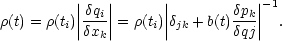(5.19)

Evaluating the Jacobian to first order,

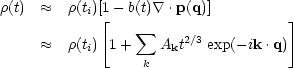(5.20)

in agreement with linear theory, Eq. (5.7a). By extrapolating the result of (5.19), infinite density is achieved at some time t when the determinant in (5.19) vanishes. Thus the matter will in general pile up into sheets (pancakes) along the surfaces defined by the condition |x_k / q_j| = 0. This is illustrated in Figure 5.1 where we compare the Zel'dovich approximate theory with a three-dimensional N-body simulation (Davis, Efstathiou, Frenk and White, in preparation). Here a particle is initially placed at the centre of each of 32³ cells of a three dimensional lattice. The particle coordinates q_i are then displaced by a small amount p(q_i) evaluated from (5.17) with A_k = const × exp(- ik _k) for k_i < k_D and A_k = 0 for k_i > k_D where _D = 2 / k_D = 0.5 times the length of the periodic box. The cosmological density parameter was set to = 1 and the amplitude of the initial perturbations was adjusted so that pancakes would form when the system had expanded by a factor of 4.5. The pictures in the left-hand panel of Figure 5.1 show an N-body simulation in which forces were calculated using a Fast Fourier transform potential solver on a 64³ grid (see e.g. Efstathiou and Eastwood 1981 and references therein). The pictures in the right hand panel show the same initial conditions evolved using the Zel'dovich approximation Eq. (5.18). The Zel'dovich approximation compares very well with the N-body simulation, especially at early times. At late times, after the "caustics" have formed, the Zel'dovich approximation fails to reproduce the dense knots which develop at the intersection of sheets and filaments. In Figure 5.2 we show three projections of the particle positions in the N-body simulation after expansion by a factor of 8.2. The dominant visual impression is of long filaments, but careful inspection reveals sheet-like structures as well. By the time the system has expanded by a factor ~ 12, there remain only weak remnants of filamentary and sheet-like structures.

Figure 5.1. Comparison of the Zel'dovich approximation Eq. (5.18) with a numerical simulation of gravitational clustering using "pancake" initial conditions. The three rows show projections of the particle positions after the system had expanded by factors of 2.4, 3.6 and 5.4 respectively. Pictures to the left show the N-body simulation and pictures to the right show the Zel'dovich approximation

Figure 5.2. Three projections of the numerical simulation shown in Figure 5.1 after the system had expanded by a factor of 8.2.

Two-dimensional simulations which include gravity have been done by Doroshkevich et al. (1980a) and by Melott (1983). Three-dimensional simulations have been presented by Klypin and Shandarin (1983) and by Frenk, White and Davis (1983).

These results show that if we have primordial adiabatic fluctuation (and no significant contribution to the mass density from "exotic" weakly interacting particles with masses >> 1 keV - see Sections 9.3 and 10) the first objects to fragment out of the background will be "pancakes" or prolate structures with linear dimensions ~ 2 / k_D. However, since it is assumed that / is everywhere small initially, the matter will still be gaseous at the time of collapse and hence a shock will form as fluid elements intersect with high relative velocity. Now from Eq. (4.12) the characteristic damping mass scale is M_D 1.3 × 10¹²( h²)^-3/2 M and is, therefore, much larger than a typical galactic mass (10¹¹ M) if < 1. In this case, galaxy formation must proceed by the fragmentation of the pancakes. Some aspects of the fragmentation process will be discussed in Section 8.

A similar scenario results if the mean-mass density of the universe is dominated by massive neutrinos. In this case, fluctuations in the neutrino density are erased on mass scales smaller than

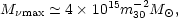(5.21)

where m₃₀ is the neutrino mass in units of 30 eV (Bond, Efstathiou and Silk, 1980). The damping is due to a combination of directional dispersion while the neutrinos are relativistic and a type of Landau damping when they are non-relativistic (this is discussed in more detail in section 9). Detailed numerical calculations of the damping of neutrino fluctuations have been presented by Peebles (1982a) and Bond and Szalay (1983). In this picture, baryons will collapse together with the neutrinos into pancakes of mass ~ M_max and the luminous parts of galaxies must form by the fragmentation of the shocked gas. It has been argued (e.g. Peebles, 1974a; Fall, 1980a) that these theories for the formation of galaxies and clusters might be inconsistent with the observed power-law slope of the two-point correlation function (r) (Eq. 2.27) since the fluctuation spectra possess a preferred scale. However, the numerical simulations of Frenk et al. and Klypin and Shandarin produce power-law correlation functions. The slope of the two-point function varies with time, but there is a unique epoch at which the models yield a power law (r) r^-1.8 in agreement with observations [cf. Eq. (2.27)]. [We have done similar numerical simulations to those of Frenk et al. and find that at late times, when the clustering is highly non-linear, the models develop a three-point correlation function with a form similar to that of Eq. (2.28)]. It is difficult to judge whether these detailed results provide strong support for pancake theories. As we have remarked above, in these theories galaxies can only form after the dissipative collapse of gas. The small-scale clustering properties of galaxies could be quite different to those inferred from purely dissipationless N-body models. For example, one might expect galaxies to form in predominantly high density regions and one could even envisage gas dynamical effects which could inhibit galaxy formation in very massive pancakes (Bond et al., 1983).

The two-point correlation function may be used to set useful constraints on these theories. The observed lack of clustering on scales > r₀ ~ 5h^-1 Mpc suggests that any fluctuations on larger scales should still be in the linear regime of growth. Consider, for example, the spectrum used in the models shown in Figures 5.1 and 5.2. The two-point correlation function in the linear regime is,

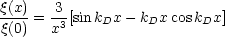(5.22)

where (0) is the amplitude of the correlation function at zero lag. Perturbations will enter the non-linear regime when (0) 1. A measure of the width of (x) is given by

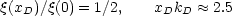(5.23)

(Peebles, 1981a, Peebles, 1982a) and it is reasonable to require r > x_D at the present epoch. The detailed numerical simulations of Frenk et al. suggest that 2r₀ > x_D is a more accurate criterion. Applying this restriction we find the limits

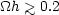(5.24a)

for adiabatic fluctuations with massless neutrinos, and

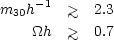(5.24b)

for adiabatic fluctuations with massive neutrinos. A more detailed discussion should properly take into account the dependence of the shape of (x) on the spectral index n; in the massless neutrino case, the broad spectrum (Figure 4.2) implies that n 2 (Peebles, 1981a, Silk, 1982) and the massive neutrino case is discussed in Section 9.2 (also Peebles, 1982a).

The constraints of Eqs. (5.24) agree qualitatively with the limits deduced from the small-scale anisotropies of the microwave background described in Section 4, i.e. the theories are compatible with observational constraints only if h ~ 1. This may be difficult to reconcile with measurements of the cosmological density parameter (Section 2.4) unless the dark material is distributed more uniformly than galaxies on scales < r₀. The observed cosmic abundances of helium and especially deuterium require a low value of the baryon density, _B ~ 0.1 (see Pagel, 1982, for an excellent review). The latter constraint is partly responsible for the current popularity of models with massive neutrinos. In these models it is possible that _T = + _B 1 in order to satisfy the microwave background limits and Eq. (5.24b) whilst _B 0.1 to give agreement with primordial nucleosynthesis (Schramm and Steigman, 1981). Massive neutrinos also offer an excellent alternative to the traditional forms of dark material such as low mass stars.

As the numerical simulations show, it is unlikely that pancake structure would survive to the present epoch unless pancake formation occurred very recently, at redshifts z ~ 1. Even a redshift z ~ 3, at which quasars have been observed, would seem to be too early to allow pancakes to survive to the present. The survival of pancakes may be easier to arrange in a low density cosmological model since gravitational instability effectively ceases at redshifts z_f ~ 1 / ₀ - 1 but this would seem to be difficult to reconcile with the limits deduced from Eqs. (5.24).