


8.3. The pancake theory of galaxy formation
In Sections 4 and 5 we
described how photon viscosity and the decay
of neutrino perturbations can imprint characteristic mass scales on an
initial power-law spectrum of adiabatic perturbations. If neutrinos
are massless, the photon viscosity damping mass scale is given by Eq.
(4.12). For sufficiently low
 ( ~ 0.1) this
corresponds roughly to a
cluster of galaxies. Since perturbations on smaller mass-scales are
erased, the first; objects to collapse will be larger than individual
galaxies and will have masses far in excess of the Jeans mass after
recombination. Pressure forces are, therefore, negligible and so the
collapse may be described using the
Zel'dovich (1970)
approximate theory discussed in Section 5.2.
This predicts the formation of
pancakes. However, in contrast to the collisionless collapse
discussed in Section 5.2, the gas will form a
shock and the shocked
gas will be heated to a high temperature. In this Section, we
calculate the fraction of the shocked gas that can radiatively cool to
temperatures
( ~ 0.1) this
corresponds roughly to a
cluster of galaxies. Since perturbations on smaller mass-scales are
erased, the first; objects to collapse will be larger than individual
galaxies and will have masses far in excess of the Jeans mass after
recombination. Pressure forces are, therefore, negligible and so the
collapse may be described using the
Zel'dovich (1970)
approximate theory discussed in Section 5.2.
This predicts the formation of
pancakes. However, in contrast to the collisionless collapse
discussed in Section 5.2, the gas will form a
shock and the shocked
gas will be heated to a high temperature. In this Section, we
calculate the fraction of the shocked gas that can radiatively cool to
temperatures
 104 K
and thus the fraction of gas that can fragment
into galaxies. We also consider the characteristic masses of the first
fragments to condense from the cooled gas. Analytic and semi-analytic
discussions have been given by
Sunyaev and Zel'dovich
(1972),
Zel'dovich (1978),
Doroshkevich, Shandarin
and Saar (1978) and
Jones, Palmer and Wyse
(1981).
104 K
and thus the fraction of gas that can fragment
into galaxies. We also consider the characteristic masses of the first
fragments to condense from the cooled gas. Analytic and semi-analytic
discussions have been given by
Sunyaev and Zel'dovich
(1972),
Zel'dovich (1978),
Doroshkevich, Shandarin
and Saar (1978) and
Jones, Palmer and Wyse
(1981).
If neutrinos have a non-zero rest mass, the relevant damping mass is
given by Eq. (5.21). The same qualitative picture as outlined above
applies in this case, except that only a small fraction of the total
pancake mass is in baryonic form
( b /
b /
 T) which
can shock and cool.
The rest, (
T) which
can shock and cool.
The rest, (
 /
/
 T,
T,
 T =
T =

 +
+
 b) is
in massive neutrinos which are
collisionless. In this case, neutrinos and baryons collapse together
until the pancake forms. The baryons then shock while the neutrinos
can propagate through the caustic, leading to a neutrino-baryon sandwich
(Doroshkevich et
al., 1980).
In this scenario, one has a
natural explanation of the missing-mass in clusters of galaxies - a
problem that was never satisfactorily addressed in purely baryonic
versions of the pancake theory. Detailed numerical calculations of the
shock structure and the fraction of the gas which can cool in
neutrino-baryon pancakes are described by
Bond, Szalay and White
(1983) and
by Shapiro,
Struck-Marcell and Melott (1983).
b) is
in massive neutrinos which are
collisionless. In this case, neutrinos and baryons collapse together
until the pancake forms. The baryons then shock while the neutrinos
can propagate through the caustic, leading to a neutrino-baryon sandwich
(Doroshkevich et
al., 1980).
In this scenario, one has a
natural explanation of the missing-mass in clusters of galaxies - a
problem that was never satisfactorily addressed in purely baryonic
versions of the pancake theory. Detailed numerical calculations of the
shock structure and the fraction of the gas which can cool in
neutrino-baryon pancakes are described by
Bond, Szalay and White
(1983) and
by Shapiro,
Struck-Marcell and Melott (1983).
In the absence of any substantial primordial small-scale
fluctuations, such as might be expected, for example, in the hybrid
isothermal- adiabatic scenario envisaged by
Dekel (1983),
fragmentation is inhibited until a sufficiently dense
quasi-equilibrium gas layer has accumulated in the mid-plane of the
pancake. The pancake structure is determined as follows. The
trajectory of a fluid element initially at comoving coordinate
 measured perpendicular to the pancake plane is given, for a
one-dimensional pressure-free collapse, by
measured perpendicular to the pancake plane is given, for a
one-dimensional pressure-free collapse, by
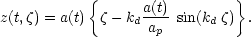 |
(8.16) |
This non-linear solution combines the Hubble flow (in the first term) with the influence of a linearized plane wave density perturbation on the Hubble flow (in the second term) and can be shown to be consistent both with the equations of motion and Poisson's equation (Zel'dovich, 1970). Mass conservation then yields
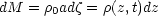 |
where
 0 is
the background density. A more general formulation in
terms of an arbitrary spectrum yields
0 is
the background density. A more general formulation in
terms of an arbitrary spectrum yields
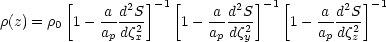 |
(8.17) |
where  is the Lagrangian
coordinate and S(
is the Lagrangian
coordinate and S( )
replaces
sin(kd
)
replaces
sin(kd )
in Eq. (8.16). Evidently, at a local maximum of
d2S /
d
)
in Eq. (8.16). Evidently, at a local maximum of
d2S /
d 2 infinite
density is attained in the midplane
(
2 infinite
density is attained in the midplane
( = 0) at a
redshift given by
a(t) = ap. This signifies the
formation of a caustic surface which arises
from the intersection of particle trajectories.
= 0) at a
redshift given by
a(t) = ap. This signifies the
formation of a caustic surface which arises
from the intersection of particle trajectories.
We can regard  as
prescribing the mass-fraction and z as the
instantaneous location of the particles initially in a plane-wave
perturbation of wave number k. The time evolution of the
particle density is given by
as
prescribing the mass-fraction and z as the
instantaneous location of the particles initially in a plane-wave
perturbation of wave number k. The time evolution of the
particle density is given by
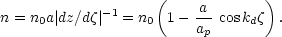 |
(8.18) |
This represents matter falling into the mid-plane as
a  ap, and n0 is
the initial density of the background. The velocity acquired in
free-fall is sufficiently great
(
ap, and n0 is
the initial density of the background. The velocity acquired in
free-fall is sufficiently great
( 103 km
s-1) that the infalling
matter shocks to a temperature > 108 K, and the density is
large enough near the midplane that the post-shock primordial gas
radiatively cools to ~ 104 K (although thermal conductivity may
maintain much of the gas at ~ 106 K). To evaluate the cooled
mass-fraction, we note that the cooling time-scale is
103 km
s-1) that the infalling
matter shocks to a temperature > 108 K, and the density is
large enough near the midplane that the post-shock primordial gas
radiatively cools to ~ 104 K (although thermal conductivity may
maintain much of the gas at ~ 106 K). To evaluate the cooled
mass-fraction, we note that the cooling time-scale is
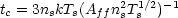 |
(8.19) |
where Aff< is the free-free cooling coefficient
and subscript s
denotes post-shock values, while the dynamical time scale of the newly
shocked gas is td = 4z /
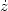 . Also the immediate
post-shock temperature is
. Also the immediate
post-shock temperature is
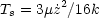 |
(8.20) |
where µ is the mean mass per H atom. Equating
tc and td and
letting a ~ ap yields the critical mass-fraction
 c that cools:
c that cools:
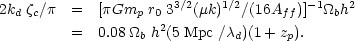 |
(8.21) |
For a neutrino sandwich with

 ~ 1, only a mass fraction
~ 1, only a mass fraction
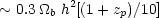 |
(8.22) |
enters the cooled baryonic layer at caustic formation. If
 b
b
 0.1
this means that no more than three percent of the closure density (and
about 30% of the total baryonic density) may be expected to
participate in galaxy formation when the cooled, compressed baryonic
pancake eventually fragments. Numerical simulations of one-dimensional
shocks confirm these simple estimates
(Bond et al., 1983).
0.1
this means that no more than three percent of the closure density (and
about 30% of the total baryonic density) may be expected to
participate in galaxy formation when the cooled, compressed baryonic
pancake eventually fragments. Numerical simulations of one-dimensional
shocks confirm these simple estimates
(Bond et al., 1983).
Since only the cooled gas fragments and forms galaxies, this leads
to a clear prediction of the pancake model: there should be at least a
factor three more hot gas in galaxy clusters than baryonic mass in
galaxies. Observationally, one finds M/L for rich
clusters to be of order
400h(M/L) , with ~ 10 - 20% of this accounted for by
hot X-ray emitting gas. Since the luminous regions of galaxies have
M/L ~ 10,
the pancake theory prediction will be satisfied provided that both
galaxy halos and the dark matter in galaxy clusters are
non-baryonic. One would not easily be able to reconcile this theory
with observation if halos and clusters were predominantly composed of
dissipative material, such as compact stellar remnants, which had not
undergone collapse prior to pancake formation.
, with ~ 10 - 20% of this accounted for by
hot X-ray emitting gas. Since the luminous regions of galaxies have
M/L ~ 10,
the pancake theory prediction will be satisfied provided that both
galaxy halos and the dark matter in galaxy clusters are
non-baryonic. One would not easily be able to reconcile this theory
with observation if halos and clusters were predominantly composed of
dissipative material, such as compact stellar remnants, which had not
undergone collapse prior to pancake formation.
The minimum fragment mass turns out to be relatively small. The cool gas layer is ram-pressure confined, and the minimum mass that is gravitationally unstable is given by the criterion (Sunyaev and Zel'dovich, 1972):
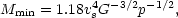 |
(8.23) |
where vs is the sound velocity and p is the ram pressure. Now
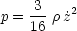 |
and is independent of
 (for
kd
(for
kd  << 1). Consequently, one obtains
<< 1). Consequently, one obtains
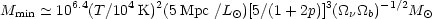 |
(8.24) |
It seems unlikely that one could avoid fragmentation down to
Mmin. This is much smaller than the mass of a
typical galaxy, so
galaxy formation must presumably occur by the aggregation of many
smaller clouds of mass 107 - 109
M ,
much as in the primordial isothermal fluctuation model
(Doroshkevich, Shandarin
and Saar, 1978).
The principal difference now is that the clouds originate by fragmentation
at the relatively late epoch of pancaking, and so perhaps are more
likely to be predominantly gaseous as galaxies form.
,
much as in the primordial isothermal fluctuation model
(Doroshkevich, Shandarin
and Saar, 1978).
The principal difference now is that the clouds originate by fragmentation
at the relatively late epoch of pancaking, and so perhaps are more
likely to be predominantly gaseous as galaxies form.