2.9. Dynamics of galaxies in clusters

In Sections 2.5, 2.6, and 2.7, evidence was presented indicating that the velocity and spatial distribution of galaxies in regular, compact clusters are in a relaxed, quasistationary state. In this section, the nature of the relaxation processes of galaxies in clusters will be briefly discussed.

If clusters result from the gravitational growth of initially small perturbations, we expect the initial state of material in the protocluster to be irregular. The relaxation of the cluster thus involves the spatial motion of the galaxies, and a lower limit to the relaxation time is the crossing time

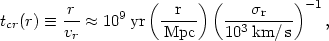
(2.26)

where the radial velocity dispersion _r has been substituted for the radial velocity v_r. An upper limit on the age of the cluster is the Hubble time (age of the universe)

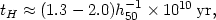
(2.27)

where the numerical coefficient depends on the cosmological model. Thus the outer parts of a cluster or surrounding supercluster for which r 10 Mpc cannot possibly have relaxed and are expected to be irregular, as is observed (Sections 2.7 and 2.11.2).

2.9.1. Two-body relaxation

The phase-space distribution of galaxies in the central parts of spherical regular clusters can be represented as f(r, v) exp(- / _r²), where 1/2 v² + (r) is the energy per unit mass in the cluster (Section 2.7). This is very similar to a Maxwell-Boltzmann distribution, except that it is the energy per unit mass (velocity dispersion) which is determined, and not the energy (temperature). We first consider the possibility that clusters have relaxed thermodynamically.

Thermodynamic equilibrium could result from elastic collisions between galaxies, and would be expected if the time scale for energy transfer in such collisions were shorter than the age of the cluster or the time-scale for the loss of kinetic energy through dissipative processes. The most important elastic two-body collisions in a cluster are gravitational. The resulting relaxation times have been calculated analytically by Chandrasekhar (1942) and Spitzer and Harm (1958), and numerically through N-body simulations, including a realistic luminosity function for galaxies by White (1976c, 1977b) and Farouki and Salpeter (1982). A useful characteristic time-scale (0.94 times the Spitzer 'reference time') is

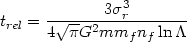
(2.28)

for the relaxation of a galaxy of mass m in a background field of galaxies of mass m_f and number density n_f. is the ratio of maximum to minimum impact parameters of collisions which contribute to the relaxation; the maximum impact parameter is on the order of half the gravitation radius of the cluster R_G (equation 2.21), while the minimum impact parameter is roughly the larger of the galaxy radius r_g or the 'turning radius' Gm_f / 3_r² (White, 1976b). Thus

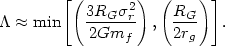
(2.29)

Usually, the second value applies. Thus, for r_g 20 kpc, R_G 1 Mpc, ln 3.

In order to give a lower limit to the relaxation time, we assume for the moment that all the mass in a cluster (including the missing mass (Section 2.8)) is bound to individual galaxies; we later show this is unlikely to be the case. Then, we define an average density <> 3M_tot / (4 R_G³), where M_tot is the total mass of the cluster. If we assume a Schechter luminosity function (equation 2.3), and a fixed galaxy mass-to-light ratio, we find

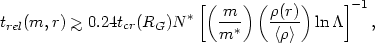
(2.30)

where m^* is the characteristic galaxy mass (corresponding to L^*), N^* is the characteristic galaxy number (richness), t_cr is the cluster crossing time (equation 2.26), and (r) is the total cluster density at r. Equation (2.30) is a lower limit because it assumes all the cluster mass is bound to individual galaxies. Typically, R_G 1 Mpc, _r 1000 km/s, N^* 1000, and ln 3, giving t_cr(R_G) 10⁹ yr and t_rel(m^*, R_G) 3 × 10¹¹ yr. This is much longer than a Hubble time (equation 2.27); it is therefore unlikely that the apparently relaxed state of regular clusters results from two-body collisions. However, two-body relaxation processes can affect the more massive galaxies (m >> m^*) near the cluster center ((r) >> <>), as is discussed below.