2.8. Cluster masses-the missing mass problem

The masses of clusters of galaxies can be determined if it is assumed that they are bound, self-gravitating systems. Cluster masses were first derived by Zwicky (1933) and Smith (1936). They found that the masses greatly exceed those which would be expected by summing the masses of all the cluster galaxies. Reviews of cluster mass determinations include Faber and Gallagher (1979) and Rood (1981).

If clusters were not bound systems, they would disperse rather quickly (in a crossing time t_cr 10⁹ years). Because many clusters appear regular and relaxed, and because their galactic content is quite different from that of the field, it is very unlikely that the regular compact clusters are flying apart. Assuming they are held together by gravity, one limit on the mass of clusters comes from the binding condition,

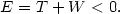
(2.17)

Here E is the total energy, t the kinetic energy, and W the gravitational potential energy:

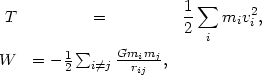
(2.18)

where the sums are over all galaxies, m_i and v_i are the galaxy mass and velocity, and r_ij is the separation of galaxies i and j.

A stronger mass limit results if we assume that the cluster distribution is stationary. The equations of motion of galaxies can be integrated to give

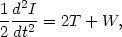
(2.19)

where I = m_i r_i² is the moment of inertia measured from the center of mass. For a stationary configuration, the left-hand-side of equation (2.19) is zero, and

(2.20)

This is the virial theorem. The total cluster mass is M_tot = m_i; we can define a mass weighted velocity dispersion <v²> m_i v_i² / M_tot, and gravitational radius

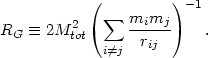
(2.21)

Then, the virial theorem gives

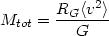
(2.22)

Now, <v²> and R_G can be evaluated from the radial velocity distribution and the projected spatial distribution of a fair sample of galaxies if one assumes that the positions of galaxies and the orientation of their velocity vectors are uncorrelated. Then, <v²> = 3_r², where _r is the (mass-weighted) radial velocity dispersion, and R_G = /2 b_G (Limber and Mathews, 1960), where

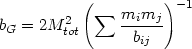
(2.23)

and b_ij is the projected separation of galaxies i and j. Alternatively, R_G can be calculated from a fit to the galaxy distribution (as in Section 2.7) or from strip counts of galaxies (Schwarzschild, 1954). Combining these we have

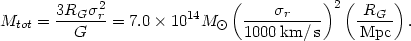
(2.24)

Since _r 10³ km/s and R_G 1 Mpc for an average rich cluster, one finds M_tot 10¹⁵ M typically.

The virial theorem requires that one sum over all the particles in a cluster; it can only be directly applied to galaxies alone if the contain all of the mass in the cluster. One can also derive the mass of a cluster by treating the galaxies as test particles in dynamical equilibrium in the gravitational potential of the cluster. Such calculations generally give results for the total mass which are consistent with the virial theorem determinations; usually, one must assume that the galaxies and the total mass have the same spatial distribution. The most accurate of these determinations involve comparing numerical or analytical models for the galaxy distribution in a cluster with the observed spatial and velocity distributions (White, 1976c; Kent and Gunn, 1982; Kent and Sargent, 1983). The best data exist for the Coma and Perseus clusters; the masses for both these clusters are about 3 × 10¹⁵ M within a projected radius of 3° from the cluster center (Kent and Gunn, 1982; Kent and Sargent, 1983).

These analyses give surprisingly large masses for clusters, particularly when compared to the total luminosity of a cluster L_tot 10¹³ L. The conventional method of quantifying this comparison is to calculate the mass-to-light ratio of a system in solar units (M_tot / L_tot) / (M / L). Obviously, any system composed solely of stars like our Sun would have a mass-to-light ratio of unity. Mass-to-light ratios have been derived for a number of clusters using the virial theorem and the measured magnitudes of the galaxies at visual (V) or blue (B) magnitudes Typically (see Faber and Gallagher, 1979, and Rood, 1981, and references in these reviews) one finds

(2.25)

The mass-to-light ratios found for the luminous portions of galaxies range from (M/L_B)_gal (1 - 12)h₅₀ M / L, with the large values corresponding to the E and S0 galaxies which predominate in compact regular clusters. Thus only about 10% of the mass in clusters can be accounted for by material within the luminous portions of galaxies. This is the so-called 'missing mass' problem, although this is something of a misnomer. It is not the mass which is missing; what is missing is any other evidence for this invisible matter. The application of the virial theorem to clusters and the discovery that most of their mass was nonluminous was first made by Zwicky (1933) and Smith (1936).

How secure are these mass determinations for clusters? As long as a fair sample of galaxies are observed, the virial theorem masses are insensitive to velocity anisotropies, although this can be a problem if only galaxies near the cluster center are used. The dynamical model estimates for the masses are also not affected much by velocity anisotropies (Kent and Gunn, 1982). The virial theorem applies even if most galaxies are bound in binaries or subclusters, as long as the velocities and positions are measured for a fair sample of galaxies and R_G is computed directly from the galaxy positions. However, galaxies are not generally bound in binaries in regular clusters (Abell, Neyman, and Scott, 1964), and in any case typical binary or group velocities are too small to contribute significantly to _r (however, see Noonan, 1975). If the clusters are bound but not relaxed, equation 2.17 would give a mass lower by only a factor of two than equation 2.20. The velocity dispersion and R_G of a cluster might be contaminated by field galaxies. This background contamination problem can be reduced by determining the mass-to-light ratio for the core of a regular cluster, using the core parameters of an isothermal model fit (Section 2.7). Again, one typically finds (M/L_V)_core 300h₅₀ M / L (Rood et al., 1972; Bahcall, 1977a; Dressler, 1978b).

In principle, the missing mass could be associated with a large number of low luminosity, large M/L galaxies (see Noonan, 1976; Section 2.4). Such galaxies could affect the mass-to-light ratio if they made a significant contribution to the total light of a cluster which was not included in the usual determinations of the total luminosity because the galaxies were too faint to be detected individually. However, these galaxies would then produce a significant amount of diffuse light between galaxies in a cluster. Observations of the diffuse light in the Coma cluster show that its luminosity is at most comparable to that in bright galaxies (de Vaucouleurs and de Vaucouleurs, 1970; Melnick et al., 1977; Thuan and Kormendy, 1977). Thus the required mass-to-light ratios cannot be greatly affected by low mass galaxies. Abell (1977) included a large number of low mass galaxies in his determination of the mass-to-light ratio in Coma, and found a value about a factor of two smaller than that in equation (2.25).

There is now considerable direct and indirect evidence for invisible matter associated directly with individual galaxies as well as clusters (see Faber and Gallagher, 1979, and Rood, 1981, for extensive reviews). It has been suggested that the invisible matter forms an extended halo around non-cluster galaxies, extending significantly further than the luminous material and having at least several times more mass (Einasto et al., 1974; Ostriker et al., 1974).

The nature of this missing mass component in clusters and galaxies remains one of the most important unsolved problems in astrophysics. Careful searches have been made for diffuse radiation in clusters, which might be produced if the missing mass were gaseous or stellar. These have included searches for radio free-free emission (Davidsen and Welch, 1974), optical and UV line emission (Crane and Tyson, 1975; Bohlin et al., 1973), optical continuum emission (de Vaucouleurs and de Vaucouleurs, 1970; Melnick et al., 1977; Thuan and Kormendy, 1977), and 21 cm radio emission from neutral hydrogen (Shostak et al., 1980). The observations of X-ray emission from clusters, which are the primary subject of this book, also give limits on the mass of hot gas (Section 5.4.1). These studies and other similar searches have shown that the missing mass is not diffuse gas at any temperature, not dust grains of the type found in the interstellar medium, and not luminous stars.

In general, most suggestions as to the identity of the missing mass fall into three categories:

1. substellar mass condensations, such as stars with mass < 0.1M (Ostriker, Peebles, and Yahil, 1974), planetary size bodies, or comets (Tinsley and Cameron, 1974);
2. invisible remnants of massive stars (black holes, neutron stars, or cool white dwarfs);
3. stable, weakly interacting elementary particles, such as massive neutrinos, magnetic monopoles, axions, photinos, etc. (Blumenthal et al., 1984).

Where is this missing mass located? A number of arguments suggest that the total mass distribution is similar to the galaxy distribution (Rood et al., 1972). The fact that the galaxy distributions in compact, regular clusters are reasonably represented by isothermal spheres and that core and total mass-to-light ratios are equal within the errors supports this view. On the other hand, Smith et al. (1979b) and Smith (1980) have argued that the galaxy and mass distributions can be very dissimilar if the galaxies collapsed after the cluster potential was established. However, in this case violent relaxation (Section 2.9.2) is not effective, clusters could not have compact cores, and the mass-to-light ratio in the inner regions would not be the same as that for the entire cluster.

Is the missing mass bound to individual galaxies in clusters? Probably not. The rate of two-body relaxation (dynamical friction) of galaxies in clusters is proportional to galaxy masses (Section 2.9.1). If the missing mass were distributed among galaxies in proportion to their luminosity, very significant mass segregation would be expected (Rood, 1965; White, 1977b), which is not seen (Section 2.7). Moreover, if the missing mass were bound to galaxies in haloes having velocity dispersions similar to those in their visible portions, then the haloes would have to extend roughly 0.5 Mpc from the galaxy center (White, 1985). This is much larger than the typical separations of galaxies in the cores of clusters. Thus the missing mass probably forms a continuum, occupying the entire volume of the cluster, but with an overall density distribution fairly similar to that of the galaxies.

Although the missing mass is probably not currently bound to individual galaxies, it may initially have formed massive haloes around individual galaxies, which were stripped by tidal interactions during and after the formation of the cluster (Richstone, 1976, and Section 2.10.1). As mentioned above, there is considerable evidence that more isolated galaxies are immersed in extensive massive haloes (see reviews by Faber and Gallagher, 1979, and Rood, 1981). However, the time scales for tidal interactions and dynamical friction are similar; it is not clear, therefore, that tidal interactions will strip the massive haloes before galaxies merge. The problem of the competition between tidal forces and dynamical friction is the subject of a number of recent investigations (Richstone and Malumuth, 1983; Malumuth and Richstone, 1984; Merritt, 1983, 1984a, b, 1985; Miller, 1983), which unfortunately reach contradictory conclusions (Section 2.10.1). This problem is particularly serious for the massive binary galaxies which dominate B clusters (Section 2.5).

Alternatively, the missing mass in clusters may never have been associated with galaxies. For example, the missing mass may be more extensive than the luminous material; the luminous matter, may only be the 'tip of the iceberg' of the real mass distribution. Rood et al. (1970) found that M/L increased with the scale size of the system (see also Rood, 1981), which supports this hypothesis; however, Turner and Sargent (1974) have argued that this was an artifact of calculating M from equation (2.22).

In many ways, a much better way to determine the masses of clusters of galaxies and the distribution of the missing mass is to apply the hydrostatic equation to the distribution of hot intracluster gas. This method, which is discussed in Section 5.5.5, avoids any assumption about the shapes of the orbits of galaxies, since the velocities of the particles in the gas are isotropic.