2.9.2. Violent relaxation

The fact that clusters exhibit a nearly constant velocity dispersion (rather than kinetic temperature) suggests that the relaxation is produced by collective gravitational effects. Lynden-Bell (1967) showed that collective relaxation effects can result in a very rapid quasi-relaxation ('violent relaxation'). The existence of these effects involves a somewhat subtle point; collective relaxation develops through collisionless interactions, and thus the detailed ('fine-grain') phase-space distribution of galaxies is conserved. However, if the relaxation is sufficiently violent (for example, the energy of particles is changed by a significant fraction), then initially adjoining units of phase-space will be widely separated in the final state ('phase mixing'). Thus, if one averages the fine-grain phase-space density over any observable volume to give a 'coarse-grain' distribution, this coarse-grain distribution can be an equilibrium distribution and independent of the details of the initial state.

If clusters were formed by the growth and collapse of initial perturbations, then during the collapse the gravitational potential fluctuated violently. This would cause a change in the energy per unit mass 1/2 v² + (r) of

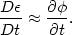
(2.31)

For example, if the cluster collapsed from a stationary state (v = 0) to a virialized final state (Section 2.8), then . The time scale for collapse t_coll is roughly a dynamical time scale or crossing time

(2.32)

As the energy of a galaxy changes by 100% during a collapse time, violent relaxation can be completed during the collapse of the cluster, after which time the potential is constant, and the galaxy distribution is in stationary virial equilibrium.

Since the equation of motion of a particle in the cluster's mean gravitational field is independent of mass (equation 2.31), the equilibrium is independent of mass. Lynden-Bell (1967) derived an equilibrium state by assuming that the system relaxed to the most probable coarse-grained phase-space state subject to conservation of energy, particle number, and fine-grain phase density. This equilibrium state was found to be a Fermi-Dirac distribution that reduces to the Maxwell-Boltzmann distribution for the appropriate number densities in clusters (see also Shu, 1978),

(2.33)

This phase space density produces a Gaussian velocity distribution and isothermal spatial distribution of galaxies, which are roughly consistent with the observed distributions in the inner parts of clusters (Sections 2.6 and 2.7). The distribution is also independent of mass, roughly as observed. If equation (2.33) held for all radii, the cluster mass would be infinite (Section 2.7). However, galaxies at large radii or with large energies never reach equilibrium because their crossing times (equation 2.26) are longer than the Hubble or collapse times (equations 2.27 and 2.32). Because the relaxation occurs only while the cluster is collapsing, it is not clear that this equilibrium state can ever be achieved in any real collapsing system.

The state of equilibrium of a collisionless, gravitationally collapsing system can be studied directly through numerical N-body experiments. These experiments do show that isolated collapsing or merging systems relax rapidly (in a few crossing times), and they agree roughly on the nature of the equilibrium state. In general, they do not find that the systems become isothermal spheres; instead they find spatial distributions that are reasonably represented by the de Vaucouleurs (1948a, b; equation 2.14) or Hubble (1930; equation 2.15) forms (White, 1979; Villumsen, 1982; van Albada, 1982). These distributions are more centrally condensed and fall off more rapidly at large radii than the isothermal sphere. However, it is possible that the subsequent collapse of surrounding material can increase the density at large distances; Gunn (1977) has shown that for some initial conditions this process can lead to nearly isothermal mass distributions.

The idea that the distribution of galaxies in clusters is determined by violent relaxation during the formation of the cluster provides a simple explanation for the one-dimensional morphological sequence of clusters running from irregular to regular (Table 1; Gunn and Gott, 1972; Jones et al., 1979; Dressler, 1984). The regular clusters are those old enough to have collapsed and relaxed, while the irregular ones have not. As the collapse time is t_coll (R_h³ / GM_tot)^1/2 (G_i)^-1/2, where _i is the initial density, higher density protoclusters will collapse more rapidly. Since the age of clusters is limited by the Hubble time t_h, regular clusters will be produced by higher density protoclusters, and irregular clusters by lower density protoclusters. Thus we expect regular clusters to have higher densities than irregular clusters, as is observed. Moreover, violent relaxation and phase mixing will eliminate subclustering and produce a centrally condensed, symmetric distribution, as observed in regular clusters.

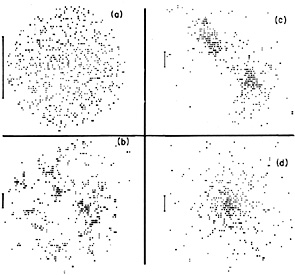
White (1976c) has followed the collapse of a model cluster numerically, with an N-body code; the results are shown in Figure 5. He finds that the cluster first forms irregular subcondensations around massive galaxies (like an I cluster). These continually merge until the galaxy distribution is elongated and has two large clumps (like an F cluster), which merge to form a smooth, regular cluster with a prominent core (a C cluster) (see also Henry et al., 1981; Forman and Jones, 1982). Recently, Cavaliere et al. (1983) have produced many similar models for cluster collapse.

Figure 5. The projected galaxy distributions in White's (1976c) N-body calculations of the evolution of a collapsing cluster. Each symbol represents a galaxy. In each figure, the bar represents a fixed length scale, one-half of the gravitational radius RG (equation 2.21). The times t are given in units of the initial collapse time of the cluster. (a) The initial configuration (t = 0). (b) An irregular distribution with subclustering at t = 0.19. (c) A bimodal distribution in the cluster at t = 0.97. (d) The final relaxed configuration at t = 2.66.

The other aspects of the morphological sequence have to do with galactic content-the fractions of spiral, S0, and elliptical galaxies, or domination by supergiant (B, D, and cD) galaxies. In Section 2.10 evidence is presented which suggests that the galactic content of clusters is also determined by the density of the cluster, although the mechanism is still controversial.