Copyright © 1994 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1994. 32:
319-70 Copyright © 1994 by Annual Reviews. All rights reserved |
1.2. Sources of
 T /
T
T /
T
In the standard recombination picture, the cosmic plasma becomes neutral, and the microwave background photons are last scattered at redshifts z ~ 1100. Hence any observed variation in the intensity of these photons gives us direct information about the Universe at that epoch, and potentially much earlier when the fluctuations were initially laid down. The theory behind microwave background anisotropies is reviewed by Kaiser & Silk (1986), Bond (1988), Efstathiou (1990), and others. Several effects contribute to fluctuations in the observed temperature of the radiation. Schematically, in rough order of importance with decreasing angular scale:
 |
 T / T =
V T / T =
V /
c /
c |
dipole anisotropy, where
V is our
motion relative to the radiation; is our
motion relative to the radiation; |
 |
 T / T
= - T / T
= - 
 |
gravitational potential or Sachs-Wolfe fluctuations; |
 |
 T / T
= 1/3 T / T
= 1/3
 / /
 |
if the perturbations are adiabatic; |
 |
 T / T
= - 1/3 T / T
= - 1/3 S S |
if the perturbations are isocurvature; |
 |
 T / T =
v/c T / T =
v/c |
Doppler shifts, when the photons were last scattered; |
 |
 T / T
= - 2kTe/(mec2) T / T
= - 2kTe/(mec2) |
Sunyaev-Zel'dovich fluctuations caused by scattering off hot electrons. |
We are not concerned here with the dipole contribution (which up
until COBE was the only measured temperature variation), since it is
"extrinsic:" being caused by our local motion
(Peebles & Wilkinson
1968).
[The "intrinsic" dipole is expected to be of similar amplitude
to the quadrupole, i.e. ~ 100 times smaller; similarly the "extrinsic"
quadrupole has amplitude 1/2(v / c) of the dipole.]
Sachs-Wolfe
(Sachs & Wolfe 1967)
fluctuations dominate at the largest scales, above that
subtended by the horizon at last scattering. The sum of the
gravitational redshift effect plus the intrinsic fluctuation leads to
 T / T =
- 1/3
T / T =
- 1/3
 for adiabatic
perturbations (see Appendix B;
Section 2.4).
for adiabatic
perturbations (see Appendix B;
Section 2.4).
Large-scale anisotropies are higher in the case of isocurvature perturbations because the potential and intrinsic fluctuations add rather than partially canceling (Efstathiou & Bond 1986, Kodama & Sasaki 1986; see Section 2.4). These large-scale fluctuations are largely independent of any reionization, simply because no causal process during the scattering epoch can affect scales larger than the horizon size. At scales smaller than this, the radiation perturbations relax to a state of pressure equilibrium; therefore there are essentially no fluctuations caused by the peculiar gravity at small scales (Kaiser 1984).
Whether Sunyaev-Zel'dovich
(Zel'dovich & Sunyaev
1969;
Sunyaev & Zel'dovich
1970,
1972)
fluctuations will be important depends on
details of the distribution of hot electrons during a possible
reionization. They will be largest in pancake
(Szalay et al 1983,
SubbaRao et al 1994),
explosion
(Hogan 1984),
or other models with significant reheating. However
 T / T ~
10-5 is expected in nearby rich clusters on arc-minute scales
(e.g. Sunyaev 1978,
Rephaeli 1981,
Bond 1988,
Schaeffer & Silk 1988,
Cole & Kaiser 1988,
Trester & Canizares
1989,
Cavaliere et al 1991,
Bond & Myers 1991,
Makino & Suto 1993),
irrespective of reionization, with fluctuations in arbitrary
directions an order of magnitude smaller (e.g.
Markevitch et al 1991,
Scaramella et al 1993).
This effect causes a spectral distortion,
which is easiest to observe as a decrement in the Rayleigh-Jeans part,
and hence can be distinguished from the other effects, which are
primeval in origin
(Sunyaev & Zel'dovich
1972,
Zel'dovich et al 1972).
S-Z distortions have been seen in a few of the richest clusters (e.g.
Gull & Northover 1976;
Birkinshaw et al 1981,
1984;
Uson 1986;
Birkinshaw 1990;
Klein et al 1991;
Herbig et al 1992;
Birkinshaw et al 1993;
Wilbanks et al 1993;
Jones et al 1993).
T / T ~
10-5 is expected in nearby rich clusters on arc-minute scales
(e.g. Sunyaev 1978,
Rephaeli 1981,
Bond 1988,
Schaeffer & Silk 1988,
Cole & Kaiser 1988,
Trester & Canizares
1989,
Cavaliere et al 1991,
Bond & Myers 1991,
Makino & Suto 1993),
irrespective of reionization, with fluctuations in arbitrary
directions an order of magnitude smaller (e.g.
Markevitch et al 1991,
Scaramella et al 1993).
This effect causes a spectral distortion,
which is easiest to observe as a decrement in the Rayleigh-Jeans part,
and hence can be distinguished from the other effects, which are
primeval in origin
(Sunyaev & Zel'dovich
1972,
Zel'dovich et al 1972).
S-Z distortions have been seen in a few of the richest clusters (e.g.
Gull & Northover 1976;
Birkinshaw et al 1981,
1984;
Uson 1986;
Birkinshaw 1990;
Klein et al 1991;
Herbig et al 1992;
Birkinshaw et al 1993;
Wilbanks et al 1993;
Jones et al 1993).
At small angular scales, the dominant mechanisms are the adiabatic fluctuations (Silk 1967) and scattering off moving electrons (Sunyaev & Zel'dovich 1970). In addition there is a complication at small scales, caused by gravitational tensing of the microwave background radiation by clustered matter (Chitre et al 1986; Blanchard & Schneider 1987; Kashlinsky 1988; Linder 1988a, 1990; Feng & Liu 1992), but Cole & Efstathiou (1989), Tomita & Watanabe (1989), and Sasaki (1989) have shown that the effects are negligible for most models of galaxy formation, except perhaps at sub-arcminute scales (Cayon et al 1993a, b, 1994). Lensing can enhance fluctuations on the smallest scales; the effect can be considered as observing the CMB with a beamwidth of order the dispersion of deflection angles. Furthermore, discrete sources at high redshift, with their radiation reprocessed by one of several emission mechanisms, could produce frequency-dependent fluctuations which would increase toward small angular scales (e.g. Dautcourt 1977; Sunyaev 1977, 1978; Hogan 1980, 1982; Korolev et al 1986; Bond et al 1986, 1991a). Of course, faint radio sources, as well as diffuse emission from our own Galaxy, can give anisotropies, although these are normally regarded as a contaminant rather than a source (e.g. Danese et al 1983; Banday & Wolfendale 1990, 1991a, b; Banday et al 1991; Franceschini et al 1989; Masi et al 1991; Brandt et al 1994).
Schematically, calculations of the contribution from different sources are performed via an integral through the scattering surface (see, however, Section 5.1). For example, for the Doppler-induced variations, the total perturbation to the radiation temperature can be expressed as:
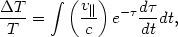
| (2) |
where the integrand is evaluated at time t, with
 the optical depth
measured from the present back to t, and v||
the component of peculiar
velocity along the line of sight. The exponential factor is an
approximation which allows for the effect of multiple scatterings - a
very good approximation since the predicted fluctuations are so small.
the optical depth
measured from the present back to t, and v||
the component of peculiar
velocity along the line of sight. The exponential factor is an
approximation which allows for the effect of multiple scatterings - a
very good approximation since the predicted fluctuations are so small.
In fact, to obtain accurate estimates of the fluctuations, and to determine the angular power spectrum, numerical calculations need to be done (see Section 3.2). However, there are semi-analytical methods for either standard recombination, using the tight-coupling limit [which gives both the matter and radiation spectra (Doroshkevich et al 1978; Bonometto et al 1983, 1984; Starobinskii 1988; Doroshkevich 1988; Atrio-Barandela et al 1991; Nasel'skii & Novikov 1993; Jørgensen et al 1993, 1994; Dodelson & Jubas 1994, Atrio-Barandela & Doroshkevich 1994a)] or for reionization, using the free-streaming approximation [which assumes a given Tm(k) (Vishniac 1987, Efstathiou 1988, Hu et al 1994, Atrio-Barandela & Doroshkevich 1994b)].