B.4.4. The Angular Structure of Lenses

Assuming you have identified all the halos needed to model a particular lens, there are three sources of angular structure in the potential. The first source is the shape of the luminous lens galaxy, the second source is the dark matter in the halo of the lens, and the third source is perturbations from nearby objects or objects along the line of sight. Of these, the only one which is easily normalized is the contribution from the stars in the lens galaxy, since it must be tightly connected to the monopole deflection of the stars. The observed axis ratios of early-type galaxies show a deficit of round galaxies, a plateau for axis ratios from q ~ 0.9 to q ~ 0.5 and then a sharp decline beyond q ~ 0.5 (e.g. Khairul & Ryden [2002]). Not surprisingly, the true elliptical galaxies are rounder than the lenticular (S0) galaxies even if both are grouped together as early-type galaxies. In three dimensions, the stellar distributions are probably close to oblate with very modest triaxialities (e.g. Franx et al. [1991]). Theoretical models of galaxy formation predict ellipticities and triaxialities larger than observed for luminous galaxies and show that the shapes of the dark matter halos are significantly modified by the cooling baryons (Dubinski [1992], [1994], Warren et al. [1992], Kazantzidis et al. [2004]). Local estimates of the shape of dark matter halos are very limited (e.g. Olling & Merrifield [2001], Buote et al. [2002]). Stellar isophotes also show deviations from perfect ellipses (e.g. Bender et al. [1989], Rest et al. [2001]) and the deviations of simulated halos from ellipses have a similar amplitude (Heyl et al. [1994], Burkert & Naab [2003]).

It is worth considering two examples to understand the relative importance of the higher order multipoles of a lens. The first is the singular isothermal ellipsoid (SIE) introduced in Section B.3 (Eqns. B.38-B.40). Let the major axis of the model lie on the ₁ axis, in which case only the cos(m) multipoles with m = 2, 4, ^... are non-zero. All non-zero poles also have the same radial dependence, with _cm = A_m / and _cm = - 2A_m / (m² - 1). The ratio of the internal to the external multipole depends only on the index of the multipole, _cm,int / _cm,ext = (m - 1) / (m + 1). Note, in particular, that the quadrupole moment of an SIE is dominated by the matter outside any given radius, with an internal quadrupole fraction of

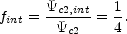(B.74)

For lenses dominated by dark matter halos that have roughly flat global rotation curves, most of the quadrupole moment is generated outside the Einstein ring of the lens (i.e. by the halo!). This will hold provided any halo truncation radius is large compared to the Einstein ring radius. The tangential deflection is larger than the radial deflection, with |_cm,rad / _cm,tan| = 1 / m. The final question is the relative amplitudes between the poles. The ratio of the angular deflection from the m = 2 quadrupole to the radial deflection of the monopole is

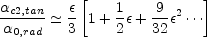(B.75)

while the ratio for the m = 4 quadrupole is

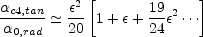(B.76)

where the axis ratio of the ellipsoid is q = 1 - . Each higher order multipole has an amplitude _m ^m/2 to leading order.

The relative importance of the higher order poles can be assessed by computing the deflections for a typical lens with the monopole deflection (essentially the Einstein radius) fixed to be one arc second. Using the leading order scaling of the power-series, but setting the numerical value to be exact for an axis ratio q = 1/2, the angular deflection from the quadrupole is 0."46 and that from the m = 4 pole is 0."09 ², while the radial deflections will be smaller by a factors of 2 and 4 respectively. Since typical astrometric errors are of order 0."005, the quadrupole is quantitatively important for essentially any ellipticity while the m = 4 pole becomes quantitatively important only for q 0.75 (and the m = 6 pole becomes quantitatively important for q 0.50).

In Fig. B.22 we compare the SIE to ellipsoidal de Vaucouleurs and NFW models. Unlike the SIE, these models are not scale free, so the multipoles depend on the distance from the lens center in units of the major axis scale length of the lens, R_major. The behavior of the de Vaucouleurs model will be typical of any ellipsoidal mass distribution that is more centrally concentrated than an SIE. Although the de Vaucouleurs model produces angular deflections similar to those of an SIE on small scales (for the same axis ratio), these are beginning to decay rapidly at the radii where we see lensed images (1 - 2R_major) because most of the mass is interior to the image positions and the amplitudes of the higher order multipoles decay faster with radius than the monopole (see Eqn. B.48). Similarly, as more of the mass lies at smaller radii, the quadrupole becomes dominated by the internal quadrupole. The NFW model has a somewhat different behavior because on small scales it is less centrally concentrated than an SIE (a 1 / r central density cusp rather than 1 / r²). It produces a somewhat bigger quadrupole for a given axis ratio, and an even larger fraction of that quadrupole is generated on large scales. In a "standard" dark matter halo model, the region with < R_major is also where we see the lensed images. On larger scales, the NFW profile is more centrally concentrated than the SIE, so the quadrupole begins to decay and becomes dominated by the internal component.

Figure B.22. Behavior of the angular multipoles for the de Vaucouleurs (solid), SIE (dashed) and NFW (dotted) models with axis ratios of either q = 0.75 (Top) or q = 0.5 (Bottom) as a function of radius from the lens center in units of the lens major axis scale Rmajor. For each axis ratio, the lower panel shows the ratio of the maximum angular deflections produced by the quadrupole (m = 2) and the m = 4 pole relative to the deflection produced by the monopole (m = 0). The upper panel shows the fraction of the quadrupole generated by the mass interior to each radius.

It is unlikely that mass distributions are true ellipsoids producing only even poles (m = 2, 4, ^... ) with no twisting of the axes with radius. For model fits we need to consider the likely amplitude of these deviations and the ability of standard terms to absorb and mask their presence. It is clear from Fig B.22 that the amplitude of any additional terms must be of order the m = 4 deflections expected for an ellipsoid for them to be important. Here we illustrate the issues with the first few possible terms.

A dipole moment (m = 1) corresponds to making the galaxy lopsided with more mass on one side of the lens center than the other. Lopsidedness is not rare in disk galaxies (~ 30% at large radii, Zaritsky & Rix [1997]), but is little discussed (and hence presumably small) for early-type galaxies. Certainly in the CASTLES photometry of lens galaxies we never see significant dipole residuals. It is difficult (impossible) to have an equilibrium system supported by random stellar motions with a dipole moment because the resulting forces will tend to eliminate the dipole. Similar considerations make it difficult to have a dark matter halo offset from the luminous galaxy. Only disks, which are supported by ordered rather than random motion, permit relatively long-lived lopsided structures. Where a small dipole exists, it will have little effect on the lens models unless the position of the lens galaxy is imposed as a stringent constraint. The reason is that a dipole adds terms to the effective potential of the form ₁ G() whose leading terms are degenerate with a change in the unknown source position.

Perturbations to the quadrupole (relative to an ellipsoid) arise from variations in the ellipticity or axis ratio with radius. Since realistic lens models require an independent external shear simply to model the local environment, it will generally be very difficult to detect these types of perturbations or for these types of perturbations to significantly modify any conclusions. In essence, the amplitude and orientation of the external shear can capture most of their effects. Their actual amplitude is easily derived from perturbation theory. For example, if there is an isophote twist of between the region inside the Einstein ring and outside the Einstein ring, the fractional perturbations to the quadrupole will be of order , or approximately / 3 of the monopole - independent of the ability of the external shear to mimic the twist, the actual amplitude of the perturbation is approaching the typical measurement precision unless the twist is very large. Only in Q0957+561 have models found reasonably clear evidence for an effect arising from isophotal twists and ellipticity gradients, but both distortions are unusually large in this system (Keeton et al. [2000]). In general, in the CASTLES photometry of lens galaxies, deviations from simple ellipsoidal models are rare.

Locally we observe that the isophotes of elliptical galaxies are not perfect ellipses (e.g. Bender et al. [1989], Rest et al. [2001]) and simulated halos show deviations of similar amplitude (Heyl et al. [1994], Burkert & Naab [2003]). For lensing calculations it is useful to characterize these perturbations by a contribution to the lens potential and surface density of

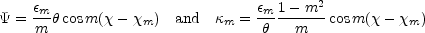(B.77)

respectively where the amplitude of the term is related to the usual isophote parameter a_m = _m| 1 - m²| / m b for a lens with Einstein radius b. A typical early-type galaxy might have | a₄| ~ 0.01, so their fractional effect on the deflections, |₄| / b ~ | a₄| / 4 ~ 0.003, will be comparable to the astrometric measurement accuracy.