


B.4.5. Constraining Angular Structure
The angular structure of lenses is usually simply viewed as an obstacle to understanding the monopole. This is a serious mistake. The reason angular structure is generally ignored is that the ability to accurately constrain the angular structure of the gravitational field is nearly unique to gravitational lensing. Since we have not emphasized the ability of lenses to measure angular structure and other methods cannot do so very accurately, there has been little theoretical work on the angular structure of galaxies with dark matter. Both theoretical studies of halos and modelers of gravitational lenses need to pay more attention to the angular structure of the gravitational potential.
We start by analyzing a simple two-image lens using our non-parametric
model of the monopole (Eqn. B.67) in an external shear (Eqn. B.51). The
two images are located at
 A =
A =
 A(cos
A(cos
 A, sin
A, sin
 A), and
A), and
 B =
B =
 B(cos
B(cos
 B, sin
B, sin
 B) as illustrated
in Fig. B.20. To illustrate
the similarities and differences between shear and convergence, we will
also include a global convergence
B) as illustrated
in Fig. B.20. To illustrate
the similarities and differences between shear and convergence, we will
also include a global convergence
 0 in the
model. This corresponds to adding a term to the lens potential of the form
(1/2)
0 in the
model. This corresponds to adding a term to the lens potential of the form
(1/2) 0
0
 2.
The model now has five parameters - two shear components, the mass
and surface density of the monopole model and the additional global
convergence. We have only two astrometric constraints, and so can solve
for only two of the five parameters. Since the enclosed mass is always
an interesting parameter, we can only solve for one of the two shear
components. In general, we will find that the amplitude of
2.
The model now has five parameters - two shear components, the mass
and surface density of the monopole model and the additional global
convergence. We have only two astrometric constraints, and so can solve
for only two of the five parameters. Since the enclosed mass is always
an interesting parameter, we can only solve for one of the two shear
components. In general, we will find that the amplitude of
 c
depends on the amplitude of
c
depends on the amplitude of
 s.
There is, however, a special choice of the shear axis,
s.
There is, however, a special choice of the shear axis,

 =
(
=
( A +
A +
 B) / 2 +
B) / 2 +
 / 4, such
that the shear parameters become independent of each other. This allows
us to determine the "invariant" shear associated with the images,
/ 4, such
that the shear parameters become independent of each other. This allows
us to determine the "invariant" shear associated with the images,
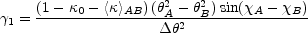 |
(B.78) |
where 
 =
|
=
| A
-
A
-  B|
is the image separation.
The monopole mass and the other shear component are degenerate,
B|
is the image separation.
The monopole mass and the other shear component are degenerate,
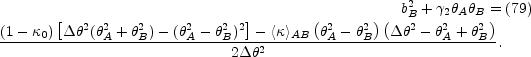 |
(B.79) |
Several points are worth noting. First, the amplitude of the invariant shear
 1
has the same degeneracy with the (local) surface density between the images
<
1
has the same degeneracy with the (local) surface density between the images
< >AB as
it does with a global convergence
>AB as
it does with a global convergence
 0. More centrally
concentrated mass distributions with lower
<
0. More centrally
concentrated mass distributions with lower
< >AB
require higher external
shears to fit the same data. Second, the other component
>AB
require higher external
shears to fit the same data. Second, the other component
 2
introduces an uncertainty into the enclosed mass, with a series of
somewhat messy trade offs between bB2,
2
introduces an uncertainty into the enclosed mass, with a series of
somewhat messy trade offs between bB2,
 2,
<
2,
< >AB
and
>AB
and  0. As a
practical matter,
the shear does not lead to an astronomically significant uncertainty in
the mass, since
0. As a
practical matter,
the shear does not lead to an astronomically significant uncertainty in
the mass, since
 2
2
 0.1 in all but
the most extreme situations.
0.1 in all but
the most extreme situations.
The external shear is only one component of the quadrupole. There is also an
internal shear due to the mass interior to the images (Eqn. B.52).
The internal and external shears differ in their "handedness". For the same
angular deflection
(d /
d
/
d ) they
have opposite signs for the radial deflection
(d
) they
have opposite signs for the radial deflection
(d /
d
/
d ). The solution
for two images is much the same as for an external shear. There is an
invariant shear component, whose amplitude scales with
1 -
). The solution
for two images is much the same as for an external shear. There is an
invariant shear component, whose amplitude scales with
1 -  0 -
<
0 -
< >AB
but whose orientation differs from that
of the external shear solution. The monopole mass
bB2 is degenerate with the
>AB
but whose orientation differs from that
of the external shear solution. The monopole mass
bB2 is degenerate with the
 2
shear component and the
2
shear component and the
 0 and
<
0 and
< >AB
surface
densities. The actual expressions are too complex to be illuminating.
>AB
surface
densities. The actual expressions are too complex to be illuminating.
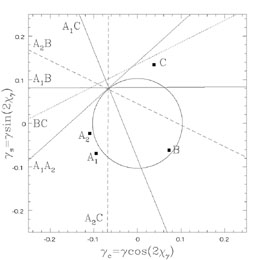
Fig. B.23 illustrates how the invariant shears
combine to determine
the overall structure of the quadrupole for the lens PG1115+080.
For each image pair there is a line of permitted shears because of the
degeneracy between the enclosed mass and the second shear component. The
invariant shear component is the shear at the point where the line passes
closest to the origin. If the quadrupole model is correct, the lines for
all the image pairs will cross at a point, while if it is incorrect they
will not. PG1115+080 is clearly going to be well modeled if
the quadrupole
is dominated by an external shear and poorly modeled if it is dominated by
an internal shear. This provides a simple geometric argument for why full
models of PG1115+080 are always dominated by an external shear
(e.g. Impey et al.
[1998]).
A failure of the curves to cross in both cases is primarily evidence for a
mixture of external and internal quadrupoles or the presence of other
multipoles
rather than for a problem in the monopole mass distribution. In
Fig. B.23
we used an SIS for the monopole. For a point mass monopole, the figure
looks almost the same provided we expand the scale - the invariant shear
scales as
1 - < >AB
so in going from a SIS with
1 - <
>AB
so in going from a SIS with
1 - < >AB
>AB
 1/2
to a point mass with
1 - <
1/2
to a point mass with
1 - < >AB
= 1 the shear will double.
>AB
= 1 the shear will double.
 |
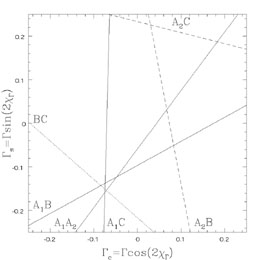 |
Figure B.23. The invariant shears for the lens PG1115+080 modeled using either an external (top) or an internal (bottom) quadrupole and an SIS monopole. Each possible image pair among the A1, A2, B and C images, constrains the quadrupole to lie on the labeled line. The amplitude and orientation of each invariant shear is given by the point where the corresponding line passes closest to the origin. Models of PG1115+080 show that the quadrupole is dominated by external (tidal) shear. Here we see that for the external quadrupole (top), the lines nearly cross at a point, so the data are consistent with an almost pure external shear. For an internal quadrupole (bottom), the A2B and A2C image pairs require shear parameters completely inconsistent with the other images. |
This scaling of the quadrupole with the surface density of the monopole provides an as yet unused approach to studying the monopole. Since the mass enclosed by the Einstein radius is nearly constant, the more centrally concentrated constant mass-to-light (M / L) ratio models must have lower surface mass densities near the images than the SIE model. As a result, they will require quadrupole amplitudes that are nearly twice those of models like the SIS with nearly flat rotation curves. Since the typical SIE model of a lens has an ellipticity that is comparable to the typical ellipticities of the visible galaxies, the more centrally concentrated monopole of a constant M / L model requires an ellipticity much larger than the observed ellipticity of the lens galaxy. The need to include an external tidal shear to represent the environment allows these models to produce acceptable fits, but the amplitudes of the required external shears are inconsistent with expectations from weak lensing (Part 3).