B.5. TIME DELAYS

Nothing compares to the measurement of the Hubble constant in bringing out the worst in astronomers. As we discussed in the previous section on lens modeling, many discussions of lens models seem obfuscatory rather than illuminating, and the tendency in this direction increases when the models are used to estimate H₀. In this section we discuss the relationship between time delay measurements, lens models and H₀. All results in the literature are consistent with this discussion, although it may take you several days and a series of e-mails to confirm it for any particular paper. The basic idea is simple. We see images at extrema of the virtual time delay surface (e.g. Blandford & Narayan [1986], Part 1) so the propagation time from the source to the observer differs for each image. The differences in propagation times, known as time delays, are proportional to H₀^-1 because the distances between the observer, the lens and the source depend on the Hubble constant (Refsdal [1964]). When the source varies, the variations appear in the images separated by the time delays and the delays are measured by cross-correlating the light curves. There are recent reviews of time delays and the Hubble constant by Courbin, Saha & Schechter ([2002]) and Kochanek & Schechter ([2004]). Portions of this section are adapted from Kochanek & Schechter ([2004]) since we were completing that review at about the same time as we presented these lectures.

To begin the discussion we start with our standard simple model, the circular power law lens from Section B.3. As a circular lens, we see two images at radii _A and _B from the lens center and we will assume that _A > _B (Fig. B.20). Image A is a minimum, so source variability will appear in image A first and then with a time delay t in the saddle point image B. We can easily fit this data with an SIS lens model since (see Eqn. B.21 and B.22) to find that _A = + b and _B = b - where b = (_A + _B) / 2 is the critical (Einstein) radius of the lens and = (_A - _B) / 2 is the source position. The light travel time for each image relative to a fiducial unperturbed ray is (see Part 1)

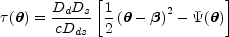(B.93)

where the effective potential = b for the SIS lens. Remember that the distances are comoving angular diameter distances rather than the more familiar angular diameter distances and this leads to the vanishing of the extra 1 + z_l factor that appears in the numerator if you insist on using angular diameter distances. The propagation time scales as H₀^-1 10h^-1 Gyr because of the H₀^-1 scalings of the distances. After substituting our lens model, and differencing the delays for the two images, we find that

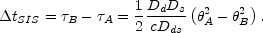(B.94)

The typical deflection angle b ~ 3 × 10^-6 radians (so R_A² ~ 10^-11) converts the 10h^-1 Gyr propagation time into a time delay of months or years that can be measured by a graduate student. Naively, this result suggests that the problem of interpreting time delays to measure H₀ is a trivial problem in astrometry.

We can check this assumption by using our general power-law models from Section B.3 instead of an SIS. The power-law models correspond to density distributions r^-n, surface densities R^1-n and circular velocities v_c r^{(2-n) / 2} of which the SIS model is the special case with n = 2. These models have effective potentials

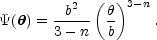(B.95)

As we discussed in the Section B.4.1 we can fit our simple, circular two-image lens with any of these models to determine b(n) and (n) (Eqn. B.66), which we can then substitute into the expression for the propagation time to find that the time delay between the images is

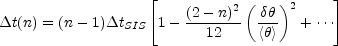(B.96)

where we have expanded the result as a series in the ratio between the mean radius of the images <> = (_A + _B) / 2 and the thickness of the radial annulus separating them = _A - _B. While the expansion assumes that / <> ~ / b is small, we can usually ignore higher order terms even when / <> is of order unity. We now see that the time delay depends critically on the density profile, with more centrally concentrated mass distributions (larger values of n) producing longer time delays or implying larger Hubble constants for a fixed time delay.

The other idealization of the SIS model, the assumption of a circular lens, turns out to be less critical. A very nice analytic example is to consider a singular isothermal model with arbitrary angular structure in which = bF() / 2 where F() is an arbitrary function of the azimuthal angle. The singular isothermal ellipsoid (Eqn. B.37) is an example of this class of potential. For this model family, t = t_SIS independent of the actual angular structure F() (Witt, Mao & Keeton [2000]).