


B.6.7. Cosmology With Lens Statistics
The statistics of lenses, in the sense of the number of lenses expected
in a sample of sources as a function of cosmology, is a volume test of
the cosmological model because the optical depth (at least for flat
cosmologies) is proportional to
Ds3. However, the number of lenses also
depends on the comoving density
and mass of the lenses (n*,
 *
and
*
and  in the simple SIS
model). While n* could plausibly be estimated
locally, the
in the simple SIS
model). While n* could plausibly be estimated
locally, the
 *4
dependence on the mass scale makes it very difficult to use local
estimates of galaxy kinematics or masses to normalize the optical depth.
The key step to eliminating this problem is to note that there is an
intimate
relation between the cross section, the observed image separations and the
mass scale. While this will hold for any mass model, the SIS model is the
only simple analytic example. The mean image separation for the lenses
should be
independent of the cosmological model for flat cosmologies (and only weakly
dependent on it otherwise). Thus, in any lens sample you can eliminate the
dependence on the mass scale by replacing it with the observed mean image
separation,
*4
dependence on the mass scale makes it very difficult to use local
estimates of galaxy kinematics or masses to normalize the optical depth.
The key step to eliminating this problem is to note that there is an
intimate
relation between the cross section, the observed image separations and the
mass scale. While this will hold for any mass model, the SIS model is the
only simple analytic example. The mean image separation for the lenses
should be
independent of the cosmological model for flat cosmologies (and only weakly
dependent on it otherwise). Thus, in any lens sample you can eliminate the
dependence on the mass scale by replacing it with the observed mean image
separation,  SIS
SIS
 n*
<
n*
<
 >2
Ds3.
Full calculations must include corrections for angular selection effects.
Most odd results in lens cosmology arise in calculations that ignore the
close coupling between the image separations and the cross section.
>2
Ds3.
Full calculations must include corrections for angular selection effects.
Most odd results in lens cosmology arise in calculations that ignore the
close coupling between the image separations and the cross section.
In practice, real calculations are based on variations of the maximum likelihood method introduced by Kochanek ([1993b], [1996a]). For each lens i you compute the probability pi that it is lensed including magnification bias and selection effects. The likelihood of the observations is then
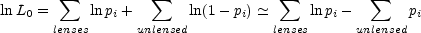 |
(B.119) |
where ln(1 - pi)
 - pi
provided pi << 1. This simply encodes the
likelihood of finding the observed number of lenses given the individual
probabilities that the objects are lensed. Without further information,
this likelihood could determine the limits on the cosmological model
only to the extent we had accurate prior estimates for
n* and
- pi
provided pi << 1. This simply encodes the
likelihood of finding the observed number of lenses given the individual
probabilities that the objects are lensed. Without further information,
this likelihood could determine the limits on the cosmological model
only to the extent we had accurate prior estimates for
n* and
 *.
*.
If we add, however, a term for the probability that each detected lens has its observed separation (Eqn. B.112 plus any selection effects)
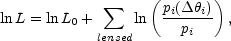 |
(B.120) |
then the lens sample itself can normalize the typical mass scale of the
lenses (Kochanek
[1993b]).
This has two advantages. First, it eliminates any systematic
problems arising from the dynamical normalization of the lens model and its
relation to the luminosity function. Second, it forces the cosmological
estimates from the lenses to be consistent with the observed image
separations - it makes no sense to produce cosmological limits that
imply image separations
inconsistent with the observations. In theory the precision exceeds that
of any local calibration very rapidly. The fractional spread of the
separations about the mean is ~ 0.7, so the fractional uncertainty in
the mean separation scales as
0.7 / N1/2 for a sample of N lenses. Since the
cross section goes as the square of the mean separation, the uncertainty
in the mean cross section
1.4 / N1/2 exceeds any plausible accuracy of a local
normalization for
 *
(10% in
*
(10% in
 *,
or 20% in <
*,
or 20% in < >
>

 *2,
or 40% in
*2,
or 40% in 

 *4) with only
N
*4) with only
N  10 lenses.
10 lenses.
Any other measurable property of the lenses can be added to the likelihood, but the only other term that has been seriously investigated is the probability of the observed lens redshift given the image separations and the source redshift (Kochanek [1992a], [1996a], Helbig & Kayser [1996], Ofek, Rix & Maoz [2003]). In general, cosmologies with a large cosmological constant predict significantly higher lens redshifts than those without, and in theory this is a very powerful test because of the exponential cutoff in Eqn. B.114. The biggest problem in actually using the redshift test, in fact so big that it probably cannot be used at present, is the high incompleteness of the lens redshift measurements (Section B.2). There will be a general tendency, even at fixed separation, for the redshifts of the higher redshift lens galaxies to be the ones that are unmeasured. Complete samples could be defined for a separation range, usually by excluding small separation systems, but a complete analysis needs to include the effects of groups and cluster boosting image separations beyond the splitting produced by an isolated galaxy. For example, how do we include Q0957+561 with its separation of 6."2 that is largely due to the lens galaxy but has significant contributions from the surrounding cluster?