2. The mass and size of galaxies

A striking result of our rotation curve analysis is that most rotation curves decline slowly, if at all, and none of them reaches a Keplerian drop off in the outer parts. This raises the problem of the extent of a galaxy: does the mass continue to increase outwards or does it stop somewhere? A related question is: how is the mass distributed? If all the mass is in a disk its stability is in question. Ostriker and Peebles (1973) have proposed that a dynamically hot component may exist which stabilizes the disk; this component may be distributed in a halo. Such a massive halo might dominate the gravitational potential field in the outer parts of a galaxy. If these haloes exist then our mass models are clearly wrong, since they are based on the thin disk approximation. The curves of M(R), however, will change by at most 50% if we assume that all the mass is in a sphere (cf. Krumm and Salpeter, 1977). Ostriker, Peebles and Yahil (1974) have discussed the possibility that these haloes may be about ten times as massive as the disk and extend out to 0.3-0.5 Mpc. For spiral galaxies with such haloes the mass-to-luminosity ratio has to be in the order of 100. Various lines of argument seem to indicate that there is indeed a great amount of mass at large distances from the centre of galaxies. Most of the evidence comes from statistical studies i.e. binary galaxy statistics (Turner, 1976), the argument that the Local Group is stable (Kahn and Woltjer, 1959) and considerations about the orbits of satellite galaxies around our own Galaxy (e.g. Lin and Lynden-Bell, 1977).

Our results on masses of individual galaxies can now be compared with the other determinations of M(R). In Fig. 1 we present a plot of log M vs log R, similar to that of Turner and Ostriker (1977). We have used their values on the Local Group mass, and their results of the binary statistics, corrected to H_o = 75 km s^-1 Mpc^-1. We have also included the value derived by Van Albada and Freeman (1978) for the pure spiral pairs in Turner's sample (Turner, 1976). For our Galaxy we show our mass model in the inner parts, and data derived from the motions of satellites around our Galaxy (Globular Clusters: Hartwick and Sargent, 1978; Magellanic, Clouds: Lin and Lynden-Bell, 1977; Dwarf Ellipticals: Turner and Ostriker, 1977). For the galaxies NGC 2841, NGC 5055 and NGC 3198 we give log M(R) and for the other galaxies in our sample we have plotted log M(R_o), where R_o is the radius of the last measured point on the rotation curve.

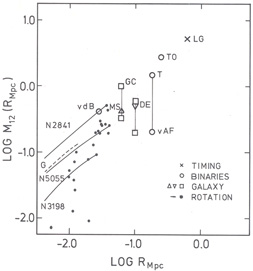Figure 1. Masses (units 1012 M) of spiral galaxies within a distance R (unit Mpc) from the centre, scaled to a Hubble constant of 75 km s-1 Mpc-1. The cross refers to the mass of the Local Group derived from the timing argument (Ostriker et al., 1973). Circles refer to binary galaxy statistics (T: Turner, 1976; TO: Turner and Ostriker, 1977; vAF: Van Albada and Freeman, 1978; vdB: Ostriker et al.'s value from Van den Bergh's sample). Squares and triangles refer to the mass of our galaxy inferred from satellites ( Hartwick and Sargent, cf. Sargent 1977; Lin and Lynden-Bell, 1977; Turner and Ostriker, 1977). Dots represent values of M(Ro) for the galaxies in our sample; the thin lines are curves of M(R) for individual galaxies.

For each galaxy M is roughly proportional to R, but for different galaxies we find curves with a different zero point. This difference is proportional to V² where V is a measure of the rotation speed of a galaxy. As a convenient measure of this speed we have calculated a surface density weighted mean velocity at R = R_o, that is V_m = (2E_o / M_o)^1/2, with E_o is the value of the kinetic energy of rotation (chapter 6.3) at R_o. The value of V_m does not depend much on the choice of R_o: the curve of V_m(R) = (2E(R) / M(R))^1/2 is roughly constant in the interval 1/2R_o to R_o. We use this quantity rather than the maximum rotational velocity, V_max, because for most galaxies the rotation curve varies somewhat irregularly with radius, V_max is then not a representative value. It is not so surprising that we find a scaling of the log M - log R curves with V_m²: in all the calculations of masses the basic assumption is the balance of forces between the gravitational force and the centrifugal force: GM / R² ~ V² / R; hence M ~ V²R. Therefore, if we have to compare the results of our models with those from statistical studies we have to know the value of V_m for the galaxies under consideration (cf. Burbidge, 1975). The galaxies in Fig. 1 have the following V_m values: NGC 2841 V_m = 273.0 km s^-1; NGC 5055 V_m = 199.3 km s^-1 and NGC 3198 V_m = 140.0 km s^-1. The different zero points in Fig. 1 are consistent with these V_m values. For our Galaxy V_m = 232.5 km s^-1, but this value is not well determined because of the uncertainties in the galactic rotation curve beyond the solar distance. The values of the mass of our Galaxy derived from the motions of the satellites are all compatible with the straight-line extrapolation from our model, except perhaps the values for globular clusters in case these have an isotropic velocity distribution (the upper square; the lower square is one for a radial velocity distribution). This may indicate that the Galaxy has a flat rotation curve or higher rotational velocities than we used. We will discuss the results from the binary galaxies in the next section, since these are based on M / L ratios.

It is difficult to determine the size of a galaxy, or to estimate where the contribution of the outer shells of the mass distribution to the rotation curve becomes negligible. In the determination of the mass surface density, _M(r), the contributions of these shells have been estimated with a rotation law which lies in between a Keplerian curve and a flat curve beyond the radius of the last measured point, R_o (see chapter 6). This means that R_o plays an essential role in the curves of _M(r), and since R_o has been determined from the 21-cm line data it is clear that the sensitivity of the HI observations is essential too. In most cases R_o refers to the radius where the column density of neutral hydrogen is about 10²⁰ atoms cm^-2. In the galaxies with large scale asymmetries we have excluded the asymmetric outer regions, and R_o for these galaxies is consequently smaller than it would have been if no asymmetry was present. A more serious problem is the treatment of galaxies which are thought to be warped. The warp problem is not understood, but there is as yet no contradiction in the existence of massive haloes around warped galaxies. Moreover, not only warped galaxies have a more or less flat rotation curve in the outer parts, also a few of the galaxies which are thought to have oval distortions in the plane of the disk (see chapter 5) have flat rotation curves.

We have estimated the minimum amount of mass beyond R_o from the comparison of the results of our model fits with those of Nordsieck's inversion procedure (see chapter 6). In Fig. 2b we have plotted the ratio of M_o, the mass at R = R_o from Nordsieck's method, and M_f, the total mass in the model fits, as function of V_m. This ratio is about 0.5 for most of the galaxies, independent of V_m. Thus for most galaxies at least half of the mass resides outside the last measured point on the rotation curve. We will discuss the consequences of this result on the mass-to-luminosity ratio in the next section.

Figure 2. a Blue luminosity (units 109 L) vs mean rotation velocity as defined in text. b Ratio of the mass Mo, at radius Ro, derived with Nordsieck's method and Mf, the mass in the model fits, vs. mean rotation velocity.

We have investigated a few correlations between V_m, R_o and other quantities. In Fig. 2a we have plotted the blue luminosity against V_m for the galaxies in our sample. We find a correlation between these quantities. This correlation is similar to the one found by Tully and Fisher (1977) between the width of the integral HI profile and the luminosity. Another correlation is the one between M(R_o) and R_o, as can be seen in Fig. 1. In Fig. 3 we have plotted a few variants of this correlation i.e. between V_m and the radius where _M(R) = 50 M pc^-2, and between V_m and A₃ where A₃ is the scale size of the Toomre disk in the model fits. R( = 50) and A₃ have more physical significance than R_o, but are still not free of selection effects. The correlation between V_m and R( = 50) is fairly good except for M81, M51, M101 and NGC 4736. The correlation between V_m and A₃ is less impressive but also here the points in the lower right corner come from galaxies with high V_m and small R_o. In Fig. 4 we present plots of the cumulative angular momentum at R_o, H_o and of cumulative kinetic energy of rotation at R_o, E_o, both as function of M_o. Here we find correlations with small intrinsic scatter. These correlations can be explained in terms of the correlation between V_m and a scale size R_s: we find that log R( = 50) = 0.64 log V_m + const. and log M_o log R_o^2.25; since E ~ V⁴R, H ~ V³ R² and M ~ V²R we have V ~ M^0.28, R_s ~ M^0.44, H ~ M^1.72 and E ~ M^1.56. The question is whether such correlations are relevant: if the scale size R_s, be it R( = 50) or R_o, is determined in such a way that it roughly correlates with V_m then the other correlations follow. At present it is not clear whether the correlation between V_m and R_s is intrinsic or not. Note, however, that the galaxies in our sample are in a certain sense selected on their mean optical brightness (because they appear in the Reference Catalogue of Bright Galaxies) and the low-luminosity galaxy NGC 3109 does not follow the trend (cf. Fig. 3b). We will take up the size problem again in sections 5 and 6, but we point out here that it is very difficult to find a definition of the size R_s which is satisfactory. For that reason we have listed various size-definitions: R_o, R( = 50), and the optical size, R(), from De Vaucouleurs et al. (1976) in Table 1.

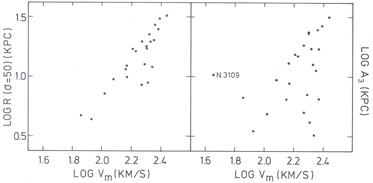Figure 3. a Radius at which the surface density (from Nordsieck's method) is 50Mo pc-2 vs mean rotation velocity. b Scalelength of the fitted Toomre nT = 1 disk vs mean rotation velocity.

Figure 4. a Angular momentum Ho (units 1013 M kpc km s-1) vs mass Mo (units 1010 M), both within the radius of the last measured point Ro. b Kinetic energy of rotation Eo (within Ro; units 1014 M km2 s-2) vs Mo.

Table 1.

Galaxy	LB†	(B - V)0	M0 / LB	Mf / LB	M0 / Mf	R(0)†	R( = 50)/R(0)	Ro/R(0)
	(109 L)					kpc
N3718
M81	19.9	0.81	4.92	5.78	0.85	10.6	1.12	1.23
N4151	13.2	0.67	5.76	12.1	0.48	11.0	1.10	1.78
N4736	19.8	0,69	2.68	4.49	0.60	9.14	0.93	1.09
M31	25.9	0.74	11.4	20.2	0.56	14.2	1.75	2.08
N891	32.9	0.68	5.99	11.0	0.55	18.7	1.04	1.26
N2841	17.7	0.73	28.1	70.1	0.40	8.85	3.63	4.08
N4565	53.5	0.64	8.19	16.9	0.48	23.4	1.28	1.64
N5383	28.0	0,57	7.36	17.7	0.42	15.4	1.16	1.74
N4258	27.0	0.56	7.22	15.2	0.48	14.5	1.34	2.04
N5055	25.5	0.64	9.92	15.9	0.62	12.8	1.36	3.21
M51	49.8	0.52	1.43	2.37	0.60	14.1	0.62	0.84
N7331	45.7	0.64	6.87	18.2	0.38	17.3	1.55	1.75
N253
N3198	7.9	0.42	11.6	13.0	0.87	9.06	1.28	2.84
N3359
N5033	24.7	0.44	10.9	17.9	0.61	18.6	1.21	1.92
N5907	18.3	0.56	14.4	19.5	0.74	13.0	1.55	2.36
N7640
N300
M33	2.6	0.44	2.88	8.08	0.36	5.76	0.76	0.94
I342	17.1		7.54	15.2	0.50	10.4	1.56	2.19
N2403	7.5	0.37	4.93	13.6	0.36	7.49	1.25	1.56
N4244	2.6	0.24	10.3	15.4	0.68	5.48	1.31	2.24
M83	85.3		2.22	2.86	0.77	14.2	1.18	2.71
M101	50.4	0.40	1.96	3.79	0.52	28.2	0.45	0.48
N6946
N2805
N4631	26.2	0.37	1.60	4.01	0.40	7.92	1.24	1.25
N4236	2.9	0.25	4.48	9.66	0.46	6.99	0.67	1.67
I2574
N3109	1.3		7.00	13.9	0.51	3.28	-	6.22
HoII
N4449
Galaxy	-
From BTo and D(0) given by De Vaucouleurs et al. (1976) and the assumed distance.
R0 is the radius of the last measured point on the rotation curve.
R( = 50) is the radius where the mass surface density equals 50 M pc-2.