6. EVOLUTIONARY MODELS: STAR-FORMING GALAXIES

6.1. Star-forming, normal and sub-mm galaxies

The radio emission of star-forming galaxies correlates with their star formation rate, as demonstrated by the well-established tight correlation with far-IR emission (Helou et al. 1985, Gavazzi et al. 1986, Condon 1992, Garrett 2002). Yun et al. (2001) found that the overall trend in the range L(60 µm) 10³⁰ - 10^32.5 erg s^-1 Hz^-1 is indistinguishable from a linear relation:

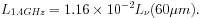(14)

Galaxies with L(60 µm) < 10³⁰ erg s^-1 Hz^-1 are found to have radio to far-IR luminosity ratios systematically lower than those given by eq. (14). The apparent deviation from linearity in the radio/far-IR correlation at low luminosities is supported by a comparison of 60 µm and 1.4 GHz local luminosity functions (Yun et al. 2001, Best et al. 2005). Simply shifting the 60 µm luminosity function (Saunders et al. 1990, Takeuchi et al. 2003) along the luminosity axis according to eq. (14) yields a good match to the radio luminosity function (Best et al. 2005, Mauch & Sadler 2007) for L_{1.4 GHz} 10²⁸ erg s^-1 Hz^-1. At yet lower luminosities, however, the extrapolated luminosity function lies increasingly above the observed one. Full agreement is recovered (Fig. 8) by replacing eq. (14) with

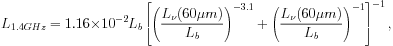(15)

in which L_b = 8.8 × 10²⁹ erg s^-1 Hz^-1.

While a radio/far-IR correlation is expected since young stars are responsible both for dust heating and for the generation, via supernova explosions, of synchrotron emitting relativistic electrons, a clear explanation of its tightness and of its linearity over a large luminosity range is still missing. A decrease of the L_{1.4 GHz} / L(60 µm) ratio with increasing far-IR luminosity is expected from the increase of the effective dust temperature, T_d, with luminosity (Blain & Longair 1996). For a galaxy like the Milky Way, the far-IR SED peaks at 170 µm, whereas for an Ultra Luminous Infrared Galaxy (ULIRG) it peaks at about 60 µm (Lagache et al. 2005). This factor of 3 increase in temperature for a factor ~ 10³ increase in luminosity corresponds to T_d L_FIR^1/6. If the radio luminosity is proportional to the global far-IR luminosity, this increase in dust temperature results in a decrease of the L_{1.4 GHz} / L(60 µm) ratio by a factor of 2.5-3.

On the other hand, there are different contributions to the global far-IR luminosity. In Luminous and Ultra Luminous Infrared galaxies, the emission is dominated by warmer dust, associated with star-formation, while infrared "cirrus" emission, heated by older stars, becomes increasingly important in galaxies with lower and lower star-formation rates. The latter component may be weakly correlated with radio emission, if at all. Moreover, in very low luminosity galaxies interstellar magnetic fields may be so weak as to let synchrotron emitting electrons escape into intergalactic space or to lose energy primarily via inverse Compton scattering of CMB photons. These processes may over-compensate the effect of decreasing dust temperature ⁵.

Anyway, the tight empirical relationship between radio and far-IR luminosities for star-forming galaxies allows us to take advantage of the wealth of data at far-IR/sub-mm wavelengths to derive the radio evolution properties. We expect a different evolution for starburst and normal late-type galaxies as the starburst activity is likely triggered by interactions and mergers that were more frequent in the past, while in normal galaxies the star-formation rate has probably not changed much over their lifetimes. The bulk of the sub-mm counts measured by SCUBA surveys (Scott et al. 2006, Coppin et al. 2006) is due to yet another population, the sub-mm galaxies (SMGs), proto-spheroidal galaxies in the process of forming most of their stars (Granato et al. 2004).

There have been a number of attempts to model the evolution of star-forming galaxies and in particular to account for the apparent intrusion of this population into the source counts at S_{1.4 GHz} 1 mJy; see e.g. King & Rowan-Robinson (2004). A straightforward extrapolation to radio frequencies of the evolutionary models by Negrello et al. (2007) for the three populations (normal, starburst and sub-mm galaxies), exploiting eq. (15) and the SEDs of NGC 6946 for normal late-type galaxies and of Arp220 for starburst and proto-spheroidal galaxies, yields the curves shown in Figs. 4 - 6, nicely reproducing the counts at tens of µJy levels. We note however that new observational data, some of which is described in Section 2.3, may permit substantial refinement of these models.

The cross-over between synchrotron plus free-free emission prevailing at cm wavelengths, and thermal dust emission, generally occurs at 2-3 mm (in the rest frame), so that at frequencies of tens of GHz there are contributions from both components (see De Zotti et al. 2005).

6.2. Radio afterglows of -ray bursts (GRBs)

The afterglow emission of GRBs can be modelled as synchrotron emission from a decelerating blast wave in an ambient medium, plausibly the interstellar medium of the host galaxy (Waxman 1997, Wijers & Galama 1999, Mészáros 1999). The radio flux above the self-absorption break at 5 GHz, is proportional to ^1/3 up to a peak frequency that decreases with time. This implies that surveys at different frequencies probe different phases of the expansion of the blast wave. Owing to their high brightnesses, GRB afterglows may be detected out to exceedingly high redshifts and are therefore important tracers of (a) the early star formation in the Universe, and of (b) the absorption properties of the intergalactic medium across the reionization phase. Estimates of the counts of GRB afterglows have been made by Ciardi & Loeb (2000), who found that at a fixed time-lag after the GRB in the observer's frame, there is only a mild change in the observed flux density at radio wavelengths with increasing redshift. This stems in part from the fact that afterglows are brighter at earlier times and that a given observed time refers to an intrinsic time in the source frame that is earlier as the source redshift increases. According to Ciardi & Loeb (2000) estimates, a large area survey at 1 cm to a flux limit 1 mJy should discover some GRBs (see also Seaton & Partridge 2001, De Zotti et al. 2005). Predictions of Ciardi & Loeb's models at 1.4 and 3 GHz are shown in Figs. 5 and 6.

⁵ We are grateful to J. Condon for enlightening comments on this issue. Back.