1. INTRODUCTION

1.1. Motivation

Open your window and take a look at the night sky on a clear night. You can see lots of stars, lots of different types of stars. You work in astrophysics so you can count the stars and measure their light (you can use different photometric filters or measure spectra), sum the individual observations, and obtain the integrated luminosity (magnitudes or spectra). After that, ask some colleagues to do the same experiment, observing the same number of stars, , you have counted in distant places, let us say n_sam colleagues. In fact, they will see different regions of the sky so they will observe different stars; hence, you are sampling the sky with n_sam elements, each with stars. Compare the integrated luminosities and, almost certainly, they will differ. But you are looking in the Sun's neighbourhood where you can define the set of physical conditions that define the stars that you would observe (initial mass function, star formation history, age, metallicity); hence, your results and those of your colleagues should be consistent with these physical conditions, although they differ from each other, right?

Now take your favourite synthesis code, include the physical conditions, and obtain the integrated luminosity, magnitude, and spectra. In addition, perform millions (n_sam is millions) of Monte Carlo simulations with those physical conditions using stars in each simulation. Almost certainly, neither the integrated luminosities obtained by the code nor any of those obtained by Monte Carlo simulations equal the ones you or any of your colleagues have obtained. However, such scatter is an inherent result of nature and, as it should be, is implicit in the modelling. Therefore, you see scatter in both observations by you and your colleagues and the Monte Carlo simulations; but where is the scatter in the standard results provided by synthesis codes? After all, most codes only produce a single result for given physical conditions.

After some time thinking about this (several years in my case), you realize that the results of the Monte Carlo simulations are distributed, and you can glimpse the shape of such distributions. Moreover, you realize that your observations are inside the distribution of the Monte Carlo results once binned. Maybe they are not in the most populated bin, maybe some of them are in a low-frequency bin, but they are inside the distribution of simulations, exactly as if they were additional simulations. You then obtain the mean value of the distribution and you realize that it is suspiciously similar to the value obtained by the synthesis code using as a scaling factor. It is also applied to the mean value obtained from your observational set. Furthermore, if you obtain the variance (a measure of scatter) for the Monte Carlo set and the observational set and divide them by the mean values you obtained before, the results are similar to each other and to the (so-called) surface brightness fluctuations, SBF, the synthesis code would produce. It is valid for = 1 and = ∞, although the larger that n_sam is, the more similar the results are.

From this experiment you realize that the shape of the integrated luminosity distribution changes with and would actually be power law-like, multimodal, bimodal, or Gaussian-like, but synthesis models, the standard synthesis models you have known for years, always produce the correct mean value of the simulation /observational set. Standard models are also able to obtain a correct measure of the dispersion of possible results (some codes have actually computed it since the late 1980s). A different issue is that most standard synthesis models provide only the mean value of the distribution of possible luminosities; hence, they lose part of their predicting power.

If you perform this experiment using different photometric filters or integrated spectra, you also realize that, depending on the wavelength, you obtain different values of the mean and the variance. You will certainly find that the scatter is greater for red than for blue wavelengths. But this result is consistent with the SBF values obtained from the population synthesis code, which does not include observational errors, so such variation in the scatter with wavelength is a physical result valid for = 1 and = ∞. This is somewhat confusing since it implies that knowledge of the emission in a spectral region does not directly provide knowledge regarding other spectral regions. There is no perfect correlation between different wavelengths, only partial correlations. You might then think that a ² fitting including only the observational error and not the theoretical scatter might not be very good; it might be better to include the physical dispersion obtained from the models. It would be even better to include the theoretical correlation coefficients among different wavelengths.

You then realize that the meaning of sampling effects are primarily related to n_sam and only secondarily to , and you begin to think about how to take advantage of this. We know that n_sam × is the total number of stars in the system, N_tot; hence, we can establish that the analysis of resolved populations using colour-magnitude diagrams (CMDs) uses = 1 and n_sam = N_tot. In fact, CMDs are the best option for inferring stellar population parameters since you have information about all the stars and about how their luminosities are distributed. Analysis of the integrated properties of a fully unresolved system uses = N_tot and n_sam = 1. Systems that are not fully resolved or not fully unresolved are becoming the norm with new and future observational facilities; they have and n_sam values in the range 1 and N_tot. The stars are not resolved, but you have more information than only the integrated properties: you have more than one event to sample the distribution of possible luminosities. If you apply this idea to integral field units (IFUs), you realize that IFU observations (the overall set of IFU observations, not the individual observation of an IFU) can be used to sample the distribution of possible luminosities and to obtain more accurate inferences about stellar populations in the system. If you understand how the distributions of integrated luminosities vary with and the wavelength, going from power-law-like, multimodal, bimodal and Gaussian-like when increases, you can apply this to any set of systems. For instance, it can be applied to the globular cluster system and to predict , age, metallicity, and star formation history ranges, where you would observe bimodal colour distributions.

Stellar population modelling is intrinsically probabilistic by construction and is independent whether we are aware of it or not. It describes all the possible situations once physical conditions and the number of stars, , are defined. It is actually the most accurate description we have of stellar populations. Mother Nature is intrinsically stochastic, playing with the whole range of available possibilities for given physics of the system. If you realize that, you will also realize that the observed scatter (once corrected for observational errors) contains physical information, and you will look for such scatter.

The study of stochasticity in the modelling of stellar populations is not new. However, in recent years, with the increasing resolution of observational facilities, the subject has become more and more relevant. There are several papers that address partial aspects related to the stochasticity of stellar populations, but almost none that address the issue from a general point of view and exploit the implications. This last point is the objective of this paper. To achieve this, I assume that all synthesis models are equivalent and correct since comparison of synthesis model results is beyond the scope of this paper. I begin with a brief historical outline of the evolution of stellar population modelling. I continue with an analysis of the origin of stochasticity in modelling in Section 2. Parametric and Monte Carlo descriptions of stellar population modelling are presented in Sections 3 and 4, respectively. I describe the implications of stochasticity in the use of stellar population codes in Section 5. This section includes some rules of thumb for the use of synthesis models. I outline an unexplored area in which stochasticity could play a role in Section 6. My conclusions are presented in Section 7.

1.2. A short historical review

The stellar population concept can be traced back to the work of Baade (1944) through the empirical characterization of CMDs in different systems by direct star counting. Similarities and differences in star cluster CMD structure allowed them to be classified as a function of stellar content (their stellar population). Closely related to CMD studies is the study of the density distribution of stars with different luminosities (the stellar luminosity function). In fact, luminosity functions are implicit in CMDs when the density of stars in each region of the CMD is considered, that is, the Hess diagram (Hess 1924). The 3D structure provided by the Hess diagram contains information about the stellar content of the system studied.

It was the development of stellar evolution theory in the 1950s (e.g. Sandage and Schwarzschild 1952) that allowed us to relate the observed structures in CMDs to the age and metallicity of the system, and explain the density of stars in the different areas of the Hess diagram according to the lifetime of stellar evolutionary phases (and hence the nuclear fuel in each phase). CMDs are divided into the main sequence (MS) region, with hydrogen-burning stars, and post-main sequence (PMS) stars. The stellar density of MS stars in a CMD depends on the stars formed at a given time with a given metallicity. The density of PMS stars in different areas depends on the lifetime of different evolutionary phases after MS turn-off. Stellar evolution theory allows us to transform current observable quantities into initial conditions and hence provides the frequency distribution of the properties of stars at birth. This frequency distribution, when expressed in probability terms, leads to the stellar birth rate, 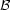(m₀, t, Z), which provides the probability that a star was born with a given initial mass, at a given time, and with a given metallicity.

By applying stellar evolution to the stellar luminosity function observed in the solar neighbourhood, Salpeter (1955) inferred the distribution of initial masses, the so-called initial mass function (IMF, (m₀)). To quote Salpeter (1955), `This luminosity function depends on three factors: (i) (m<sub>0</sub>), the relative probability for the creation of stars near m<sub>0</sub> at a particular time; (ii) the rate of creation of stars as a function of time since the formation of our galaxy; and (iii) the evolution of stars of different masses.' There are various implications in this set of assumptions that merit detailed analysis. The first is that the luminosity function used in the work is not directly related to a stellar cluster, where a common physical origin would be postulated, but to a stellar ensemble where stars would have been formed under different environmental conditions. Implicitly, the concept of the stellar birth rate is extended to any stellar ensemble, independently of how the ensemble has been chosen. The second implication is that the stellar birth rate is decomposed into two different functions, the IMF and the star formation history (SFH, (t, Z)). This is the most important assumption made in the modelling of stellar populations since it provides the definition of SFH and IMF, and our current understanding of galaxy evolution is based on such an assumption. Third, the IMF is a probability distribution; that is, the change from a (discrete) frequency distribution obtained from observations to a theoretically continuous probability distribution (among others Salpeter 1955, Mathis 1959, Scalo 1986). The direct implication of the IMF definition is that, to quote Scalo (1986), there is `no means of obtaining an empirical mass distribution which corresponds to a consistent definition of the IMF and which can be directly related to theories of star formation without introducing major assumptions.' I refer interested readers to Cerviño et al. (2013) for further implications that are usually not considered in the literature.

Following the historical developments, Hodge (1989) defined the concept of a `population box', a 3D histogram in which the x - y plane is defined by the age of the stars and their metallicity. The vertical axis denotes the number of stars in each x - y bin, or the sum of the initial masses of the stars in the bin. It is related to the star formation history, (t, Z), and, ultimately, to the stellar birth rate. Fig. 1 shows the population box for a field in the Large Magellanic Cloud disc taken from Meschin et al. (2013).

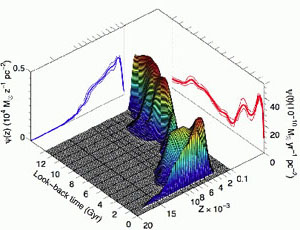Figure 1. Population box for a Large Magellanic Cloud (LMC) field taken from Meschin et al. (2013). Courtesy of C. Gallart.

A stellar ensemble with no resolved components does not provide a CMD, but the sum of all the stars in the CMD. However, we can still infer the stellar population of the system by using just this information if we can characterize the possible stellar luminosity functions that sum results in the integrated luminosity of the system. The problem of inferring the stellar content from the integrated light of external galaxies was formalized by Whipple (1935). The idea is to take advantage of different photometric or particular spectral characteristics of the stars in the different regions of a CMD and combine them in such a way that we can reproduce the observations. The only requirement is to establish, on a physical basis, the frequency distribution of the spectral types and absolute magnitudes of the stars in the CDM. Studies by Sandage, Schwarzschild and Salpeter provide the probability distribution (instead of a frequency distribution) needed for proper development of Whipple's ideas, and in the late 1960s and the 1970s, mainly resulting from the work of Tinsley (1968, 1972); Tinsley and Gunn (1976), Tinsley (1980), a framework for evolutionary population synthesis and chemical evolution models was established.

In the 1980s, there were several significant developments related to stellar populations. The first was the definition of the single-age single-metallicity stellar population (SSP) by Renzini (1981) (see also Renzini and Buzzoni 1983). An SSP is the stellar birth rate when the star formation history is a Dirac delta distribution (see Buzzoni 1989 for an extensive justification of such an approximation). In addition, an SSP is each one of the possible points in the age-metallicity plane of the population box. The second development resulted from work by Charlot and Bruzual (1991) and Bruzual and Charlot (1993) using isochrone synthesis. The density of PMS stars in an SSP depends mainly on the lifetime of each PMS phase, which is linked to the amount of fuel in the phase. In addition, all PMS stars in an SSP have a mass similar to that of the MS turn-off, m_TO. Isochrone synthesis assumes that the similar recipes used to interpolate tracks in main sequence stars (homology relations in polytropic models) are valid for PMS stars as long as interpolations are between suitable equivalent evolutionary points. Hence, each PMS phase at a given age is related to stars with initial mass m_TO + m, and the density of stars in the phase is given by the integral of the IMF over the m interval. I refer interested readers to Marigo and Girardi (2001) for additional aspects of isochrone synthesis and the lifetime of PMS phases. The connection of the SSP concept to isochrones in terms of CMD diagrams and stellar luminosity functions implies that an SSP is the set of stars defined by an isochrone including the density of stars at each point of the isochrone when weighted by the IMF.

In the 1980s there were also several advances in the study of the so-called sampling effects in population synthesis, especially in relation to the number of PMS stars in a stellar population. Barbaro and Bertelli (1977) investigated how evolutionary model results vary depending on the number of stars in a synthetic cluster. The authors reported that sampling effects originate from the way the IMF is sampled and large changes in the effective temperature of a star during the PMS evolution, when there are rapid evolutionary phases (situations in which small variations in m₀ produce wide variations in luminosity). Similar studies have been carried out by Becker and Mathews (1983), Chiosi et al. (1988), Girardi and Bica (1993), Girardi et al. (1995), Santos and Frogel (1997). A common characteristic in these studies, besides the application to LMC clusters, is the identification of sampling effects with the occurrence by number of luminous PMS stars dominating the integrated light.

From a more global perspective, Buzzoni (1989) established a direct analytical formalism to evaluate sampling effects in clusters of different sizes by defining the effective number of stars, N_eff, which contributes to the integrated luminosity ¹ (which varies with the age and wavelength considered). To do so, he assumed that the number of stars with a given mass follows a Poisson statistic; hence, dispersion of the total luminosity is the sum of the independent Poisson statistics for the number of stars with a given luminosity. Obviously, the main contribution to global dispersion of the given luminosity is caused by sparse but luminous stars. Independently, Tonry and Schneider (1988), using similar arguments about Poisson statistics, proposed the use of dispersion of the total flux of a galaxy image as a primary distance indicator (so-called surface brightness fluctuation, SBF), which is an observational quantity. In fact, N_eff and SBFs are related, as shown by Buzzoni (1993). However, we must recall that theoretical SBFs are a measure of possible fluctuations around a mean value, a more general concept than that used by Tonry and Schneider (1988).

SBFs observations are one of the smoking guns of the stochasticity of stellar populations at work in nature, and the first case to take advantage of such stochasticity to draw inferences about the physical quantities of stellar systems. Another application of SBFs is the breaking of age-metallicity degeneracy in SSP results for old ages (Worthey 1994); additional applications have been described by Buzzoni (2005).

Another aspect of SBFs is that they had been extensively studied and used in systems with old stellar populations. It would be surprising if we related stochasticity to IMF sampling: the integrated light in old stellar populations is dominated by low-mass stars, which are more numerous than high-mass ones. Hence, if stochasticity is related to the IMF alone, we would expect dispersion to fade out as a system evolves. In fact, this is an erroneous interpretation of sampling effects: as cited before, the number of stars in a given PMS phase is defined by the m interval and the size of such an interval does not depend on the IMF.

To explain stochasticity in terms of Poisson statistics was the norm in the modelling of the physical scatter of stellar populations up to 2005 (among others Lançon and Mouhcine 2000, Cerviño et al. 2001, Cerviño et al. 2002, González et al. 2004). The Poisson distribution, since it is discrete, is easily related to a natural number of stars and to interpretation of the IMF as a frequency distribution (as opposed to a probability density function). But it was modelling in the X-ray domain by Gilfanov et al. (2004) that established the key point of stochastic modelling by using the stellar luminosity function. The ideas of Gilfanov et al. (2004) were expanded to the optical domain by Cerviño and Luridiana (2006), who thereby established a unified formalism in the modelling of stellar populations that can be applied from CMDs to the integrated light of galaxies. This work showed that the Poisson statistic is invalid in so far as the total number of stars in a system are correlated to each other by the 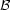(m₀, t, Z) probability distribution and introduced covariance terms in the computation of the scatter by synthesis models. Such covariance terms are especially relevant in SBF computation, as shown by Cerviño et al. (2008). That study also showed that probability distributions, when expressed as frequency distributions, follow a multinomial distribution, which is the natural result of binning of the stellar luminosity function.

In a phenomenological approach, the scatter of synthesis models has been studied in Monte Carlo simulations, particularly since the late 1990s, although previous studies can be found in the literature (e.g. Mas-Hesse and Kunth 1991, Cerviño and Mas-Hesse 1994 as well as work related to LMC clusters quoted earlier). There is a wide variety of such studies, ranging from simulations applied to specified targets or wavelength domains to general studies of Monte Carlo simulation results. Examples of specific domains include globular clusters (old populations with ~ 10⁶ stars by Yoon et al. 2006, Cantiello and Blakeslee 2007 among others), -ray and optical emission from young clusters in our galaxy (Cerviño et al. 2000b, Knödlseder et al. 2002, Voss et al. 2009) and the study of SBF (Brocato et al. 1998, Raimondo et al. 2005). Examples of general studies include work by Brocato et al. (1999), Bruzual (2002), Bruzual and Charlot (2003), Cerviño and Luridiana (2006), Fouesneau and Lançon (2010), Popescu and Hanson (2009), Piskunov et al. (2011), Silva-Villa and Larsen (2011), da Silva et al. (2012), Eldridge (2012), among others. There are currently some public Monte Carlo synthesis codes for further research in the area, such as the SLUG package (https://sites.google.com/site/runslug/) (da Silva et al. 2012) and the MASSCLEAN packages (http://www.physics.uc.edu/~bogdan/massclean.html) (Popescu and Hanson 2009, 2010a, b).

A natural effect of Monte Carlo modelling is direct visualization of the range of scatter in model results. However, the relevant results in Monte Carlo sets are the distribution of results instead of their range (I discuss this point later). Whatever the case, these phenomenological studies have opened up several questions on the modelling of stellar populations and their applications. Some of these questions are as follows. (a) What are the limitations of traditional synthesis models, especially for low values of (among others Cerviño and Valls-Gabaud 2003, Cerviño and Luridiana 2004, Silva-Villa and Larsen 2011)? (b) What is actually computed by traditional synthesis models, how are they linked to Monte Carlo modelling, and are they the limit for → ∞ (e.g. use of terms such as discrete population synthesis vs. continuous population synthesis by Fouesneau and Lançon 2010, or discrete IMF vs. continuous IMF models by Piskunov et al. 2011) ? (c) How can Monte Carlo modelling be used to make inferences about stellar systems (Fouesneau et al. 2012, Popescu et al. 2012)? In this study I aim to solve some of these questions and provide additional uses of stellar population modelling. I begin with the modelling itself.

¹ Monochromatic N_eff values for old stellar populations can be found at http://www.bo.astro.it/~eps/home.html and http://www.iaa.es/~rosa/research/synthesis/HRES/ESPS-HRES.html (González Delgado et al. 2005) for young and intermediate SSPs. Back.