


The theory of forming dusty galaxies at high-redshift has been a confounding, frustrating, and difficult subject under the general umbrella topic of astrophysical galaxy formation. As we will present in this section, while theorists have thrown every tool in their toolbox at the problem, and the methods that aim to model the origin and evolution of high-z starbursts are extremely diverse, nearly all models struggle with (generally different) aspects of matching observations of high-z dusty galaxies.
By and large, as with observations, the principle focus of theorists modeling DSFGs has been in modeling the high-z Submillimeter Galaxy population. This said, surveys of other dusty galaxy populations with Spitzer and Herschel have motivated some targeted modeling efforts (e.g. Lacey et al., 2008, 2010, Narayanan et al., 2010a, Niemi et al., 2012), and have at the least provided a strong constraint on general galaxy formation models (e.g. Somerville et al., 2012).
Our principle aims in this section are to overview the general methods employed in modeling high-z dusty galaxies, and to describe the main differences in them, along with some of their strengths and weaknesses. We will then summarize the major results in the theoretical literature of dusty galaxy formation over the last decade, and conclude the section with an outline of key differences and observable tests of the models. Finally, we note that this section is a review solely of the formation of dusty galaxies. For a more comprehensive recent review of galaxy formation theory, please see Benson (2010).
10.1. Overview of Dusty Galaxy Modeling Methods
In this section, we will first overview the principle methods that have been used in modeling high-z dusty systems, paying particular attention to how they model the details of the FIR/submm emission. The modeling methods fall into three broad classes: Semi-Analytic Models (SAMs), Cosmological Hydrodynamic Simulations, and Hybrid Models. We will briefly discuss Empirical (also known as “Backwards Evolution”) methods in the models section as they are often described as “models” and compared to observations. This said, as we will point out in this section, while empirical methods are useful in predicting the evolution of observed source counts, they are not bona fide models. Rather, they are purely based on extrapolation of observations, and thus not predictive theories of galaxy formation. Hence, our discussion of these types of methods in this review will be limited. We summarize the salient points of galaxy formation modeling methods in Table 4, as they pertain to DSFG modeling.
The main purpose in this section is to highlight both the complementarity between methods, as well as the basic level at which astrophysical processes are no longer directly simulated, but rather implemented in the simulations via an analytic prescription. In principle, every simulation requires an analytic prescription at some level. The difference in scale where these prescriptions are imposed vary dramatically for galaxy formation models that aim to simulate dusty galaxies, and can range from prescriptions on the parsec scale, to prescriptions on dark matter halo-scales. In Table 5, we summarize the main points made in this section, and in particular, outline key testable predictions made by many of the major SMG modeling groups.
The term “Semi-Analytic Modeling” (SAMs) typically refers to modeling methods that draw on a combination of both numerical simulations (to model the cosmic evolution of dark matter halos), and analytic approximations (to model the structure of galaxies, and physics associated with the baryonic/luminous component of galaxies). The original framework itself goes back to seminal papers by White & Frenk (1991), Cole (1991) and Lacey & Silk (1991), and was advanced substantially by a number of groups (Baugh et al., 1996, 1998, Kauffmann et al., 1993, Kauffmann, 1996, Kauffmann & Charlot, 1998, Kauffmann et al., 1999, Somerville & Primack, 1999). Because SAMs are typically a combination of large-scale dark matter only simulations 24 with fairly detailed analytic prescriptions of galaxy formation and evolution, particular SAMs that drive a large number of papers are typically referred to in the literature by their host institution/city, such as the “Durham SAM”, the “Santa Cruz SAM”, or the “Munich SAM”. One exciting aspect of SAMs is that they are relatively inexpensive to run. Because of this, it can be quite inexpensive to run a large range of model parameter choices (and variations on prescriptions for physical processes) with the SAM methodology (e.g. the new publicly available code, Galacticus Benson, 2012). Because of this, SAMs are readily used for isolating the effects of an individual astrophysical process (see Croton et al., 2006). One promising way forward with SAMs is the construction of large grids of models that aim to constrain galaxy formation parameter spaces via comparison to observations through Markov Chain Monte Carlo models (e.g. Lu et al., 2011, 2012).
For the majority of SAMs, the only directly simulated quantity is the dark matter-only structure formation models. With the assumption of a given cosmology and initial perturbation spectrum, these simulations are evolved forward to capture the gravitational collapse of dark matter halos, and their mergers with cosmic time. The analytic prescriptions by which the baryonic physics is treated is usually what sets the principle distinction between different SAMs. A small number of SAMs include additional layers of simulated quantities (e.g. Lagos et al., 2013), though to our knowledge no SAM numerically solves the Euler equations, and typically treat the geometries of galaxies as highly simplified. In Table 2 of his review article, Benson (2010) summarizes some of the key physical processes that are (or are not) captured by five major semi-analytic codes, though the detailed treatment of an individual physical process (e.g. star formation) can vary from model to model, and even individual models (e.g. the Durham Model) can have a number of sub-branches that differ in detail. Generally, the analytic prescriptions for baryonic physics that are incorporated into SAMs include gas cooling, feedback from stellar evolution and AGN, star formation in molecular gas, and chemical enrichment of the ISM and IGM. The structure of galaxies is necessarily derived via simplified prescriptions (e.g. exponential disks; disks with some bulge component; ellipticals).
The models of galaxies are related to observations in a semi-analytic framework typically via one of two methodologies. The first is to directly apply dust radiative transfer simulations to the galaxy model outputs. A grid of dust distribution and stellar sources is set up in a simplified geometry (e.g. an axisymmetric disk with a bulge component) corresponding to the assumption of the source structure in the SAM. The emission is then calculated from this analytic geometry self-consistently with a code such as grasil (e.g. Silva et al., 1998). Because the source geometry is analytically defined, it is nontrivial to describe the resolution of a SAM, other than the typical force resolution of the base dark matter-only simulation. The model galaxies are typically broken up into some number of grid elements for the grasil calculations, though within that, sub-resolution molecular clouds are included making the definition of 'resolution' even more complicated to define in the SAM framework. A key advantage of this formalism is that the computation time is relatively quick, allowing for parameter-space surveys in (e.g.) the assumed IMF or dust content. This methodology has been employed by (as an example) Baugh et al. (2005), Lacey et al. (2008), González et al. (2011) and Fontanot & Somerville (2011).
The other common means for prescribing the SEDs to galaxies assigned to halos in SAMs is via SED templates derived for observed galaxies (e.g. Dale & Helou, 2002, Chary & Elbaz, 2001, Rieke et al., 2009). These templates, calibrated for z ~ 0 LIRGs and ULIRGs, can usually be parameterized in terms of the bolometric luminosity of the galaxy, which is a readily available quantity from SAMs. Because these methods are rooted in observations, the SEDs are not predictive. This method is advantageous in that it is even faster than the aforementioned coupling of simplified geometries with dust radiative transfer codes, is not dependent on the particular geometry assumed for a given galaxy, not dependent on the resolution of a gridded model, and is grounded in observational data. The uncertainty, of course, is whether locally-calibrated observational templates are applicable to galaxies at the same luminosity at high-z. A recent example of this sort of application of observed SED templates to SAMs is presented in Somerville et al. (2012), Kim et al. (2014).
10.1.2. Cosmological Hydrodynamic Simulations
Cosmological hydrodynamic simulations build on the dark matter structure formation models that are the base of SAMs, and hydrodynamically simulate the evolution of the baryonic components of galaxies. This is the major difference between SAMs and cosmological hydrodynamic simulations: the former assign the physical properties of galaxies via analytic models, while the latter derive them from bona fide hydrodynamic simulations. Each has distinct advantages, and the methods are complementary. SAMs provide the only feasible possibility for surveying parameter spaces, and describing a reasonable landscape within which to pursue more costly simulations. Hydrodynamic simulations offer the advantage of potentially providing a more realistic model for the formation and evolution of galaxies, but are so costly that they typically can only explore a few parameter choices. When a set of simulations do not match an aspect of observations (as they are bound to do), it can be very difficult in cosmological hydrodynamic simulations to identify the source of the mismatch.
A number of publicly available codes exist for the purposes of cosmological simulations that are commonly employed 25, such as amiga, gadget, enzo, flash, and ramses (Knebe et al., 2001, Springel, 2005, The Enzo Collaboration et al., 2013, Fryxell et al., 2000, Teyssier, 2002), as well as other well-known and tested codes that are not necessarily public (e.g. gasoline, art and arepo; Wadsley et al., 2004, Kravtsov, 1999, Springel, 2010)) 26 The physics included in hydrodynamic cosmological simulations is varied even among a common set of codes, and is certainly extremely diverse when considering simulations run with different codes. The hydrodynamic methods employed vary from code to code as well, ranging from particle based methods (i.e. smoothed particle hydrodynamics; SPH), to grid-based codes (most principally adaptive mesh refinement; AMR), to hybrid-based methods. In many ways, the different methods agree between one another, though in others there can be stark differences (see, e.g., Nelson et al., 2013). A number of code comparison projects have been performed, and are currently underway (e.g. Scannapieco et al., 2012, Kim et al., 2014).
10.1.3. Idealized and Hybrid Models
As a complementary method to cosmological hydrodynamic simulations, a number of groups have explored the formation of dusty galaxies via idealized hydrodynamic galaxy simulations. These typically involve evolving forward the hydrodynamic properties of baryons in galaxies that have been initialized with idealized conditions. These are generally disk galaxies, or mergers between two disks. These have an advantage of allowing for relatively high resolution (a few - 100 pc). The disadvantage, of course, is that there is no knowledge of the cosmological context of the galaxies. So, perturbations in the galaxy structure due to environment are lost, as well as the ability to simulate surveys of galaxies.
These simulations are typically coupled with dust radiative transfer to calculate their observed SED properties. This is their main advantage when comparing to SAMs or cosmological hydrodynamic techniques. Idealized simulations offer high enough resolution that the distribution of luminous sources and dust are well-known for the calculation of the emergent SED. Similarly, idealized simulations typically offer high temporal resolution, which allows for studies in the color evolution of galaxies.
In order to infer cosmological statistics from idealized simulations, a number of groups (e.g. Hopkins et al., 2010, Hayward et al., 2013b) have developed techniques where they combine duty cycles of particular events with galaxy merger rates and mass functions derived from cosmological dark matter-only simulations. As an illustrative example, Hayward et al. (2013b) inferred the number counts of 850 µm-selected SMGs by running a large suite of idealized disk galaxies and mergers over a large range of galaxy masses and merger mass ratios through dust radiative transfer calculations. This generated the typical submm duty cycle as a function of galaxy mass and merger mass ratio. These authors then combined these duty cycles with observed stellar mass functions from z ~ 2-4 (in order to derive the contribution to the submm number counts from non-interacting galaxies), as well as theoretical galaxy-galaxy merger rates derived from cosmological simulations (in order to add in the contribution from galaxy mergers). This technique has the advantage of effectively keeping ~ 1 - 100 pc resolution over large volumes (e.g. Hopkins et al., 2013c, a, d), which is entirely unfeasible with a bona fide cosmological simulation. The downside is that the impact of events such as gas accretion from the intergalactic medium, or galaxy harassment in dense environments may not be captured in this technique (though see Moster et al., 2014).
These sorts of hybrid models are unlike cosmological simulations or SAMs in that they cannot be evolved forward to infer the properties of the descendents of high-z DSFGs. However, as we will discuss, there are a large number of observations that can constrain the models. These range from the mean physical properties of the galaxies of interest (e.g. SFRs, gas fractions, stellar masses and halo masses) to statistical inferences such as the breakdown of galaxy morphologies, and overlap with other galaxy populations.
A number of empirical methods exist in the literature to predict the evolution of number counts at different wavelengths. These methods are not 'models' as the SAMs, cosmological simulations, or hybrid methods discussed previously in that they provide no physical information about the observed galaxies, and almost solely utilize observed parametric forms for luminosity functions and galaxy SEDs in order to make their predictions. In other words, rather than being ab initio models of galaxy formation and evolution, the empirical methods are phenomenological models with little to no physics that are constrained to fit the existing observations when making predictions for future surveys. This said, they provide strong constraints both on the SED shapes and potential evolution of galaxy luminosity functions, and are well-used in the literature as a consequence.
While the details are varied, the basic principles underlying empirical methods are similar. At their heart, empirical methods rely on combining observed SED templates of galaxies with observed luminosity functions. The free parameters in the luminosity function are then tuned such that the model matches the known number counts of existing populations in order to make predictions for surveys at as yet unobserved wavelengths and/or redshifts. This is, of course, a simplistic description of empirical methods, and indeed many groups have added significant complexities to this basic idea. For example, Negrello et al. (2007) combined phenomenological models of starburst galaxy SED evolution with the Granato et al. (2004) SAM in order to make specific predictions regarding the counts of SMGs when considering lensed populations.
10.2. Main Results from Theories of Dusty Galaxies
As alluded to in § 10.1, forming dusty galaxies at high-z has been a confounding problem for theorists across the board. In this section, we summarize the main results over the past decade, divided by the general class of methods that have attempted to understand luminous sources at high-z. As the reader will notice, coming up with galaxies in simulations that can reproduce some observed and inferred physical attributes of high-z dusty galaxies is fairly straight forward. Doing so while also matching constraints from other low or high-z galaxy populations simultaneously is significantly harder. To our knowledge, no model to date has simultaneously matched the observed number counts of SMGs while also matching their inferred physical properties, as well as the z ~ 0 stellar mass function in an ab initio manner. A comparison of some of the outlined methods may also be found in van Kampen et al. (2005). As a reference for the forthcoming section, in Figure 49, we show the observed 850 µm differential number counts with a variety of theoretical models overlaid.
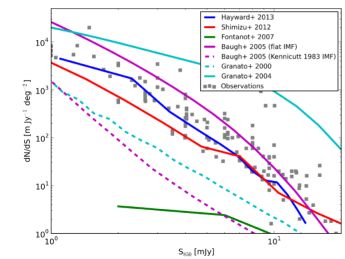 |
Figure 49. Observed 850 µm differential number counts (grey squares), with theoretical curves from various models over-plotted as colored lines (Granato et al., 2000, 2004, Baugh et al., 2005, Fontanot et al., 2007, Shimizu et al., 2012, Hayward et al., 2013b). We only include the typical flux density range of observed points that are considered by theoretical models that aim to match the SMG number counts. Note, we do not include the Davé et al. (2010) hydrodynamic model, or empirical models, as the theoretical counts in these cases are forced to match the observed counts by construction. |
A number of SAMs are contemporaneous with the first submm/IR surveys at high-z, and are summarized in full in the last major review on SMGs by Blain et al. (2002). Of note, Guiderdoni et al. (1998), Blain et al. (1999), and Devriendt & Guiderdoni (2000) provided predictions for and comparisons with these nascent deep submm surveys. These, and other predictions at the time tended to under-predict the number of SMGs, a problem that, as we will see, will prove to be pervasive in SAMs. In particular, these papers provided early indications that extreme assumptions were necessary to produce SMGs.
Once deep submillimeter number counts were maturing in the literature, the difficulty in producing enough SMGs in cosmological models was pointed out in a seminal paper by Baugh et al. (2005). These authors updated the then-current version of the Durham galform SAM (Cole et al., 2000, Granato et al., 2000) to investigate the physical properties of high-z SMGs. By coupling their model with grasil dust radiative transfer calculations, Baugh et al. (2005) found that they under-predicted the observed number counts of SMGs by a factor of ~ 30 - 50. Constraining the model was a goal of simultaneously matching the observed LBG distribution at high-z, as well as the z = 0 K-band luminosity function and IRAS 60 µm luminosity function. Beyond this, the model had a goal of not allowing the dust temperature to be a free parameter, which was a key update to empirical models that pre-dated this one.
As a solution to matching the observed SMG number counts while retaining a match to the observed LBG and z = 0 K-band luminosity function, Baugh et al. (2005) modified three major aspects of the original Granato et al. (2000) model. First, the star formation time scale in disks is modified to be dependent on the circular velocity, rather than the dynamical time scale. This has the effect of making galaxies more gas rich. The second modification was to allow starbursts in galaxy mergers that involved minor mergers (down to mass ratios of 1:20), rather than just in major mergers, if the minor mergers were sufficiently gas rich (fgas > 0.75). The third modification, which is likely the most dramatic change, was to the stellar initial mass function in starburst galaxies. For quiescently star-forming galaxies, the model imposed a Kennicutt (1983) model IMF, with dn / d ln(m) ∝ m-x, with x = 0.4 for M < 1 M⊙ , and x = 1.5 for M > 1 M⊙ . For starbursts that are triggered by galaxy mergers, the IMF was modified to being extremely top heavy (in fact, flat), with x = 0 for all stellar masses. While the transition from a Kennicutt (1983) IMF to a flat IMF does not have a physical basis, there are a few attractive aspects to a top-heavy IMF in starbursts (beyond those already outlined in § 5.4). First, the majority of stars formed in galaxy mergers are done during early quiescent phases, rather than bursts (e.g. Cox et al., 2008). Hence, modifying the IMF in bursts alone does not severely impact the present-epoch stellar mass function. Second, increasing the fraction of massive stars formed in a generation results in both more UV luminosity per stellar mass formed, as well as more dust. Hence, while the bolometric luminosity of the galaxy increases, the spectrum is allowed to remain cold, fostering the formation of submillimeter-detectable galaxies. In this model > 99% of SMGs are triggered by galaxy mergers, and hence the IMF is predicted to be flat in essentially all SMGs. The difference in the Baugh et al. (2005) predictions for a Kennicutt (1983) and flat IMF is shown in Figure 49.
These models were examined further by González et al. (2011), who examined the physical properties of the SMGs formed in the Baugh et al. model in detail. González et al. (2011) find that ~ 75% of the SMGs formed in the Durham model do so in minor (mass ratio > 1:20) mergers, with baryonic gas fractions > 75%. Roughly 22 % of the SMGs are formed in major mergers, and 0.7% in quiescent galaxies. This is in stark contrast to some of the results from cosmological hydrodynamic and hybrid models, as we will discuss later. The resulting morphology of these galaxies is a disk plus bulge, with most (> 2/3) of the descendants having a bulge to total (B / T) mass ratio > 0.5.
Swinbank et al. (2008) showed that the Baugh et al. (2005) model for SMG formation matched the observed SMG number counts, FIR and mm-wave colors, and potentially redshift distribution (though this is, of course, an area of hot debate; c.f. § 4). Similarly, a number of works have expanded this model to investigate other galaxy populations and shown reasonable correspondence with observations. Le Delliou et al. (2005, 2006) examine the properties of Lyα emitters in the Baugh et al. (2005) galform model, and find good correspondence with the observed counts, magnitudes and equivalent widths (modulo assumptions regarding a fixed escape fraction). Similarly, Lacey et al. (2008) compared the galaxies formed in the Baugh et al. (2005) model to existing Spitzer data to show that the model matches a number of IR constraints, including the strong evolution in the galaxy mid-IR luminosity function. In particular, these authors find that the modified IMF (i.e. flat IMF in starbursts) is necessary to match the observed mid-IR luminosity function evolution, and that a normal IMF in starbursts may be excluded as it predicts too little evolution in the Durham SAM.
However, Swinbank et al. (2008) show that the the synthetic K-band and mid-IR (3 - 8 µm) colors of the model galaxies in the Baugh et al. (2005) model are too low by up to a factor ~ 10 as compared to observed SMGs. This owes to a typical stellar mass of ~ 1010 M⊙ for SMGs in the Durham model. Qualitatively, this can be explained by the idea that a flat IMF (in merger-driven starbursts) was necessary to reproduce the observed cold dust colors of SMGs in the model. The IMF is only flat in merger-driven bursts in this model, though there are not enough mergers between massive galaxies to account for the full SMG number counts. Hence, the model required lower mass galaxies to serve as SMGs, which shows tension with observed K-band and mid-IR colors. In a similar vein, Bothwell et al. (2013a) showed that at z > 3, observed SMGs and those made in the galform model are discrepant in their predicted and observed molecular gas fractions by a factor of 2, with the model gas fractions approaching unity by z ~ 4. While gas fractions in SMGs are observed to be high (modulo potential X-factor effects; c.f. § 8.6), a gas fraction (fgas = Mgas / (Mgas + M*) > 0.9 as predicted by the galform model for z ~ 4 galaxies is not currently supported by observations. Finally, the flat IMF that galform requires in order to match the observed SMG number counts and evolution in the galaxy mid-IR luminosity function has not been observed in any nearby environment (see the recent review by Bastian et al., 2010). While some circumstantial evidence may point toward more bottom-light IMFs in heavily star-forming environments (c.f. § 5.4), nothing approaching an IMF as extreme as a flat one has ever been observed. Beyond this, joint constraints on the X-factor, stellar mass, dynamical mass and IMF of observed high-z SMGs exclude a flat IMF, in the case where the gas reservoir's size is relatively compact at low-J (Tacconi et al., 2008). In summary, the flat IMF galform model put forth by the Durham group has shown success in matching a number of observations of high-z galaxies. On the other hand, there are a few notable mismatches when confronted with observations that suggest that the galform model, at least as far as dusty galaxies at high-z go, will lead to further physical insight as it is further tuned in an effort to fully match basic observational constraints of SMGs.
In complementary work, Fontanot et al. (2007) used the Model for the Rise of Galaxies and Active Galactic Nuclei (morgana) to investigate whether the observed 850 µm counts could be accounted for in hierarchical galaxy formation SAMs without any extreme assumptions regarding the IMF. Similar to Baugh et al. (2005), Fontanot et al. (2007) combined their SAM with grasil radiative transfer in order to predict the synthetic colors of their model galaxies. Utilizing a Salpeter IMF, and an updated model for gas cooling onto halos, this group was able to match the observed 850 µm number counts. The physical form of the SMGs formed in the morgana simulations are notably different from those formed in galform, however. While the latter suggested that SMGs were almost exclusively mergers, Fontanot et al. (2007) found that mergers only dominated galaxies with the highest star formation rates, SFR > 200 M⊙ yr-1. As we will discuss, the idea of SMGs owing to both heavily star-forming (non-merging) galaxies, as well as mergers will be prevalent in both the cosmological hydrodynamic simulations, as well as the hybrid models for SMG formation. In principle, the difference in the models is that the Fontanot et al. (2007) model is able to form heavily star-forming galaxies without mergers owing to more efficient gas cooling from the IGM. It is noted, however, that this model over produces stars in massive galaxies, and therefore is incompatible with observations of local galaxies.
Somerville et al. (2012) presented an updated form of the Somerville & Primack (1999) SAM (i.e. the “Santa Cruz SAM”) that was combined with estimates for dust attenuation by both diffuse dust and stellar birth clouds surrounding young clusters. The energy absorbed by dust was assumed to be re-radiated in the infrared, and combined these with both theoretical SED templates by Devriendt et al. (1999), as well as the locally-calibrated observed SED templates by Rieke et al. (2009). These authors found that in order to reproduce the (rest) UV and optical luminosity functions at high-z, an evolving dust-to-metals ratio was necessary. In other words, galaxies at a comparable luminosity at high-redshift compared to a local analog needed less dust obscuration. This made reproducing the observed properties of dusty galaxies at high-z more difficult, however, and as a consequence the Somerville et al. (2012) model was unable to match the observed 250 µm SPIRE number counts, as well as the 850 µm Scuba counts. As shown by Niemi et al. (2012), the Somerville et al. (2012) model works rather well at lower redshifts (i.e. z < 2), though shows increasing tension with observations at z > 2. The discrepancy in the Santa Cruz SAM in matching IR and submm counts becomes progressively worse at increasing wavelength. Interestingly, these models show good agreement between the physical properties of their identified Herschel-detected galaxies, and those inferred from observations (including stellar and gas masses, star formation rate, and disk sizes). The Somerville et al. (2012) and Niemi et al. (2012) models predicted that galaxies of increasing infrared luminosity were more likely to owe their origin to mergers, though only roughly half of Herschel-detected galaxies were formed in mergers: the other 50% arose from heavily star-forming galaxies fueled by the gas-rich environment characteristic of the z ~ 2-4 Universe.
10.2.2. Cosmological Hydrodynamic Simulations
One of the first cosmological hydrodynamic simulations to address the origin of high-z SMGs were by Fardal et al. (2001) 27 utilizing the parallel SPH code, TreeSPH. This work combined cosmological SPH galaxy formation models with 7 h-1 kpc spatial resolution (equivalent Plummer softening length) with an empirical recipe for converting the SFR of a galaxy to 850 µm flux density (assuming a dust temperature and SED slope β) to calculate the synthetic emission properties of high-z galaxies. These authors were amongst the first to advocate a scenario in which nearly all SMGs at high-z formed from massive, heavily star-forming galaxies that are not undergoing a merger. This will be a common feature of cosmological hydrodynamic models. A key feature of this model is that SMGs are typically not undergoing starbursts, but rather typically have much lower SFRs than observations suggest of the population, with a median simulated SFR of ~ 100 M⊙ yr-1 with long duration SFR timescales.
Finlator et al. (2006) discussed a similar scenario for the formation of SMGs. When exploring the physical properties of z ~ 4 galaxies in a cosmological hydrodynamic simulation run with gadget, these authors noted a number of galaxies in their simulated volume with SFRs exceeding 100 M⊙yr-1, with two exceeding 1000 M⊙ yr-1. Subsequently, Dekel et al. (2009a) showed that these large SFRs could owe to the growth of galaxies via the accretion of cold gas from the IGM, at a time when the Universe was denser, and hence cooling times were shorter. Dekel et al. (2009a) suggest that approximately half of SMGs with flux densities S850 > 5 mJy form in mergers with mass ratio 28 > M1 / M2 > 0.1, while the other half owe their large SFRs to smoother gas accretion from the IGM.
Building on these studies, Davé et al. (2010) performed the most extensive study of the physical properties of SMGs in cosmological hydrodynamic simulations to date. These authors ran a 100 Mpc h-1 cosmological simulation with the N-body/SPH code gadget, with an effective resolution of 3.75 kpc h-1. The simulations, which included physical prescriptions for momentum-driven winds and chemical enrichment, have previously shown good agreement with the galaxy mass-metallicity relation (Finlator & Davé, 2008), observed IGM enrichment (Oppenheimer & Davé, 2006, 2008, 2009), and the cosmological evolution of the UV-luminosity function. Davé et al. (2010) identified SMGs as the most heavily star-forming galaxies in their simulations, and chose all SMGs above a given SFR threshold such that their abundance matched the observed number counts of SMGs. Hence, these simulations took the ansatz of matching the number counts by construction, and asked what the physical properties of these galaxies in cosmological hydrodynamic simulations were. This threshold SFR for SMG identification was 180 M⊙ yr-1.
As in previous cosmological hydrodynamic simulations, the bulk of the SMGs modeled by Davé et al. (2010) were massive star-forming galaxies that were not undergoing a merger-driven starburst. As such, these galaxies, for the most part, live on an extension of the galaxy SFR-M* main sequence defined by lower-mass galaxies. The model galaxies had typical log (M*) = [11,11.8], baryonic gas fractions ~ 20 - 40%, and SFRs ranging from 180 - 570 M⊙ yr-1. While the many of the physical properties of the simulated SMGs in the Davé et al. (2010) model match those inferred from observations, the SFRs tend to be a factor ~ 2 - 5 lower than what is observed. This dilemma originates in the fact that there are not enough mergers in the simulations for all SMGs to be accounted for by mergers, at least for galaxies as massive as M* ~ 1011 M⊙ (e.g. Guo & White, 2008, Hopkins et al., 2010). Without bursts, the SFR is, to first order, regulated by the gas accretion rate from the IGM, which is dictated by the ever-growing gravitational potential in the halo (e.g. Dekel et al., 2009b). Similar issues plague most cosmological simulations, which fail to match the observed normalization of the SFR-M* relation at z ~ 2 (e.g. Davé, 2008, Weinmann et al., 2011). Suggestions of a bottom-light IMF have been put forth to ameliorate the issue (e.g. Narayanan & Davé, 2012, 2013), though this may come at the cost of introducing a tension with stellar absorption line measurements in local massive galaxies, the presumed descendants of high-z starbursts (c.f. § 5.4). In the Davé et al. (2010) model, 1 galaxy out of the 41 in their simulated sample was undergoing a major (M1 / M2 > 1/3) merger.
Finally, Shimizu et al. (2012) performed cosmological hydrodynamic s imulations with gadget as well, though including a simplified dust absorption model and grey-body emission for the SED. These authors find that they are able to reproduce the number counts and clustering amplitude of observed SMGs, and predict a stellar mass of > 1011 M⊙ for all S850 > 1 mJy SMGs (note that this is different from the canonical definition used by the other theoretical models described here, of S850 > 5 mJy). Shimizu et al. (2012) find many more galaxies with SFR > 500 M⊙ yr-1 than Davé et al. (2010), though also simulate many more galaxies such that it is not clear how the percentages compare. The stellar masses found in this study are amongst the largest compared to the other models discussed thus far, with log(M*) = [11,12.4].
10.2.3. Idealized and Hybrid Simulations
High-resolution galaxy merger and isolated disk simulations have long been examined to study the detailed star formation properties of star-forming galaxies. Chakrabarti et al. (2008) coupled a series of eight 1:1 idealized major merger gadget SPH simulations with radishe, a 3D Monte Carlo radiative equilibrium dust radiative transfer code to calculate the synthetic SED properties of these galaxies. Chakrabarti et al. (2008) showed, as has been previously seen by a number of groups, that galaxies of increasing mass have increasing star formation rates, and that coplanar galaxy mergers tend to undergo larger bursts than those merging orthogonally. These authors examined the time evolution of the 850 µm flux density for galaxy mergers, as well as the black hole growth rates, and synthetic Spitzer and Herschel colors.
The models of Chakrabarti et al. (2008) found peak SFRs of 3000-4000 M⊙ yr-1, comparable to some inferred estimates of observed galaxies. This said, they were only marginally able to produce a galaxy that was as bright as S850 ≈ 4 mJy for a timescale of 10-20 Myr with even their most massive galaxies. The brightest galaxy in this study (4 mJy at 850 µm) had a stellar mass M* = 9.4 × 1011 M⊙ , suggesting that the majority of S850 > 5 mJy SMGs in this model would require M* > 1012 M⊙ . Referring to § 5.3, this includes only the most massive galaxies utilizing the Michalowski et al. (2012) estimates, which are at the upper end of SMG mass estimates and potentially not even valid since they exceed constraints from dynamical mass estimates.
Narayanan et al. (2010c) examined the properties of a series of galaxy mergers over a range of galaxy masses and merger mass ratios, as well as idealized isolated disk galaxies utilizing gadget as the N-body/hydrodynamics solver. These authors coupled these simulations with sunrise, a 3D Monte Carlo dust radiative transfer code in order to produce the simulated SED and nebular line properties of their simulated galaxies (Jonsson, 2006, Jonsson et al., 2010, Jonsson & Primack, 2010). A key difference between sunrise and radishe is the inclusion of photodissociation region (PDR) modeling. The UV absorption and subsequent long-wavelength re-emission from the cold PDRs surrounding young stellar clusters formed in the galaxy merger is captured in sunrise via the inclusion of mappings photoionzation calculations (Groves et al., 2008). Narayanan et al. (2010c) suggested that the bulk of the 850 µm flux density to arise during a galaxy merger was due to the obscuration by stellar birth clouds, though neglecting these, but treating the molecular ISM as having a volume filling fraction of unity could achieve the same effect. These galaxies produced SMGs with a range of peak flux densities, from the common S850 = 5 mJy to the extreme 15 mJy (comparable to, e.g. GN20). The stellar masses ranged from ~ 3 - 8 × 1011 M⊙ , and the galaxies lived in haloes ranging from ~ 7 - 20 × 1012 M⊙ .
Follow-up work by Narayanan et al. (2009) investigated the simulated CO properties of the Narayanan et al. (2010c) model SMG sample by combining the gadget simulations with turtlebeach (Narayanan et al., 2006a, b, 2008b, d) 3D non-LTE Monte Carlo molecular line radiative transfer calculations in post-processing. These authors found that SMGs that formed in galaxy mergers show broad CO line widths, varied CO morphologies, and typically subthermal CO excitation, comparable to previous observations (c.f. § 8.5).
Similarly, Narayanan et al. (2010b) examined the synthetic optical and Spitzer colors from these simulations with a goal of understanding the physical properties of DOGs. In this model, DOGs may owe to a variety of origins, with lower-luminosity DOGs generally being ascribed to isolated disk galaxies, and higher luminosity DOGs arising almost exclusively from mergers. The most luminous DOGs with a power-law mid-IR SED may represent an transition stage between a starburst-dominated merger-driven SMG, and an optical quasar phase. During this phase, the black holes grow rapidly, and rise from lying below the MBH - σ relation to on it. Moreover, because of the diversity of the DOG population, there is a large overlap between the SMG and DOG populations in this picture, a result that is confirmed by at least some observations (Pope et al., 2008a).
The Narayanan et al. (2009, 2010c) series of models were expanded upon substantially in a series of papers by Hayward et al. (2011, 2012, 2013a, 2013b) and Hayward (2013). In summary, these papers comprise a nuanced picture of SMGs in which SMGs do not owe specifically to either isolated disk galaxies, or galaxy mergers, but a combination of the two. Along with these, blended pairs of galaxies (sometimes physically associated, other times, not) make up the observed SMG number counts.
Hayward et al. (2011) showed that during the coalescence of a galaxy merger, galaxies become more compact, and drop in dust mass driving an increased dust temperature. This has the effect of starbursts being relatively inefficient at boosting submm flux density. These authors showed that the relationship between the SFR of a galaxy and 850 flux density is relatively weak. A major finding from this work, as well as Hayward et al. (2012), was that it is unlikely that starbursts alone can make up the full SMG galaxy number counts, and that pairs of galaxies in-spiralling in toward a final merger coalescence may contribute substantially.
| Model Type | Directly Simulated † | Scale of Analytic Approximations | How Radiative Transfer is Done |
| SAM | Cosmic Dark Matter | Galaxy Scales | Axisymmetric analytic galaxy |
| models coupled with 3D dust | |||
| radiative transfer | |||
| Cosmological | Cosmic Dark Matter | ≲ 5 kpc | Either N/A or |
| Hydro | Baryons in Galaxies and IGM | analytic approximations | |
| Idealized | Baryons in Galaxies | Molecular Cloud (≲ 100 pc) | 3D dust radiative transfer |
| (decoupled from environment) | |||
| Hybrid | Cosmic Dark Matter | Molecular Cloud (≲ 100 pc) | 3D dust radiative transfer |
| Baryons in Galaxies | |||
| (decoupled from environment) | |||
| † This column refers to what component of the galaxy formation models is directly simulated via numerical modeling (as opposed to via analytic approximation) | |||
While idealized simulations such as those performed by Chakrabarti et al. (2008) and Narayanan et al. (2009, 2010a, c) have the advantage of having high-enough spatial resolution that their physical geometry, and consequent radiative transfer solutions are well-characterized, they offer no information about the general population as they are not cosmological calculations. The hybrid methodology to extrapolate the properties of idealized simulations to a cosmological context was first developed by Hopkins et al. (2010). The basic construct behind these models was to utilize theoretical halo mass functions, and assign galaxies to them utilizing an abundance matching technique (e.g. Conroy & Wechsler, 2009, Behroozi et al., 2010). These would then be combined with the results of high-resolution merger calculations in order to determine the typical burst luminosity from a galaxy merger, or steady-state SFR from an isolated disk galaxy of a given mass. By convolving the two, Hopkins et al. (2010) measured the contribution of mergers, AGN and isolated-disk galaxies to observed infrared luminosity functions.
This methodology was improved upon by Hayward et al. (2013b), and directly applied to observations of high-z dusty galaxies. By running a large suite of idealized disk galaxy simulations, as well as galaxy mergers over a range of galaxy masses, merger mass ratios, and merger orbits, these authors derived a mean submm duty cycle for galaxies as a function of these galaxy physical properties. In order to simulate the results from deep submm surveys, Hayward et al. (2013b) then combined these results with simulated galaxy merger rates, as well as observed stellar mass functions (in order to quantify the abundance of non-interacting galaxies). By combining this multi-scale methodology, these authors found they were able to match the observed SMG number counts when accounting for the full contribution of merger-induced starbursts, non-interacting galaxies, and galaxy pairs that were physically associated. Hayward et al. (2013a) showed that physically unassociated galaxies (i.e. galaxies at substantially different redshifts) may also contribute to the observed SMG number counts.
These sorts of hybrid methods have both distinct advantages and disadvantages. The most positive aspect of this multi-scale methodology is that it it allows for an extremely large dynamic range of physical processes to be modeled. For example, the Hayward et al. (2013b) model effectively has ~ 50 - 100 pc resolution (i.e. resolving the surfaces of large giant molecular clouds) over cosmological volumes. This sort of treatment is important when modeling both the detailed processes that occur in a chaotic system, such as a galaxy merger, as well as resolving the spatial distribution of luminous sources and dust. Because the simulations are anchored in high-resolution hydrodynamic models, few assumptions regarding the spatial geometry of the system have to be made going into the radiative transfer calculations. This is something that cosmological simulations, at least in their current state, are unable to do given resolution limitations. On the down side, this approach is not truly ab initio as a bona fide cosmological simulation. For example, the hybrid approach does not allow for a direct investigation as to the role of continuous gas-replenishment of galaxies from the IGM.
10.3. Testable Predictions and Key Differences between Models
In Table 5, we summarize the key testable predictions of some of the major models for SMG formation in the literature. We provide literature references for each model, as well as list the major codes and methodologies used. While the exact same physical quantities are not always available for each model, Table 5 should provide a relatively direct way of comparing the direct predictions from different SMG formation models. While some of the predictions were available from the literature, others had to be obtained via private communication. Oftentimes, the simulations were no longer available owing to computer crashes and retirements; hence, some predictions may not be available.
| Model Reference | Code | Methodology | Distinguishing Predictions for z = 2 SMGs |
| Granato et al. (2004) | galform | SAM | No Predictions Available |
| Baugh et al. (2005) | galform | SAM | M* = 2.1 × 1010 ‡ M⊙ |
| González et al. (2011) | grasil | Dust Radiative Transfer | Mhalo = 2.2 × 1012 ‡ M⊙ |
| 22 % major (M1 / M2 > 1/3) mergers | |||
| 77 % minor (M1 / M2 < 1/3) mergers | |||
| fgas > 0.75 (for minor mergers) | |||
| S850 > 5 mJy duty cycle‡: 0.1 Gyr | |||
| Flat stellar IMF in starbursts | |||
| Chakrabarti et al. (2008) | gadget | Idealized Hydro | M* > 9.4 × 1011 M⊙ |
| radishe | Dust Radiative Transfer | necessary for S850 > 5 mJy | |
| Fontanot et al. (2007) | morgana | SAM | M* = 3.5 × 1011 M⊙ ∗‡ |
| Mhalo = 7 × 1013 M⊙ ‡ | |||
| fgas = 0.33 ‡ | |||
| SFR = 183 M⊙ yr-1‡ | |||
| Dekel et al. (2009a) | ramses | Cosmological Hydro (AMR) | ~ 1/2 of SMGs with S850 > 5 mJy |
| will be mergers with M1 / M2 > 0.1 | |||
| Davé et al. (2010) | gadget | Cosmological Hydro (SPH) | M* ≈ 1011 - 5 × 1011 M⊙ |
| Mhalo ≈ 6 × 1012 - 4 × 1013 M⊙ | |||
| 2% major (M1 / M2 > 1/3) mergers | |||
| fgas = 0.2 - 0.4 | |||
| SFR ≈ 180-570 M⊙ yr-1 | |||
| Somerville et al. (2012) | Santa Cruz | SAM | No Predictions Available∗ |
| Shimizu et al. (2012) | gadget | Cosmological Hydro (SPH) | M* = 5 - 35 × 1011 M⊙ ∗ |
| Mhalo = 1.4 - 10 × 1013 M⊙ | |||
| fgas = 0.7 - 0.8 | |||
| SFR = 250 - 1950 | |||
| Hayward et al. (2013b) | gadget | Hybrid | Physically Associated Galaxies: |
| Narayanan et al. (2010c) | sunrise | Dust Radiative Transfer | M* = 6 - 10 × 1010 M⊙ |
| Mhalo = 3 - 5 × 1012 M⊙ | |||
| SFR > 160 M⊙ yr-1 | |||
| Hayward et al. (2013a) | art | SAM | Physically Unassociated Galaxies (blends)∗: |
| Median M* = 9 × 1010 M⊙ | |||
| Median Mhalo = 5 × 1012 M⊙ | |||
| Median SFR = 190 M⊙ yr-1 | |||
| † We only include SAMs, hydrodynamic and hybrid models as they make bona fide predictions for physical quantities. | |||
| ‡ Median quantities for S850 > 5 mJy SMGs | |||
| ∗ Numbers obtained from authors via private communication. | |||
24 It should be noted that some subset of SAMs build upon analytic prescriptions that have been calibrated from large cosmological dark-matter only simulations, rather than via direct numerical simulation. Back.
25 Throughout, we refer to successors of a given code [e.g. gadget-2, gadget-3 by the base code name, and leave off the version number. Back.
26 A relatively up-to-date wiki describing both these codes, as well as a number of astrophysical codes is available at http://astrosim.net/code/. Back.
27 While the Fardal et al. (2001) work was never formally published, it appears on the arXiv, and is still referred to heavily in the theoretical SMG literature. Hence, we include it in our review. Back.
28 Note, that the term “major merger” is typically attributed to galaxies with mass ratio M1 / M2 > 1/3, rather than 0.1. Back.