5. REDSHIFT SURVEYS: GALAXY CLUSTERING

This chapter will discuss quantitative measures of galaxy clustering, and how we might use the results to put constraints on cosmological models for structure formation. Much of the background material has been introduced earlier in Section 2, although we will find ourselves introducing new concepts as we go along. We are not exhaustive in this section, and do not attempt to describe every statistic that has been used as a measure of galaxy clustering. In particular, we do not survey the work done with multi-fractal measures or percolation methods; these approaches have been thoroughly reviewed in this journal by Borgani (1995) .

We start with a discussion of the two-point correlation function (r) in Section 5.1. Before going onto the power spectrum in Section 5.3, we discuss the effects of redshift space distortions and non-linear effects in Section 5.2. Non-linear effects give non-zero high-order correlations, which we discuss in Section 5.4 and Section 5.5. Topological measures of large-scale structure are discussed in Section 5.6.

The dipole moment of the galaxy distribution is closely related to the motion of the Local Group (Section 5.7). One can expand the density distribution in higher-order multipoles as well, as discuss in Section 5.8. We return to the subject of redshift-space distortions with methods to correct for them in Section 5.9. We finish this chapter with a discussion of the relative distribution of different types of galaxies, in Section 5.10.

5.1. The Two-Point Correlation Function

The two-point correlation function was introduced in Eq. (44) as the autocorrelation function of the (continuous) density field. As it is the Fourier Transform of the power spectrum P(k) (Eq. 46), it also gives a complete statistical description of the density field to the extent that the phases are random. Although one can always define a smoothed density field as described in Section 3.7, and then apply Eq. (44), the resulting correlation function would be cut off on scales smaller than the smoothing length. Instead, we simply apply Eq. (45), which we rewrite as follows: the joint probability that galaxies be found at positions r₁ and r₂ within the infinitesimal volumes V₁ and V₂ is

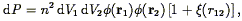
(81)

where r₁₂ = |r₁ - r₂|. In the case of a volume-limited sample ( 1) we thus find

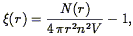
(82)

where N(r)r is the number of pairs found in the sample with separations between r and r + r, and 4 r² rn²V is the number expected in a uniform distribution of galaxies. This expression is appropriate only for the case of a volume-limited sample of galaxies, and ignores edge effects. In practice then, one does the following (Davis & Peebles 1983b): one generates on the computer a sample of points with no intrinsic clustering, but with the same selection criteria as those of the real galaxies. Thus the mock catalog matches the true catalog in the solid angle coverage and in the selection function. One then counts pairs with separation between r and r + r both in the real data (call this quantity N_DD(r), with D standing for data), and between the real data and the mock catalog (N_DR(r), with R standing for random). The correlation function is then estimated as:

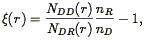
(83)

where n_D and n_R are the mean number densities of galaxies in the data and random samples. One usually makes the number of random galaxies much larger than that of the real sample so that additional shot noise is not introduced. In general, one can weight the pair counts any way one wants:

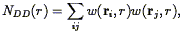
(84)

with a similar equation for N_RR, where the sum is over pairs of galaxies at positions r_i and r_j such that r < |r_i - r_j| < r + r. For flux-limited samples, weighting by the inverse of the product of selection functions for the two galaxies gives equal volume weighting. Saunders, Rowan-Robinson, & Lawrence (1992) show that the variance in (r) is minimized for the weights:

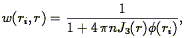
(85)

where J₃(r) was defined above (Eq. 62). Note that Eq. (85) bears a resemblance to the minimum variance weights for the mean density, Eq. (61).

The accuracy of Eq. (83) is limited by the accuracy of the estimate of the mean number density of galaxies; one cannot measure (r) on scales beyond that on which it falls below the fractional uncertainty in the mean density of the sample. The mean density is uncertain due to the possibility of large-scale structure on the scale of the survey itself. That is, one never knows the extent to which a given volume is a fair sample of the universe. The rms fluctuations in the density on the scale of a survey are given by Eq. (37), but of course, in order to estimate this, we need to know P(k), which is what we are trying to find in the first place. However, there exist estimators of (r) whose sensitivity to uncertainties in the mean density is appreciably weaker than that of Eq. (83) (Landy & Szalay 1993 ; Hamilton 1993b). In particular, Hamilton (1993b) shows that the fractional error in the estimator:

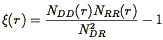
(86)

is proportional to the square of the fractional error in the mean density. This advantage of Eq. (86) over Eq. (83) actually only holds for weighting w(r_i) 1 / (r_i); otherwise, the two estimators give quite similar results. In any case, the differences between the two become apparent only on very large scales, where the correlation function is quite weak.

There has been a great deal of confusion over the proper estimation of the error in the correlation function. There are two sorts of statistical error one could try to calculate:

1. The difference between the true correlation function of galaxies in the volume surveyed, and that measured. This error arises from the finite number of galaxies in the sample.
2. Even if one could measure the correlation function in the volume surveyed without error, it will differ from the true correlation function of the entire universe of galaxies, due to power on scales larger than the sample.

Many of the analyses in the literature consider only one of these two effects. The problem is inherently difficult because the variance in the two-point correlation function necessarily depends on the three- and four-point correlation functions (to be discussed in Section 5.4). In addition, there exists strong covariance between the estimate of the correlation function on different scales, which of course is strongest for estimates at two closely spaced scales.

Peebles (1973) and Kaiser (1986) calculate the shot noise contribution to the correlation function errors in terms of a cluster model: if we think of the galaxy distribution as a smooth field with clusters embedded, the number of galaxies associated with each cluster is 1 + 4 nJ₃ (we restrict ourselves for the moment to the case of a volume-limited sample). The number of independent pairs of galaxies at a given separation is the number of observed pairs, N_DD, divided by the number associated with the clusters. That is, because galaxies are clustered, a majority of the galaxy pairs are redundant. The resulting error in the correlation function is then just given by Poisson statistics:

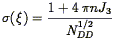
(87)

Kaiser (1986) notes that N_DD n², and thus for 4 nJ₃ >> 1, () is independent of n. Thus he argues that given a finite amount of telescope time, one wants to sparse-sample to the level that 4 nJ₃ 1 (i.e., roughly one galaxy per cluster), maximizing the volume covered to minimize the effect of power on scales larger than the sample. This is a meaningful strategy, if in fact one's primary motivation is to measure (r) on large scales. This is the motivation behind the 1-in-6 sampling of the QDOT survey (Lawrence et al. 1994), and the 1-in-20 sampling of the APM survey (Loveday et al. 1992a b).

Ling, Frenk, & Barrow (1986) argue that the effect of shot noise can best be estimated by making bootstrap realizations of a given sample, and calculating the scatter in the determination of (r) from each of these. Although the mean (r) over the bootstraps is unbiased, this results in an overestimation of the errors, as shown by Mo, Jing, & Börner (1993) and Fisher et al. (1994a) . Fisher et al. (1994a) describe a brute-force way to make realistic estimates of the correlation function error covariance matrix: make a series of independent N-body realizations of a given sample, and calculate the scatter of the estimates of (r) from each of these. Of course, this estimate will be only as good as the power spectrum assumed for the simulation itself, although it is probably not terribly sensitive to the details. Existing redshift surveys are not large enough to be able to afford to split the surveys up into pieces and compute errors from the variance in the estimated correlation function in each, although Hamilton (1993b) describes a practical method to estimate correlation function errors from one's dataset itself, by considering the contribution that each subvolume in a sample makes to the correlations.

The two-point correlation function can be applied not only to redshift data, but also to surveys containing only angular data. The angular correlation function can be defined in analogy with Eq. (81): the joint probability that galaxies be found at angular positions ₁ and 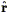₂ within the infinitesimal solid angles d₁ and d₂ is

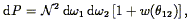
(88)

where ₁₂ is the angle between 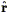₁ and 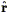₂, and 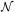is the number density of galaxies on the sky. Groth & Peebles (1977) calculated the angular correlation function of the Shane-Wirtanen Lick galaxy counts (cf., the beginning of Section 4); they found that w() is well fit by a power law of slope 0.77 for scales smaller than about 2°, with a sharp break on larger scales (cf, the challenge to their results by Geller, Kurtz, & de Lapparent (1984) and de Lapparent, Kurtz, & Geller (1986) over the issue of plate matching). More recently, the angular correlation function of the APM galaxies has been calculated by Maddox et al. (1990a) , who reproduce the Groth & Peebles (1977) results on small scales; however, the APM correlation function breaks on a somewhat larger scale than that of the Lick counts. The APM data are of higher photometric accuracy than the Lick data, and because the catalog was generated automatically it is immune from the inevitable systematic effects that counting galaxies by eye entails. Other recent determinations of the angular correlation function include Picard (1991) and Collins, Nichol, & Lumsden (1992) . Bernstein (1994) has carried out a detailed analytic analysis of the error in the angular correlation function (using the estimator of Landy & Szalay 1993), including the covariance terms, and using the hierarchical hypothesis (Eq. 120) to include the effects of three-point and four-point correlations. The resulting expressions are too complicated to reproduce here, but do an excellent job of matching the errors measured from Monte-Carlo simulations.

The angular correlation function w() for a flux-limited sample is related to the spatial correlation function by Limber's (1953) equation (cf. Rubin 1954):

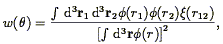
(89)

where is the selection function, r₁₂ |r₁ - r₂|, and is the angle between r₁ and r₂. It is straightforward to show from Eq. (89) that a power-law spatial correlation function of logarithmic slope corresponds to an angular correlation function with logarithmic slope - 1. Thus we expect the spatial correlation function to be a power law with slope = 1.77, at least on small scales. The spatial correlation function has been determined for essentially all the large redshift surveys discussed above in Section 3.1; important papers include Davis & Peebles (1983b) , Bean et al. (1983) , Shanks et al. (1983) , Davis et al. (1988) , de Lapparent, Geller, & Huchra (1988) , Strauss et al. (1992a) , Fisher et al. (1994a) , Moore et al. (1994) , and Loveday et al. (1995) . Because of the much smaller number of galaxies included in redshift surveys than in the angular catalogs, the spatial correlation function is determined with lower accuracy on large scales. However, these studies and others have demonstrated convincingly that the spatial correlation function is indeed a power-law on small scales, with a break at approximately 2000 km s^-1. The much quoted relation of Davis & Peebles (1983b) ,

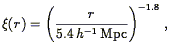
(90)

is consistent with the observed power-law behavior of w(). Eq. (90) also implies that the rms galaxy fluctuations within spheres of radius 8 h^-1 Mpc are unity (Eq. 37) ⁽¹⁶⁾ . This is a scale below which the clustering is clearly strongly non-linear, and much of the formalism developed in Section 2.2 becomes irrelevant.

A primordial power spectrum of power law slope greater than zero implies that P(0) = 0. It then follows from Eq. (46) that the volume integral of the spatial correlation function over all of space must be zero, meaning that the correlation function must go negative at some point. Given a power spectrum, for example, that of Standard Cold Dark Matter, one can use Eq. (46) to predict that the correlation function goes negative on scales above 33 h^-1 Mpc, and reaches a minimum at 46 h^-1 Mpc with an amplitude of -1.5 × 10^-3. This is too small an effect to have been measured in any existing galaxy sample. Indeed, if one defines the mean density of a sample from the sample itself (as is usually done), the integral of the correlation function over the volume of the survey is forced to zero. This effect tends to bias the correlation function low, at least when it is estimated for small volumes.

The power-law nature of the correlation function has prompted some workers to suggest that galaxies follow a fractal distribution, with no preferred scale (e.g., Coleman & Pietronero 1992). In such a model, it would not be possible to define a mean density of the universe; it would be a function of the scale on which one measured it. However, the correlation function is defined in terms of , which has the mean density subtracted already. The correlation function of 1 + predictably is not scale-free (e.g., Guzzo et al. 1991 ; Calzetti, Giavalisco, & Meiksin 1992). Peebles (1993) shows that the observed scaling of the angular correlation function with depth rules out simple fractal models (cf. Davis et al. 1988). More complicated, multi-fractal models have been proposed; they are reviewed thoroughly in Borgani (1995).

5.2. Distortions in the Clustering Statistics

The next logical topic to discuss would be the determination of the power spectrum of the galaxy distribution. Before we do so, however, we outline the principal effects which cause the observed correlation function and power spectrum to differ from those which held following the epoch of radiation-matter equality, extrapolated via linear theory to the present. These are:

1. The galaxy distribution may be biased with respect to the underlying mass distribution. If linear biasing holds (Eq. 48), the correlation function and power spectra of galaxies differ from that of the underlying dark matter by a constant factor b²; the shape of these functions is unaffected. However, if the biasing is a (a priori unknown) function of scale, then the power spectrum of galaxies gives us no information of that of dark matter.
2. We measure redshifts, not distances of galaxies. As Eq. (2) shows, the two differ from one another because of peculiar velocities.
3. Although in linear theory, the shape of the power spectrum does not change as clustering grows (simply because the growth rate is independent of scale), this is not true on scales that have gone non-linear, on which the rms mass fluctuations are not much less than unity.

We will discuss the redshift space distortions and the non-linear effects here.

5.2.1. Redshift Space Distortions

The effect of peculiar velocities on the shape of structures can be understood heuristically by imagining the gravitational influence of a rich cluster of galaxies. On small scales, within the virialized cluster itself, galaxies have peculiar velocities of 1000 km s^-1 or more, which causes a characteristic stretching of the redshift space distribution along the line of sight. This is called the " Finger of God", which points directly at the origin in a redshift pie diagram; the Finger of God associated with the Coma cluster is apparent in Fig. 3. Thus a compact configuration of galaxies is stretched out along the line of sight, greatly reducing the correlations: the small-scale velocity dispersion of galaxies causes the correlation function to be underestimated in redshift space.

On larger scales, a different effect operates: galaxies outside the cluster itself feel the gravitational influence of the cluster, and thus have peculiar velocities falling into it. A galaxy on the far side of the cluster will thus have a negative radial peculiar velocity, and appear closer to us in redshift space than in real space, while a galaxy on the near side will have a positive peculiar velocity, and appear further away from us. Thus the gravitational influence of a cluster causes a compression of structures, thus enhancing the correlation function.

These two effects can be quantified. The effect of the large-scale motions can be calculated via linear theory, as was first done in the present context by Kaiser (1987; cf. Sargent & Turner 1977). In brief, one calculates the change in the Jacobian of the volume element in going from real to redshift space. The result is that in linear theory, both the power spectrum and correlation function are enhanced in redshift relative to their real space counterparts by a factor:

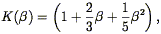
(91)

where was defined above in Eq. (51). For = 1, K = 1.87, so this is not a small effect. This calculation is done in the "distant observer approximation", in which the volume surveyed is supposed to subtend a small angle from the point of view of the observer. For further discussion of this approximation, see Cole, Fisher, & Weinberg (1994) , and Zaroubi & Hoffman (1994).

One way to disentangle the effects of peculiar velocities from true spatial correlations is to divide the vector separating any two galaxies into components in the plane of the sky (r_p in the notation of Fisher et al. 1994a), and along the line of sight (). The effects of redshift space distortions are purely radial, and thus the correlation function projected onto the plane of the sky is a measure of the real space correlation function. In practice, then, we measure _s as a function of both r_p and . The subscript s reminds that this is a quantity measured in redshift space. The projection of _s(r_p, ) onto the r_p axis yields a quantity closely related to the angular correlation function (Davis & Peebles 1983b):

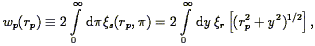
(92)

where here _r is the desired real space correlation function, as indicated by the subscript r. For a power-law correlation function _r(r) = (r / r₀)^-, the integral can be done analytically, yielding

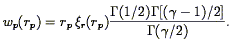
(93)

This is the approach that Davis & Peebles (1983b) took to find the result in Eq. (90); Fisher et al. (1994a) used this method to find

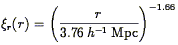
(94)

for IRAS galaxies. Saunders, Rowan-Robinson, & Lawrence (1992) measured _r(r) for IRAS galaxies using a related approach: they cross-correlated the QDOT redshift survey with its parent 2D catalog (Rowan-Robinson et al. 1991) to suppress the redshift spacing distortions; they find results in excellent agreement with Eq. (94) (cf. Loveday et al. 1995 for a measurement of the APM correlation function using the same technique). The significance of the discrepancy in the amplitudes and slopes between the IRAS (Eq. 94) and optical (Eq. 90) correlation functions will be discussed in Section 5.10.

If we could measure the Kaiser effect of Eq. (91) directly, we could constrain the parameter . The difficulty is that Eq. (91) is only valid on large scales where linear theory is valid, and where the competing effect of small-scale velocity dispersion is unimportant. But of course, the correlations are small and difficult to measure on these large scales. Gramann, Cen, & Bahcall (1994) and Brainerd & Villumsen (1994) point out that if the small-scale velocity dispersion were as large as predicted by standard CDM, then the Kaiser effect would be swamped by the suppression of the correlation function due to the velocity dispersion until one gets to truly enormous scales. Nevertheless, several groups have attempted to measure the Kaiser effect directly from redshift survey data. Fry & Gaztañaga (1993) compared the correlation function measured in redshift space for various redshift surveys to the angular correlation function of the same samples (which are free from redshift space distortions). They found = 0.53 ± 0.15 for the CfA survey, = 1.10 ± 0.16 for the SSRS, and = 0.84 ± 0.45 for the IRAS 1.936 Jy survey. Alternatively, one looks for the anisotropy of _s(r_p, ) in the radial and transverse directions. Hamilton (1992) defines the angular moments of the correlation function as

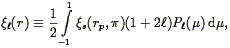
(95)

where P is the ^th Legendre polynomial and µ is the cosine of the angle between the line of sight and the redshift separation vector. He then shows that:

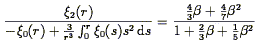
(96)

in the linear regime. Hamilton (1993a) applies this to the IRAS 1.936 Jy sample to find = 0.69^+0.28_-0.24.

Fisher et al. (1994b) took a somewhat different approach, including the effects of both the small-scale velocity dispersion and large-scale Kaiser effect, and fitting directly to _s(r_p, ). Following Peebles (1980) , the relation between the real and redshift space correlation functions can be written as

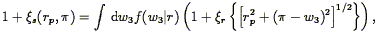
(97)

where the integral is over possible values of the radial peculiar velocity difference w₃, and f (w₃| r) is the distribution function of w₃ at a given separation r. An exponential distribution is a good approximation to the distribution function found in N-body simulations; Fisher et al. (1994b) show that it gives a better fit than does a Gaussian to the real data. Taking the shape of the first and second moments of f as a function of r from N-body models, Fisher et al. were able to reduce the model-fitting to two free parameters: the amplitude of the second moment (i.e., the pairwise velocity dispersion) at r = 100 km s^-1, and the amplitude of the first moment v₁₂ (i.e., the mean pairwise streaming of galaxies) at r = 1000 km s^-1. They show, in analogy with Eq. (91), that linear theory predicts the following form for the first moment:

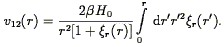
(98)

Thus the measurement of v₁₂ = 109⁺⁶⁴_-47 km s^-1 at 1000 km s^-1, together with the real-space correlation function (Eq. 94), directly yields a value for ; they find = 0.45^+0.27_-0.18. Although this statistic is shown to be unbiased with the help of N-body simulations, its power is limited by the volume of the sample. We assume that any anisotropy measured in the sample is due to redshift-space distortions, but the real space correlation function will be isotropic only to the extent that the sample includes enough volume to average over the orientation of elongated superclusters.

It is not a priori obvious that the approach of writing the effect of the redshift space distortions as a convolution with the velocity distribution function (Eq. 97) is consistent with linear theory in the form of Eq. (91); linear theory predicts covariance between the velocity and density fields that is not included in Eq. (97). However, Fisher (1995) has been able to reproduce Eq. (91) by expanding Eq. (97) to second order, assuming that f (w| r) is Gaussian, with mean value and dispersion as given by linear theory.

The Fisher et al. (1994b) analysis also measures the distortions on non-linear scales to derive the pair-wise velocity dispersion at 100 km s^-1, = 317⁺⁴⁰_-49 km s^-1. This is to be compared with the Davis & Peebles (1983b) value of 340 ± 40 km s^-1 from the CfA survey, also measured by looking at redshift space distortions ⁽¹⁷⁾ . The predicted values of for different power spectra (as calculated with N-body simulations) are quite different, so this quantity is of great interest for constraining models. High resolution dissipationless simulations of Standard CDM indicate ~ 1000 km s^-1 for the dark matter (e.g., Davis et al. 1985 ; Gelb & Bertschinger 1994b), far in excess of what is observed. However, this number has been controversial: it is the velocity dispersions of galaxies, not dark matter particles, which are observed. The velocity dispersion of halos of dark matter particles in simulations (Brainerd & Villumsen 1993; Gelb & Bertschinger 1994) are smaller than that of the dark matter itself, although these simulations suffer from the so-called over-merging problem, in which groups of galaxies merge in enormous supergalaxies, which have no counterparts in the real world. Because is weighted by pairs of galaxies, such over-merging tends to cause the estimate of to be biased low. Hydrodynamical simulations of CDM, which tend to avoid the over-merging problem, radiatively dissipate some of the energy that would otherwise go into galaxy motions, and in fact find a lower value for (e.g., Cen & Ostriker 1993), although still not low enough to match the observed value above. Weinberg (1994) shows that the velocity dispersion is very sensitive to the details of the biasing model used to define galaxies from the distribution of dark matter.

Velocity dispersion analyses of other redshift surveys (Mo et al. 1994) show a larger for some samples, although the pair-weighting nature of makes it quite sensitive to a few rare clusters in a survey volume (Zurek et al. 1994). What is needed to settle this controversy is a new statistic which is less weighted by the rare high velocity-dispersion clusters, and thus more strongly reflects the velocity dispersion in the field.

The small-scale velocity dispersion can also be used to apply the Cosmic Virial Theorem (Peebles 1976a , b; Peebles 1980): if one assumes statistical equilibrium of clustering on small scales, and takes the continuum limit, one can show that

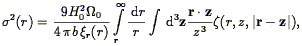
(99)

where is the three-point correlation function, to be discussed in Section 5.4. This equation can be simplified assuming a hierarchical model for the three-point correlation function (Eq. 118), and a power-law form for the two-point correlation function (Eq. 75.14 of Peebles 1980). In practice, the application of this equation is hampered by our poor knowledge of the three-point correlation function. More importantly, the linear biasing model assumed in Eq. (99) is questionable at best on these very inhomogeneous scales. Finally, Carlberg, Couchman, & Thomas (1990) argue that galaxies may not be fair tracers of the velocity field on small scales, a form of velocity bias. The Cosmic Virial Theorem has been used to argue for a small value of ₀ = 0.2e^±0.4 (Davis & Peebles 1983b), but if dark matter is not clustered with galaxies on the very small scales of 100 km s^-1, Eq. (99) will return an underestimated value of ₀ (Bartlett & Blanchard 1994).

Cole, Fisher, & Weinberg (1994) take a parallel approach to Hamilton (1992; 1993a), based on the power spectrum. Just as we can separate the vector between two galaxies into parallel and perpendicular components, we can separate a wave vector k into parallel and perpendicular components, if we work with a subsample of a survey with small total opening angle with respect to the observer, the distant observer approximation discussed above. In analogy with Eq. (95), they define angular moments of the power spectrum:

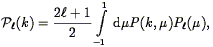
(100)

and show that the rational expression in Eq. (96) can be expressed as 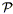₂(k) / 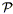₀(k). Applying this to the 1.2 Jy IRAS redshift survey, they find = 0.35 ± 0.05, although they emphasize that non-linear effects cause this to be a lower limit. A recent re-analysis by Cole, Fisher, & Weinberg (1995) parameterizes the effects of non-linearity in the velocity field by including a small-scale velocity dispersion in their model, in analogy to the analysis by Fisher et al. (1994b) . They find = 0.52 ± 0.13 for the IRAS 1.2 Jy sample, and = 0.54 ± 0.3 for the QDOT survey.

As in all these methods, non-linear effects have the potential to break the degeneracy between ₀ and b. Non-linear effects make the effective value of as derived from this method grow as a function of scale until the linear regime is reached; the scale at which the curve asymptotes is thus a measure of the strength of the mass clustering, and can be used to put constraints on the bias parameter. Unfortunately, existing redshift surveys are not extensive enough to measure this effect with confidence.

5.2.2. Non-linear Effects

In linear perturbation theory, the real space density field differs from the primordial density field only by a universal scaling factor. However, this is no longer true when non-linear effects become important. There has been a great deal of work in recent years on non-linear extensions to Eq. (30) (Bernardeau 1992a ; Gramann 1993a ; Nusser et al. 1991 ; Giavalisco et al. 1993 ; Mancinelli & Yahil 1994 ; cf. Mancinelli et al. 1994 for a comparison of these techniques), and various approximate non-linear schemes to bridge the gap between linear theory and N-body simulations (Peebles 1989a , 1990, 1994; Weinberg 1991 ; Matarrese et al. 1992 ; Brainerd, Scherrer, & Villumsen 1993 ; Bagla & Padmanabhan 1994). Here we wish to concentrate on methods to take redshift surveys back in time to their initial conditions. Weinberg (1989; 1991) adopts the assumption that the initial density distribution function is Gaussian, and notes that the rank order of densities is likely to be preserved even as non-linear effects skew the distribution function. Thus he applies a technique called Gaussianization, whereby the rank order of the densities at different points is conserved, but the densities are reassigned to fit a Gaussian form. The details of this method depend on assumptions about galaxy biasing and the power spectrum. The idea is to apply the Gaussianization technique to redshift survey data, measure the power spectrum of the resulting density field, and then evolve the resulting initial conditions forward in time again using an N-body code. To the extent that the assumed and measured power spectra match, and the final results agree with the original data, one has demonstrated consistency with the input model. Weinberg (1989) applied this technique on a volume-limited subsample of the Pisces-Perseus survey of Giovanelli & Haynes (1988) . The power spectrum was consistent with that of standard CDM. Unbiased models did not work, not reproducing the filamentary structure of the real data; b = 2 was a better match to the real data. Most importantly, the analysis tests, and finds consistency, with the assumptions of Gaussian initial conditions and gravitational instability.

Nusser & Dekel (1992) have developed a time machine to take the observed density field (as derived from a redshift survey or the POTENT method; cf. Section 7.5 below) back in time. The equations of motion allow a decaying mode (Eq. 26), which gets amplified if one simply reverses the density evolution equations. Nusser & Dekel (1992) instead start with the Zel'dovich equation (Eq. 34), which when expressed in Eulerian coordinates yields a first-order differential equation for the velocity potential which only allows a growing mode:

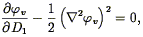
(101)

where _v is the potential associated with the scaled velocity field v v / a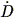₁. This Zel'dovich-Bernoulli equation can be integrated backwards in time from observations of the density fields; N-body tests show the results to reproduce the initial conditions better than does linear theory.

Gramann (1993a) shows that consideration of the continuity equation in the context of the Zel'dovich equation yields a correction term C_g to the right hand side of Eq. (101), given by:

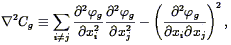
(102)

where _g is the gravitational potential. N-body tests show this equation reproduces the non-linear evolution better than does Eq. (101), although this approach has not been applied to redshift surveys yet.

Nusser & Dekel (1993) have used the Zel'dovich approximation in another version of their time machine. Assuming laminar flow, one can write down the eigenvalues of the space derivatives of the initial velocity field in Lagrangian space in terms of the eigenvalues of the space derivatives of the observed velocity field in Eulerian space ðv_i / ðx_i. Assuming further that linear theory holds in the initial conditions (as it should), one can derive the initial density field via Eq. (30); the final result is

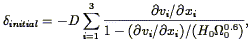
(103)

where D is the time dependence of the growing mode of gravitational instability (Eq. 27). They use the IRAS 1.936 Jy redshift survey and the methods of Section 5.9 to generate the predicted velocity field and thus the initial density field, from which they determine the initial density distribution function. They find it to be accurately Gaussian. Application of their technique to the observed velocity field is described in Section 7.5.1.

Another approach to non-linear gravitational evolution was taken by Peebles (1989a; 1990), and amplified by Giavalisco et al. (1993) . One can derive the exact equations of motion for a multi-body gravitating system by finding the stationary points of the action S:

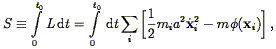
(104)

where the sum is over the particles in the system, m_i are their masses, x_i are their comoving positions, and is the gravitational potential. Giavalisco et al. then expand the positions x_i in a Taylor series, of which the Zel'dovich equation (Eq. 34) is the first two terms:

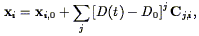
(105)

where the C_j,i are coefficients to be determined. Setting the derivative of the action S with respect to the C_j,i yields the set of equations

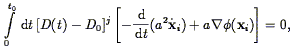
(106)

which can be solved for the unknowns C_j,i. This method is exact except in regions in which multi-streaming has occurred, that is, where a single point in Eulerian space corresponds to more than one point in Lagrangian space. Giavalisco et al. (1993) have tested this approach against spherical infall models, and show that it converges very quickly. Peebles (1989a; 1990) has used this method in the analysis of the dynamics of the Local Group, and the first attempts to extend this method to redshift surveys can be found in Peebles (1994) , and Shaya, Peebles, & Tully (1994) .

Hamilton et al. (1991) have taken an empirical approach to non-linear evolution of the power spectrum. Considerations of galaxy conservation within a radius r₀ fixed in Lagrangian space around a galaxy in an ₀ = 1 universe yields the hypothesis that the quantity a²J₃(r₀) / r₀³ is invariant with time, where J₃ is given by Eq. (62). Tests with N-body models show this in fact to be the case, and that this quantity is independent of the initial power spectrum, allowing the initial correlation function to be read off that measured. Using this method on the IRAS, CfA, and APM correlation functions allowed them to reproduce the initial correlation function, which they found to be best fit by a model invoking a mix of cold and hot dark matter. Extensions of their method can be found in Peacock & Dodds (1994) , discussed further below, and Mo, Jain, & White (1995) .

5.3. The Power Spectrum

In principle, the correlation function should contain all the information about the power spectrum, given that the two are a Fourier Transform pair (Eq. 46). However, there are two strong reasons to calculate the power spectrum directly from redshift surveys:

1. Determination of the correlation function on large scales depends on the calculation of the difference of two numbers close to unity (Eq. 83), while errors in the mean density of a sample affect the amplitude but not the shape of the power spectrum.
2. The error analysis and covariance between the determination of the power spectrum on different scales is more straightforward than for the correlation function.

The power spectrum can be calculated from a galaxy redshift survey as follows. The unsmoothed density field is given by a sum over Dirac delta functions:

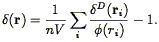
(107)

Taking the Fourier Transform of this yields

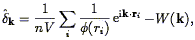
(108)

where

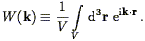
(109)

Our estimator of the power spectrum is then

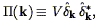
(110)

where the factor of V on the right hand side gets the units right. Several lines of algebra (Fisher et al. 1993) show that the expectation value of this estimator is given by

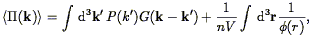
(111)

where

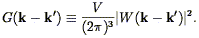
(112)

Thus the power spectrum estimator is given by the true power spectrum convolved with an expression involving the Fourier Transform of the volume, plus a shot noise term. In the limit of an infinitely large volume, G approaches a Dirac delta function.

The power spectrum as so defined is a function of the direction of k. In practice, one averages <(k)> over 4 steradians in k-space. Fisher et al. (1993) introduce the trick of measuring the power spectrum within cylinders embedded within the survey volume, whose long axis of length 2R is parallel to the vector k. If one then chooses kR = n with n a positive integer, the window function W vanishes (Eq. 109). This has two benefits: (k), and therefore the power spectrum now scale exactly with mean density, and thus errors in the mean density affect only the amplitude, and not the shape, of the power spectrum. In addition, the values of the power spectrum at different values of k are uncorrelated; there is no covariance between them.

Feldman, Kaiser, & Peacock (1994) have taken a slightly different approach. They include a weight function in Eq. (108), and derive an expression for the variance in the power spectrum estimator, assuming that the error distribution of P(k) is exponential (which follows from a Gaussian distribution of (r)). Minimizing the ratio of this variance to P² gives the optimum weight function for galaxy i:

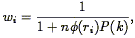
(113)

which is of a similar form to the optimum weight for the mean density (Eq. 61) and the correlation function (Eq. 85). With this weight function, the variance in the estimate of the power spectrum is given by

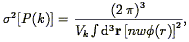
(114)

where V_k is the volume in k-space occupied by the bin in question. This expression assumes that the bins are spaced far enough apart that the covariance is negligible (this happens roughly for separations k > 2 / R, where R is the characteristic dimension of the volume surveyed). They also derive an expression for the off-diagonal terms of the covariance matrix; see their paper for details.

The power spectrum of galaxies has been calculated for a number of redshift surveys (Baumgart & Fry 1991 ; Peacock & Nicholson 1991 ; Park, Gott, & da Costa 1992, Vogeley et al. 1992 ; Fisher et al. 1993 , Feldman et al. 1994; Park et al. 1994 ; da Costa et al. 1994b; Lin 1995). Although there is reasonable agreement in the literature now about the shape of the power spectrum on small scales, its amplitude, especially on large scales, remains uncertain. The data are consistent with a slope of P(k) k^-1.4 on small scales, and several authors (e.g., da Costa et al. 1994b) show an abrupt change of slope at 2 / k = 50 h^-1 Mpc. All theoretical power spectra show a turnover on scales of 100 h^-1 Mpc or more (Fig. 2); this has not yet been seen unequivocally in the data. A number of authors (Peacock 1991 ; Torres, Fabbri, & Ruffini 1994 ; Kashlinsky 1992 ; Branchini, Guzzo, & Valdarnini 1994 ; Padmanabhan & Narasimha 1993 ) have derived empirical power spectra to fit the various data sets. The most thorough of these analyses is that of Peacock & Dodds (1994) , who have combined a number of the above datasets, together with the real-space correlation function (from the angular correlation function; Baugh & Efstathiou 1993 ). They correct each for the Kaiser effect (Eq. 91) on large scales, and the effects of small-scale velocity dispersion, following Peacock (1991) . Moreover, they correct for non-linear effects using the approach of Hamilton et al. (1991) (Section 5.2.2), extending the formalism to the ₀ 1 case. They combine the different samples, asking for consistency while adjusting five free parameters: four bias values (for Abell clusters, radio galaxies, optical galaxies, and IRAS galaxies), plus ₀, which determines the strength of the Kaiser effect (Eq. 91). They find that ₀^0.6 / b_IRAS = 1.0 ± 0.2. The small errors on this number imply that the redshift space distortion is unambiguously detected, largely based on the comparison with the real-space correlation function of Baugh & Efstathiou (1993) . The constraint on b_IRAS separately is less strong, but is consistent with unity. The ratios of the various bias factors are:

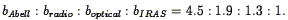
(115)

Their results on the reconstructed linear power spectrum are shown in Fig. 9. The points are means of the power spectrum from the various data sets, for ₀ = b_IRAS = 1. The two curves are standard CDM (dashed), and = 0.25 CDM, normalized to the power spectrum implied by the CMB anisotropies as measured by the COBE satellite (indicated by the box on the left-hand side of the figure). The data are clearly far more consistent with the = 0.25 CDM model than with standard CDM, both in amplitude and in shape (indeed, Peacock & Dodds come to this conclusion without consideration of the normalization afforded by the COBE data). This result is consistent with the conclusions of a number of workers in the field; we discuss the issues further in Section 9.1.

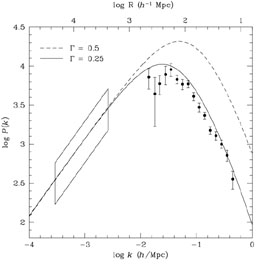
Figure 9. The power spectrum as derived from a variety of redshift surveys, after correction for non-linear effects, redshift distortions, and relative biases; from Peacock & Dodds (1994) . The two curves show the Standard CDM power spectrum, and that of CDM with = 0.25. Both are normalized to the COBE fluctuations, shown as the box on the left-hand side of the figure.

The second moment of the density distribution function is directly related to the power spectrum via Eq. (37). It can be calculated directly from redshift surveys as the second moment of the count distribution function (after correction for shot noise; cf., Peebles 1980 ; Saunders et al. 1991), and thus represents another handle on the power spectrum itself. This has been done by Efstathiou et al. (1990) , Saunders et al. (1991) , Loveday et al. (1992a) , Bouchet et al. (1993) , and Moore et al. (1994) , among others; the results they find are consistent with those shown in Fig. 9. A compilation of second moment results for IRAS galaxies is shown in Fisher et al. (1994a) . It makes the qualitative point that the variance drops as the scale increases, as is required by the Cosmological Principle, and follows for any power spectrum with n > - 3 (Eq. 39).

5.4. Higher-Order Statistics

As we have mentioned above, the power spectrum, or its Fourier Transform, the two-point correlation function, is a complete statistical description of the density field only to the extent that the phases of the Fourier modes of are random, implying that the one-point distribution function of the density field is Gaussian. Even if this condition holds for the density field in the early universe (as is predicted by inflationary models), it begins to break down as soon as non-linear effects start to develop. We discussed theoretical approaches to this problem in Section 5.2.2. In this and the following section, we discuss methods of measuring these non-linear effects from the data.

One can obviously extend the definition of the two-point correlation function to higher order. We can define the three-point correlation function for the continuous density field as

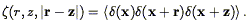
(116)

However, the practical definition in terms of the point distribution is more complicated, because of the need to correct for the contribution due to the fact that galaxies have a two-point correlation function. In analogy to Eq. (81), the probability of finding galaxies at distinct positions r₁, r₂, and r₃ within volume elements V₁, V₂, and V₃ is:

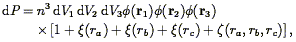
(117)

where r_a, r_b and r_c are the sides of the triangle defined by the three points. One can immediately see the difficulty in measuring , as it requires subtracting four terms from the triple counts. In addition, the three-point correlation function is now a function of three numbers, not just one. The problem only gets worse for higher-order correlation functions; the equivalent expression to Eq. (117) for the four-point correlation function has fifteen terms on the right hand side (Eq. 35.1 of Peebles 1980). Despite these difficulties, the three- and four-point correlation functions have been measured for the Shane-Wirtanen counts (Fry & Peebles 1978 ; Fry 1983 ; Szapudi, Szalay, & Boschan 1992), the CfA redshift survey (Bonometto & Sharp 1980; Gaztañaga 1992), and the IRAS samples (Meiksin, Szapudi, & Szalay 1992 ; Bouchet et al. 1993). These samples have measured non-zero three- and four-point correlation functions on small scales, indicating that the phases are indeed not random. More importantly, they have shown that the three- and four-point correlation functions display a certain symmetry with respect to the two-point correlation function:

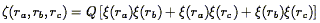
(118)

where Q is independent of scale and triangle configuration, to the level that the data can distinguish these things. In particular, there are no "loop terms", proportional to (r_a) (r_b) (r_c), which puts strong constraints on the form of biasing (e.g., Szalay 1988). A similar expression holds for the four-point correlation function. It has therefore been hypothesized that Eq. (118) can be generalized to the N^th order correlation function, indicated as _N (not to be confused with the of Eq. 95!). Balian & Schaeffer (1989) assume that the N-point correlation function shows scale invariance:

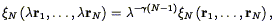
(119)

for any . They show that this allows one to write

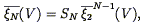
(120)

where the constants S_N uniquely define the hierarchical scaling, and the correlation functions averaged over a sphere are given by:

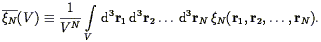
(121)

This volume-averaging integrates over the shape information in the high-order correlation function. Although there is much that can be learned from the dependence of the high-order correlations on the angles between the N points (Suto & Matsubara 1994 ; Fry 1994), the volume-averaged statistic is much more robust for small datasets. Moreover, the 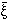_N(V) are equal to the irreducible N^th-order moments of the density distribution function: the skewness is 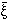₃(V) = <³>, the kurtosis is 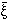₄(V) = <⁴> - 3<²>, and so on (Peebles 1980). For a power-law correlation function, the relation between (r) and its volume average can be calculated analytically (Peebles & Groth 1976):

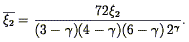
(122)

There has been a great deal of interest in recent years to calculate the hierarchy of S_N, both from the theoretical and observational sides. The use of volume averaging mitigates the need to calculate the N-point correlation function with its dependence on N(N - 1)/2 separations. In practice, one calculates the moments µ_N of the galaxy count distribution function, which are then corrected for shot-noise effects following Section 36 of Peebles (1980; cf. Szapudi & Szalay 1993 ; Gaztañaga & Yokohama 1993) to yield 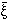_N. This only works for volume-limited samples, or angular data; flux-limited samples require a more elaborate correction (Saunders et al. 1991). One can then compare the observations with the predicted scaling, Eq. (120). As we will see momentarily, this scaling holds remarkably well, giving support to the scale invariant hypothesis (Eq. 19).

However, Eq. (19), or equivalently, Eq. (120), seems to have been pulled out of a hat. Before we show the observational evidence for them, let us discuss their theoretical motivation. For initial conditions with random phases, all S_N for N 3 are zero initially. However, as clustering grows and becomes non-linear, the density distribution function becomes non-Gaussian, and higher-order moments become non-zero. Peebles (1980) first calculated the skewness (i.e., third moment) of the unsmoothed density field in second-order perturbation theory for an ₀ = 1 universe, and showed that

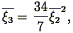
(123)

in agreement with Eq. (120). However, observationally, we are always limited to the smoothed density field, for which the quantity S₃ depends on the power spectrum (Juszkiewicz, Bouchet, & Colombi 1993):

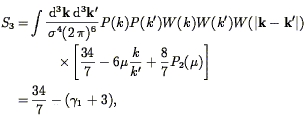
(124)

where µ is the cosine of the angle between k and k', W is the Fourier Transform of the window (cf. Eq. 38), and

(125)

where the derivative is calculated at the smoothing scale. Eq. (124) is valid for -3 ₁ < 1. The calculations get more difficult for increasing N; calculation of S_N requires the application of N - 1-order perturbation theory. One can show straightforwardly, however, that in every case, the scaling of Eq. (120) holds (Fry 1984a , b; Bernardeau 1992b). In a mathematical tour-de-force, Bernardeau (1994b) has set up a formalism for calculating the S_N for all N for a tophat window function, and presents expressions up to N = 7 as a function of the _i, I>i = 1, ..., N. It turns out that it is more difficult mathematically to do the calculations for Gaussian smoothing, although the cases N = 3 (Juszkiewicz et al. 1993) and N = 4 (Lokas et al. 1994) have analytic solutions. Analogous calculations have been done for the non-linear evolution of the power spectrum by Juszkiewicz (1981) , Makino, Sasaki, & Suto (1992) , Jain & Bertschinger (1994) and others. Feldman et al. (1994) examine the cumulative distribution function of |²(k)| in the QDOT data, and show it to be accurately exponential, as expected in a Gaussian field. However, the expected distribution in the mildly non-linear regime in the presence of shot noise has not yet been calculated.

The results quoted thus far are for an ₀ = 1 universe in real space. The dependence of the S_N on ₀ is extremely weak (Bouchet et al. 1992 , 1994), and is also insensitive to the transformation from real to redshift space. Moreover, it can be shown that the scaling relations Eq. (120), continue to hold under arbitrary local biasing transformations (Eq. 50), although the values of the S_N themselves change (Fry & Gaztañaga 1993 ; Juszkiewicz et al. 1995 ; Fry 1994). Biasing models which are non-local, in which the probability that a galaxy be formed at a given point is a function of events removed by tens of Mpc from that point, have been invoked to explain the mismatch of the observed power spectrum with Standard CDM (e.g., Babul & White 1991 ; Bower et al. 1993). However, such models break the scale-invariant hierarchy by adding loop terms (e.g., Szalay 1988), and Frieman & Gaztañaga (1994) have used the excellent agreement with the scale-invariant predictions (e.g., Fig. 10) to rule out a wide class of these models.

The calculation of S₃ and S₄ has been done for the CfA and SSRS samples (Gaztañaga 1992) and the IRAS 1.2 Jy sample (Bouchet et al. 1993), as well as for various angular catalogs (Szapudi, Szalay, & Boschan 1992 ; Meiksin, Szapudi, & Szalay 1992 ; Gaztañaga 1994 ; Szapudi et al. 1995). All these authors have found beautiful agreement with the predicted scaling relation: the results from the IRAS survey are shown in Fig. 10. Gaztañaga (1994) finds that the value of S₃ varies slightly with scale; this is expected by Eq. (124) if the power spectrum is not a pure power law. Inserting the power spectrum for the APM counts of Baugh & Efstathiou (1993) in Eq. (124) gives beautiful agreement with the observed values, implying that the biasing is very weak. This conclusion depends on the biasing being linear; non-linear biasing can mimic absence of biasing in the dependence of S₃ on scale.

Figure 10. The skewness (upper panel) and the kurtosis (lower panel) of the IRAS density field for various smoothing lengths, as a function of the variance. The plots are logarithmic. The lines drawn are least-square fits, with slopes 1.96 ± 0.06, and 3.03 ± 0.18, respectively. This figure is taken from Bouchet et al. (1993) .

Thus the scaling relations Eq. (120) were originally hypothesized on largely aesthetic grounds. They were found to be predicted by perturbation theory assuming Gaussian initial conditions, and growth of structure via gravitational instability. Indeed, calculations of the skewness in initially non-Gaussian models (Fry & Scherrer 1994 ; Bouchet et al. 1994) show that the leading behavior goes like 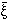₂^3/2, rather than 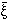₂² as observed. May we therefore conclude that we can rule out non-Gaussian models? Unfortunately, the answer is no. First, the 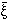₂^3/2 term decays with time, and at late times, may be negligible. Moreover, as many have quipped, referring to non-Gaussian models is a little like referring to non-elephant animals; the range of possible non-Gaussian models is vast. Weinberg & Cole (1992) set up a series of non-Gaussian models by skewing the density distribution function of an initially Gaussian model, but the resulting non-Gaussianity exists only on the smoothing scale on which is defined. On scales appreciably larger than this, the Central Limit Theorem guarantees that the distribution is Gaussian again, and the scaling laws between the various moments will continue to hold. Thus one needs to examine each specific non-Gaussian model in turn, ask for its predictions for the scaling either using analytic techniques or N-body simulations (Moscardini et al. 1991 ; Weinberg & Cole 1992), and compare with the data. This process has not been carried out in detail at this writing.

Finally, Fig. 10 shows that the scaling relation between the moments predicted by second-order perturbation theory holds well into the highly non-linear regime, where it has no right to hold (although this has been a working hypothesis for the closure of the so-called BBGKY equations; cf., Davis & Peebles 1977). Similar behavior has been seen in N-body simulations (e.g., Juszkiewicz et al. 1994). There is controversy about the effect of redshift space distortions in these analyses: Lahav et al. (1993a) , Suto & Matsubara (1994) , and Matsubara & Suto (1994) argue on the basis of N-body simulations that redshift space distortions make the S_N closer to constant than in real space in the non-linear regime, a conclusion supported by the analytic calculations of Matsubara (1994a) , and the observations of the Pisces-Perseus region by Ghigna et al. (1994) . However, Fry & Gaztañaga (1993) find that the S_N are remarkably constant in both redshift and real space on small scales, in a variety of redshift surveys. In any case, there exists no analytic argument as to why hierarchical scaling should hold into the non-linear regime.

5.5. The Density Distribution Function and Counts in Cells

One of the striking features of the galaxy distribution is the presence of voids as much as 6000 km s^-1 in diameter. The statistical tools that we have presented thus far do not clearly indicate their presence; we see no feature in the correlation function on such scales. Thus we look for a statistic that is more specifically oriented to describing the visible structures that we see. One such statistic is the void probability function. Imagine laying down a series of spheres of radius r randomly within a large volume populated with galaxies. Define the void probability function P₀(r) as the fraction of those spheres which contain no galaxies. In the absence of clustering, Poisson statistics yields

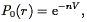
(126)

where n is the mean density of galaxies and V = 4 r³/3 is the volume of a sphere. In the clustered case, P₀ depends on the whole hierarchy of correlation functions, as shown by White (1979) :

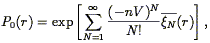
(127)

where the volume-averaged correlation functions were introduced in Eq. (121). Thus the void probability function is a complementary statistic to the correlation functions. One can compute not only P₀, but also the probability of observing N galaxies within a sphere; it is related to P₀ as:

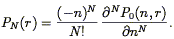
(128)

The void probability function is clearly a strong function of the sparseness of a given sample, and thus masks to a certain extent the underlying galaxy distribution. One way around this is to define a sampling independent quantity :

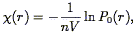
(129)

so that a Poisson distribution gives = 1 (Eq. 126). If the hierarchical hypothesis Eq. (120) holds, then Eq. (127) implies that is a universal function, independent of the sampling; indeed, this is observed for the IRAS galaxies (Bouchet et al. 1993 , but see Vogeley et al. 1991). (r) is observed to be a smooth monotonically decreasing curve with no features; no particular scale is picked out.

The void probability function is potentially a useful discriminant of cosmological models. However, Weinberg & Cole (1992) and Little & Weinberg (1994) found that the void probability function is insensitive to the power spectrum or the density parameter, and is more sensitive to the details of the biasing scheme than to the bias value itself.

Under the scale-invariant hypothesis (Eq. 19), one can make quite detailed predictions for the form of the P_N (Balian & Schaeffer 1989). Indeed, the density distribution function is given by (cf. Bernardeau & Kofman 1995):

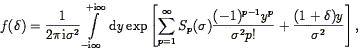
(130)

which is an exact expression to the extent that the S_p are exact ⁽¹⁸⁾ . The P_N follow from this after convolving with a Poisson distribution to include the effects of shot noise.

The various predictions developed by Balian & Schaeffer (1989) based on the scale-invariant hypothesis have been checked in N-body simulations (Bouchet et al. 1991; Bouchet & Hernquist 1992), although very dense sampling is required to test the full suite of predictions. The P_N have been derived observationally for various data sets (Alimi, Blanchard, & Schaeffer 1990 ; Maurogordato, Schaeffer, & da Costa 1992 ; Lahav & Saslaw 1992; Bouchet et al. 1993). The latter authors compare the observed counts in cells with various models, and find that a range of models (including those of Carruthers & Shih 1983 ; Saslaw & Hamilton 1984 ; Coles & Jones 1991) become degenerate at the sparse sampling of existing surveys, and the data cannot distinguish between them.

Another approach to the density distribution function (which is just P_N(r) at constant r) was introduced by Juszkiewicz et al. (1995) . On large scales, where the second moment of the distribution function ² <²> is small, the deviation of the distribution function from a Gaussian is expected to be small. Thus it makes sense to expand the distribution function in orthogonal polynomials relative to the Gaussian. The Edgeworth expansion does this:

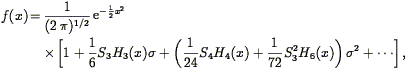
(131)

where the H_N(x) are the Hermite polynomials, and x = / . This is found to give an excellent fit to the distribution function in N-body models for small , although for 0.5 the Edgeworth expansion starts going unphysically negative at moderate values of x. Maximum-likelihood calculations of S_N using fits of Eq. (131) to the observed P_N may be more robust than calculation of the moments directly. Indeed, the results of the moments method are heavily weighted by the tails of the distribution. This is dangerous when working within a finite volume, because one is sensitive to the rare dense clusters (Colombi, Bouchet, & Schaeffer 1994 , 1995

We motivated this section by pointing out that standard correlation statistics do a poor job of quantifying the largest scale features that are apparent to the eye in redshift maps. The void probability function goes part of the way in filling this need, although it is not as discriminating a statistic between different cosmological models as was hoped. There have been a number of papers discussing various statistics to capture the largest-scale features apparent in the redshift maps (Tully 1986 , 1987a Broadhurst et al. 1990 ; Babul & Starkman 1992 , although again the robustness of these statistics, and their discriminatory power, have been questioned (Postman et al. 1989 ; Kaiser & Peacock 1991 . One of the most successful statistics to describe large-scale structure in a way complementary to correlation functions uses concepts from topology, to which we now turn.

5.6. Topology and Related Issues

What is the mental picture we should have of the topology of the galaxy distribution? Is it a uniform sea of galaxies punctuated by rich clusters embedded in it, like meatballs in a bowl of spaghetti? Dramatic voids are what catch the eye in Fig. 3; would a better picture be a uniform distribution with voids scooped out of it, like a piece of swiss cheese? If the density distribution is Gaussian, then there should in fact be a topological symmetry between underdense and overdense regions, like a piece of sponge. Motivated by these considerations, Gott, Melott, & Dickinson (1986) , who are responsible for these food analogies, suggested measuring the topology of the galaxy isodensity surfaces. In particular, given a surface in three-space, one can define the principal radii of curvature a₁ and a₂ at every point. By the Gauss-Bonnet theorem, the integral of the Gaussian curvature K 1 / a₁a₂ over the surface is given by

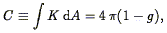
(132)

where g is the genus number of the surface (the number of holes minus the number of disjoint pieces, plus 1). Thus measurements of the Gaussian curvature give the genus of the surface. A plot of genus of the isodensity surface as a function of density thus tells us the change in the topology at different contrast levels. What do we expect in the Gaussian model? At very high density contrasts, the isodensity contours will surround isolated clusters, and thus the genus will be negative. Similarly, for close to -1, the isodensity contours will surround isolated voids, and again the genus will be negative. The mean isodensity contour will be multiply connected and sponge-like, and thus have a positive genus. One can calculate analytically the genus number in the Gaussian case (Doroshkevich 1970 ; Bardeen et al. 1986 ; Hamilton, Gott, & Weinberg 1987 ; cf. Coles 1988 for specific non-Gaussian models):

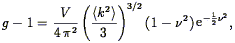
(133)

where V is the volume of the survey, = / is the level of the density in units of the rms of the density field,

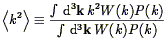
(134)

is the second moment of the smoothed power spectrum, and W(k) is the Fourier Transform of the smoothing window. Measurements of the genus as a function of thus characterize the general topology of the density field. In particular, we can test the Gaussian hypothesis by comparing the observed form to Eq. (133). To the extent that the observed genus curve is well-fit by the Gaussian form, the amplitude of the curve is a measure of the shape of the power spectrum at the wavelength of the smoothing. The amplitude of the power spectrum cancels out of Eq. (134). Gott and collaborators use a volume-weighting technique to reduce the sensitivity of the topology statistic to non-linear evolution and to separate the topological information from that carried by the density distribution function. Calculations of the genus curve from redshift surveys have been carried out by Gott et al. (1989), Moore et al. (1992) , and Vogeley et al. (1994) , using a tessellation technique for measuring the genus number (Gott et al. 1986; cf. Weinberg 1988 for the source code). Unfortunately, the volume of existing surveys is small, and thus for smoothing lengths in the linear regime, the maximum genus levels are ~ 20. The results show a slight "meatball" shift relative to the Gaussian case; that is, the overdense contours show larger values of g than Eq. (133) would predict. This is in the sense expected from non-linear evolution (Matsubara 1994b). The amplitude of the genus curve as a function of smoothing scale is in rough agreement with that predicted by CDM, although Moore et al. (1992) find some evidence for power in excess of CDM predictions on large scales. Statistical errors of the measurement of genus are usually calculated using bootstrap techniques, although these suffer from the same drawback as bootstraps for correlation functions (Section 5.1). At the moment, there is no rigorous error analysis of the genus statistic, nor any calculation of the effects of shot noise (which will tend to make the distribution function look more Gaussian). Very recently, Matsubara (1995) has studied the effect of redshift space distortions on the genus statistic.

A related statistic was invented by Ryden (1988) : the area of the isodensity surfaces. For a Gaussian field, one again expects a symmetric function, which again peaks at the mean density. The area is given by

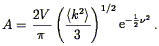
(135)

Ryden et al. (1989) invented a clever technique to measure this statistic, involving counting how often skewers put randomly through the survey volume intersect the isodensity surface, and applied this to the CfA survey and the Giovanelli & Haynes Perseus-Pisces survey. At 1200 km s^-1 Gaussian smoothing, the results closely matched the linear theory predictions. At 600 km s^-1 smoothing, however, the data showed stronger deviations from Gaussianity than did any of the models examined. However, their models were probably not evolved forward to become sufficiently non-linear on 600 km s^-1 scales; this remains a problem for further investigation.

5.7. The Dipole

One of the early motivations behind redshift surveys of the full sky was to apply Eq. (33) to the Local Group. The CMB shows a dipole anisotropy of amplitude T / T 10^-3 (Kogut et al. 1993, and references therein), which is interpreted as a Doppler effect due to the motion of the earth relative to the rest frame of the last scattering surface. When transformed to the barycenter of the Local Group following Yahil et al. (1977), this motion is 627 ± 22 km s^-1 towards l = 276 ± 3°, b = + 30 ± 3° (Galactic coordinates). Given a full-sky redshift survey, a comparison of this motion with the dipole moment of the galaxy distribution is a direct measure of . In fact, because both gravity and received light obey the inverse-square law, if one assumes a constant mass-to-light ratio for the galaxies, there is a direct proportionality between the peculiar velocity and the ratio of the dipole and monopole moments of the light distribution, allowing Eq. (33) to be applied using angular data only (Gott & Gunn 1973). The angular dipole moment of the galaxy distribution has been measured by a number of authors using a variety of galaxy catalogs (Meiksin & Davis 1986 ; Yahil, Walker, & Rowan-Robinson 1986 ; Villumsen & Strauss 1987 ; Lahav 1987 ; Harmon, Lahav, & Meurs 1987 ; Lahav, Rowan-Robinson, & Lynden-Bell 1988 ; Plionis 1988 ; Lynden-Bell, Lahav, & Burstein 1989 ; Kaiser & Lahav 1989 ; Scharf et al. 1992). The first impressive result of these analyses is that the vector direction of the light dipole agrees with that of the CMB dipole to within 10 - 30°, depending on the specific sample and analysis used. There is greater disagreement in the amplitude of the dipole, with results varying from = 0.3 to = 1.2. Rather than discuss the details of this here, let us move to the application of Eq. (33) using redshift surveys.

The first measurement of the gravitational dipole from a redshift survey was by Davis & Huchra (1982) , using a combination of the CfA and Revised Shapley-Ames (Sandage & Tammann 1981) surveys. Given the limited sky coverage of their sample, they were able only to measure the component of the acceleration towards the Galactic poles, which they compared to measured Virgocentric infall (Section 8.1.1), to find values of ⁽¹⁹⁾ ranging from 0.38 to 0.74, depending on exactly what assumptions were made. More recently, Pellegrini & da Costa (1990) combined redshift survey data from several different surveys, and carried out a similar comparison to the Virgocentric infall; they found in the range 0.24 to 0.56. Further progress had to await the completion of redshift surveys of the entire sky. The dipole moment of the IRAS QDOT redshift surveys was calculated by Rowan-Robinson et al. (1990) , who found convergence of the dipole only beyond 10,000 km s^-1. The amplitude of the dipole implied = 0.82 ± 0.15. Hudson (1993b) used his reconstruction of the optical galaxy density field to calculate the galaxy dipole; assuming that the dipole converges within 8000 km s^-1 allowed him to conclude that = 0.80^+0.21_-0.13.

We cannot simply calculate the right hand side of Eq. (33) given a redshift survey. The quantity that we do calculate is the dipole moment of the galaxy distribution:

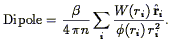
(136)

This differs from the dipole integral because of a number of effects, which we need to quantify:

1. Shot noise, which of course gets worse as the sample gets sparser at greater distances. In addition, Eq. (136) assumes a constant mass per galaxy, independent of the luminosity. It is straightforward to recast Eq. (136) in terms of luminosities, which is more appropriate for a luminosity measured in the optical than the IRAS bands (cf., Hudson 1993b). Appendix A of Strauss et al. (1992c) shows that the shot noise is a more important effect than mass-to-light ratio for all but the nearest galaxies.
2. The integral extends over all of space, while the galaxy dipole is necessarily measured through a window W(r), with cutoffs at both large and small distances, to minimize shot noise. Juszkiewicz, Vittorio, & Wyse (1990) , Lahav, Kaiser, & Hoffman (1990) , and Peacock (1992) point out that the contributions to the dipole due to material outside of the window can be substantial.
3. Eq. (33) assumes linear theory, while non-linear effects also come into play on small scales.
4. No redshift survey truly covers the whole sky. We discussed this issue in Section 3.8.
5. As Kaiser (1987) pointed out, redshift space distortions cause systematic errors in the derived dipole. In particular, if redshifts are corrected for a value of the Local Group peculiar velocity in error by an amount v, the derived dipole will have a spurious contribution (the rocket effect) given by

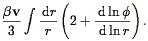
   (137)

Strauss et al. (1992c) develop a maximum likelihood analysis that allows them to take the first three of these effects into account. A power spectrum must be assumed in the analysis in order to quantify the effect of density fluctuations outside the assumed window. Indeed, one can include parameters of the power spectrum in the maximum likelihood analysis, although in practice, the constraints one can put on models are not very strong. The rocket effect is minimized using self-consistent solutions for the velocity field (cf. Section 5.9). The IRAS data imply = 0.55^+0.20_-0.12, where the angle between the acceleration and velocity vectors is 18 - 25°, depending on which self-consistent velocity field is used.

In models without large amounts of power on large scales, one expects the dipole to converge within the volumes probed by redshift surveys; that is, the contribution to the dipole on large scales should be negligible. The Strauss et al. results are consistent with the dipole converging within 4000 km s^-1, although this depends on which self-consistent density field is used, and how one corrects for the Kaiser effect. In addition, there is a substantial dipole moment contributed by galaxies between 17,000 and 20,000 km s^-1, aligned with the low-redshift dipole, although the sample is so sparse at those redshifts as to make this significant at only the 2 level. If this large additional contribution to the dipole is found at higher significance level with deeper redshift surveys, this will imply large amounts of power on large scales, and a smaller value of than inferred above.

5.8. Spherical Harmonics

An approach to quantifying the galaxy density field complementary to correlation functions uses the method of spherical harmonics. The Fourier components of the density field that are used in the power spectrum are orthonormal within a cube. Spherical harmonics are an orthonormal set of functions on a sphere, and thus are especially appropriate for full-sky samples. They offer a natural way to smooth the data; if one expands to a given order in l, the smoothing length is an increasing function of distance from the observer, mimicking the drop-off in the sampling in a flux-limited sample.

Spherical harmonics are simply the generalization to higher order of the dipole analysis discussed in the previous section. They have been used for many years to describe the distribution of galaxies in the celestial sphere, when redshift information was unavailable (Peebles 1973 ; Peebles & Hauser 1973 , 1974; Fabbri & Natale 1989 ; Scharf et al. 1992). One can express the galaxy density (, ) on the sky in spherical harmonics as

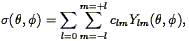
(138)

where the coefficients of the observed dataset are given by

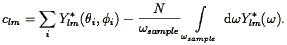
(139)

The sum is over the N galaxies in the sample, and the integral is over the solid angle subtended by the sample _sample. For an exactly full-sky sample, the second term vanishes.

The spherical harmonics can be related to the power spectrum straightforwardly. Scharf et al. (1992) show that the expectation value of the square of the coefficients in a Gaussian model with power spectrum P(k) is given by:

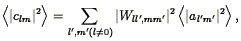
(140)

where

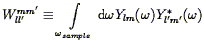
(141)

is a tensor which couples together different modes in the case of incomplete sky coverage, and the spherical harmonics in the case of complete sky coverage are given by

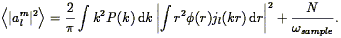
(142)

Scharf et al. (1992) used the angular distribution of the IRAS 1.936 Jy sample to put limits on the power spectrum, parameterized by an amplitude and a shape parameter, ₀h (Eq. 42). A maximum likelihood analysis yields ₀h = 0.25, ₈ = 0.8, with remarkably tight error bars.

Scharf & Lahav (1993) have extended this analysis using the redshift information of the 1.936 Jy sample as well. Much the same formalism is used, with the addition of a redshift weighting factor f (r) in the expansion of the density field (Eq. 138). In analogy to the dipole analysis described in the previous section, the growth of all the multipole moments with redshift is used as a diagnostic of the power spectrum. The resulting constraints on the power spectrum are similar to those which Scharf et al. (1992) found from the angular data alone, although Scharf & Lahav point out that redshift space distortions are a non-negligible effect.

Fisher, Scharf, & Lahav (1994) have calculated these redshift space distortions in linear theory. They find that the rms spherical harmonic amplitudes for a full sky redshift survey (i.e., _sample = 4 ), as measured in redshift space, is

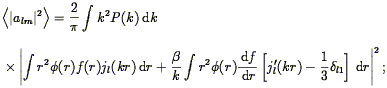
(143)

compare with Eq. (142). When measured for a real data set, there is of course an additional term due to shot noise. The dependence of Eq. (143) means that one can use the redshift distortions to measure , in exact analogy to the analyses of redshift space distortions of the correlation function and power spectrum. Of course, the shape and amplitude of the power spectrum also come into play; using a generic CDM spectrum (Eq. 42), Fisher (1994) finds = 0.94 ± 0.17 and = 0.17 ± 0.05. A similar analysis by Heavens & Taylor (1994) yields = 1.1 ± 0.3.

5.9. Recovering the Real Space Density Field

As we have emphasized throughout this review, redshifts are not equivalent to distances; the two differ due to peculiar velocities. However, to the extent that peculiar velocities are due to gravity, and that linear theory holds, we can use Eq. (33) to estimate these peculiar velocities. Of course, this requires knowledge of the density field, of which have a distorted view due to peculiar velocities. Thus we look for a self-consistent solution to the density and velocity field, given redshifts and positions for a flux-limited redshift survey of galaxies, and assuming a value of . In practice, this is doable only for full-sky redshift surveys, for which the integral in Eq. (33) can be carried out.

Yahil et al. (1991) describe an iterative technique to find this optimum solution. We describe it here in its latest incarnation (Willick et al. 1995d), as applied to the IRAS 1.2 Jy sample:

1. Galaxies are initially placed at their redshift space positions. The selection function is calculated by the methods of Section 3.4. The 10° wide zone of avoidance centered on the Galactic plane is filled with galaxies at a density interpolated from higher-density regions (Section 3.8).
2. A smoothed density field is defined by assigning the galaxies to a grid, weighting by 1/, and smoothing with a Gaussian using FFT's. The resulting density field is filtered with the power-preserving filter (Section 3.7), taking into account the increased shot noise as a function of distance from the origin.
3. Eq. (30) is solved for the velocity field, again using FFT techniques.
4. Given the density field (r) and velocity field v(r) along the line of sight 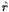to a given galaxy with Local Group redshift cz and flux f, one can calculate the probability P(r| cz, f )r that it have distance between r and r + r:

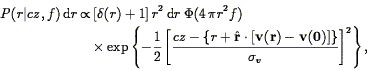
   (144)

   where is the galaxy luminosity function, v(0) is the peculiar velocity at the origin, and _v is a measure of the small-scale velocity dispersion not included in the smooth velocity field model. This method is inspired by the analysis discussed in Section 8.1.3 below. If the velocity field model were perfect, the exponential would be replaced by a delta function at cz = r + 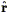. [v(r) - v(0)]; the Gaussian included here parameterizes our ignorance about the velocity field on scales smaller than the smoothing length. In the presence of clusters, there are regions in which the peculiar velocity changes with distance fast enough that one finds triple-valued zones, in which a given redshift can correspond to three distances. This is illustrated in Fig. 11, which shows the relation between redshift and distance along a line of sight which intersects a large cluster. Infall into the cluster causes the dramatic S-curve. A galaxy at a redshift of 1200 km s^-1 could lie at any of the three distances. The probability function of Eq. (144) is shown as well; it correctly parcels the probability among these three solutions. In particular, the nearest crossing point is most strongly favored, given the luminosity function weighting.

5. The density field is recalculated using the distribution function above and it and the velocity field are output. The value of is incremented on each iteration so that the effects of peculiar velocities grow gradually, the selection function is recalculated, and the iterations start again at step (iii) above.

This is the method used to generate Figs. 6 - 8 above. This basic approach of an iterated solution to the velocity field via Eq. (33) has been used by Yahil et al. (1991) , Strauss et al. (1992c) , Hudson (1993a, b), and Freudling et al. (1994).

Figure 11. An illustration of a triple-valued zone. The S-shaped curve shows the relation between redshift and distance along the line of sight to a cluster. A galaxy with a redshift of 1200 km s-1 can lie at three distinct distances. When the small-scale noise inherent in any velocity field model, as given by the scattered points, is taken into account, the distribution function of distances for a given redshift gets smoothed out, as shown as the three-peaked curve at the bottom.

Nusser & Davis (1994a) take a different approach to the problem. They point out that the difference between the redshift and real space position of galaxies is directly related to the displacement of a galaxy from t = 0 to the present (the Zel'dovich approximation, Eq. 34). Conservation of galaxies, and the assumption that the velocity field is irrotational, allows them to write down a Jacobian for the transformation from the initial conditions in real space to the final configuration in redshift space, which yields a differential equation for the velocity potential . Expanding and the density field (s) in redshift space on a given shell in spherical harmonics yields the equation:

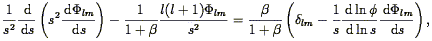
(145)

where is the selection function, and s is the redshift coordinate. This equation can be integrated for _lm using standard numerical techniques, and the radial velocity field can then be derived by differentiation. This method has the advantage that it does not require iteration (every term in Eq. (145) is in redshift space), but because it requires a one-to-one correspondence between real and redshift space, it does not allow the existence of triple-valued zones.

A similar approach is taken by Fisher et al. (1995) . They decompose the density field with spherical harmonics and spherical Bessel functions for the radial component:

(146)

They use the fact that for a survey with full-sky coverage, redshift space distortions couple only modes with a given l but with different n's, but there is no coupling between different angular modes. The coupling matrix is analytic, and its inverse allows the real space to be calculated from the redshift space , one spherical harmonic at a time. The velocity field then follows directly from Eq. (33). In practice, Fisher et al. (1995) use the Wiener filter to suppress shot noise. This method also does not require iteration. Fisher et al. (1994d) test the three methods presented here with the aid of a mock IRAS 1.2 Jy redshift survey drawn from an N-body simulation; all three give residual rms errors in the radial peculiar velocity field in the Local Group frame for galaxies within 6000 km s^-1 of 200 km s^-1. These comparisons have only been made at the positions of the galaxies used in the analysis; there is a need to compare the full velocity and density fields on a uniform grid.

Other approaches to real space reconstruction of redshift surveys include Kaiser et al. (1991) , Taylor & Rowan-Robinson (1994) , Gramann (1993b) , & Tegmark & Bromley (1994) .

5.10. Clustering of Different Types of Galaxies

Galaxy formation is a very poorly understood process. Our difficulties in understanding it stem both from our ignorance of the nature of dark matter, which presumably forms the potential wells within which the baryons that eventually form the stars of the galaxy fall, and the extreme complexity of the diverse hydrodynamic and stellar dynamic effects that become important as gas begins to radiate and stars form. In the context of this review, our principal concern is to gain some understanding of the relative distribution of the dark matter and galaxies, because it is the sum of the two which gravitates, while we can observe only the latter directly. In Section 2.4, we introduced the concept of biasing, and discussed the various contexts in which we might imagine that the distributions of galaxies and dark matter might differ. Here we ask how we might find observational evidence for biasing.

We observe that galaxies come in a variety of types, defined morphologically: from elliptical galaxies, through lenticulars, and then spirals both barred and unbarred, and finally irregulars and dwarfs of various sorts. If galaxies as a whole are biased relative to the dark matter, in the sense that the large-scale distributions of the two differ on large scales, one would expect that the process of galaxy formation caused the distribution of each of the galaxy types to be biased with respect to one another. Again, because galaxy formation is a poorly understood process, we do not have an accepted model for the Hubble sequence of morphological types, and we cannot be much more specific than this at this stage of our understanding. Nevertheless, this offers a well-posed observational problem: if we can measure biasing of one galaxy type relative to another, we have the potential of constraining biasing models.

One form of relative biasing has been known about since the time of Hubble: the cores of rich clusters are preferentially rich in elliptical galaxies. This was put on a firm quantitative basis by Dressler (1980a, b; 1984) and Postman & Geller (1984) , who showed that the relative fraction of elliptical galaxies rose from its mean of ~ 15% in the field starting at overdensities of ~ 200, to nearly unity in the highest-density regions of clusters. This means that redshift maps of elliptical galaxies in redshift surveys look qualitatively very different from those of spiral galaxies: the clusters are much more prominent in the former (cf. Giovanelli et al. 1986; Huchra et al. 1990a). This dramatic segregation of ellipticals and spirals does not extend into the field, but subtle relative biasing on large scales between the two have not yet been ruled out.

A number of workers have looked for such effects in the correlation statistics (Davis, Geller, & Huchra 1978 ; Giovanelli, Haynes, & Chincarini 1986 ; Santiago & da Costa 1990 ; Einasto 1991). One of the more powerful statistics for this purpose is the cross-correlation function ₁₂(r) for two populations of galaxies 1 and 2. The number of galaxies of type 2 within a shell a distance r from a galaxy of type 1 is n₂V[1 + ₁₂(r)]. One can compare the cross-correlation function with the auto-correlation function of either galaxy type; the ratio of the two is a measure of the relative bias of the two types of galaxies. This approach is especially appropriate when one of the two types of galaxies is quite a bit rarer than the other; the cross-correlation function is much more robust than the auto-correlation function of the rarer sample. The literature on searches for relative biases in different populations is vast: in addition to the morphology surveys discussed above, people have looked for segregation as a function of surface brightness (Davis & Djorgovski 1985 ; Bothun et al. 1986 ; Mo & Lahav 1993 ; Mo et al. 1994), luminosity (Hamilton 1988 ; Davis et al. 1988 ; Valls-Gabaud, Alimi, & Blanchard 1989 ; Thuan, Gott & Schneider 1987; Eder et al. 1989 ; Börner, Mo, & Zhou 1989 ; Salzer, Hanson, & Gavazzi 1990 ; Bouchet et al. 1993 ; Park et al. 1994 ; Loveday et al. 1995 , Marzke et al. 1994), emission-line properties (Salzer et al. 1988), and even mass (White, Tully, & Davis 1988). In addition, there have been comparisons of the distributions of galaxies selected in different wavebands, including IRAS vs. optical (Babul & Postman 1990 ; Lahav, Nemiroff, & Piran 1990 ; Strauss et al. 1992a), and radio vs. optical (Shaver 1991 ; Peacock & Nicholson 1991; Mo, Peacock, & Xia 1993).

The results of these various studies are often contradictory, but can be summarized as follows: on small scales, the correlation functions of late-type, lower surface brightness galaxies are weaker than that of early type galaxies by a factor of 1.5 to 2, depending on the exact sample used. There is also evidence that the later-type galaxies show a shallower slope. There is a similar relation between the IRAS and optical correlation functions (Eqs. 90 and 94); this is not surprising, given that IRAS galaxies tend to be late-type spirals. There is a weak dependence of the correlation strength on luminosity in both optical and IRAS bands, in the sense that more luminous galaxies show stronger correlation. This is worrisome, as it is a violation of the universal luminosity function assumption (Section 3.4). In particular, it means that clustering statistics derived from flux-limited samples will have systematic errors. The correlation function on small scales is heavily weighted by pairs of galaxies nearby, where the sampling is higher and thus there are more pairs. However, the nearby objects have lower luminosity in the mean than those galaxies further away, and if the correlations of the former are indeed weaker, the derived slope of the correlation function will be too shallow. With these effects in mind, some workers (e.g., Park et al. 1994) have restricted themselves to volume-limited samples in calculating clustering statistics from redshift surveys.

One of the most striking features of the observed galaxy distribution is the presence of voids. Models with little power on small scales have galaxies forming from the fragmentation of pancakes, and thus naturally predict voids. Explosion models (Ikeuchi 1981 ; Ostriker & Cowie 1981) naturally evacuate large regions of space in which galaxies will not form. Alternatively, models that exhibit strong biasing predict that very few galaxies form in underdense regions, naturally creating voids. However, one would expect that in these various scenarios, those few galaxies within voids should have different physical properties from galaxies in the denser regions (Dekel & Silk 1986 ; Hoffman, Silk, & Wyse 1992 ; Brainerd & Villumsen 1992). A number of workers have compared the redshift maps of bright galaxies with dwarf galaxies (Eder et al. 1989 ; Thuan, Gott, & Schneider 1987), low surface brightness galaxies (Bothun et al. 1986 ; Mo et al. 1994), emission-line galaxies (Salzer et al. 1988), HI-rich galaxies (Weinberg et al. 1991), and IRAS galaxies (Babul & Postman 1990 ; Strauss et al. 1992a); no distinct population of galaxies that "fills the voids" has yet been found. Alternatively, a number of workers have looked for distinguishing physical properties of those galaxies in voids and in more normal environments (Hoffman, Lu, & Salpeter 1992 ; Szomoru et al. 1995); no strong effects are seen, in contrast to the situation in clusters, where dramatic differences in mean galaxy properties are seen as a function of local density. Peebles (1989; 1993) argues that this lack of physical differences between void galaxies and those in mean density environments is a strong failing of the biasing model. Santiago & Strauss (1992) do a point-by-point comparison of the density fields as traced by different galaxy types in the CfA survey; the differences they see between ellipticals and spirals are statistically significant, with spirals being over-represented relative to ellipticals in the intermediate-density region ( 2) around the Virgo cluster. Confirmation of this result will require larger samples with more accurate Hubble types; this is one of the principal motivations of the Optical Redshift Survey (Santiago 1993 ; Santiago et al. 1995a , b).

¹⁶ Eq. (90) has been corrected for redshift space distortions; see Section 5.2.1. Back.

¹⁷ A recent reanalysis of the CfA sample by Davis (private communication) finds = 380 km s^-1 after correction of a small error in the original code. Back.

¹⁸ That is, if one wants a result accurate to N^th order, one needs the S_p, p < N calculated to N^th order as well; it is not adequate to calculate the S_p to lowest non-vanishing order. The higher-order corrections to the S_p have not yet been calculated. Back.

¹⁹ This paper was written before the concept of biasing was formulated, and so the results are quoted in terms of ₀, not . Back.