


In this review we distinguish between two basic approaches to modeling the galaxy–halo connection, empirical modeling, which uses data to constrain a specific set of parameters describing the connection at a given epoch or as a function of time, and physical modeling, which either directly simulates or parameterizes the physics of galaxy formation such as gas cooling, star formation, and feedback. A schematic summary of these approaches to the galaxy–halo connection is given in Figure 1, which gives an example of the galaxy and dark matter distributions for one such model, and outlines the key elements of various approaches. We note that in practice these modeling approaches are more of a continuum: as one moves to the right in this figure, one is assuming less physics directly from the model itself, and has more flexibility to constrain the unknown aspects of the galaxy–halo connection directly with data, but the models are also less predictive and less directly connected to the physical prescriptions. In general, approaches towards the right are also significantly less expensive computationally than the more physical approaches.
We begin in Section 2.1 by reviewing the concept of a dark matter halo. We then review current approaches to empirical modeling of the galaxy–halo connection in Section 2.2, including abundance matching, the halo occupation distribution and conditional luminosity function, and models which connect galaxies over time to their histories. In Section 2.3, we review approaches to physical modeling of galaxy formation, including hydrodynamical simulations and semi-analytic modeling, highlighting areas of synergy with empirical approaches.
2.1. Preliminaries: What is a halo?
In the modern theory of cosmological structure formation, dark matter halos are the basic unit into which matter collapses. Schematically, halos can be thought of as gravitationally bound regions of matter that have decoupled from the Hubble expansion and collapsed. In numerical simulations they are generally defined with masses and radii specified by a given overdensity: Mvir = 4π / 3 Rvir3 Δρm. The definition of Δ chosen in the literature varies (with values around 200); here unless otherwise specified we use the definition given by Bryan & Norman (1998), which characterizes the overdensity predicted for a virialized region that has undergone spherical collapse.
Within the radius of a dark matter halo there may be multiple, distinct peaks in the density field with virialized clumps of dark matter gravitationally bound to them. These subhalos are smaller than the host halo, and they orbit within the gravitational potential of the host halo. Resolving and tracking such objects is critical for making proper comparisons to the observed distribution of galaxies.
We note that the definition of halo radius given above, though common in the literature, may not be the most physically motivated definition of the boundary of a dark matter halo. Diemer, More & Kravtsov (2013) have emphasized that the commonly used definitions of halo boundaries can lead to unphysical interpretations about halo mass accretion histories. For example, measuring halo growth using Mvir will lead one to infer significant halo growth which is due just to the halo boundary being defined to larger radii with time, which they term “pseudoevolution”. Recently several authors have suggested an alternative concept, the “splashback” radius, which specifies the radius at which matter that is bound to the halo can orbit to after first collapse (Diemer & Kravtsov, 2014, More, Diemer & Kravtsov, 2015, Adhikari, Dalal & Chamberlain, 2014, Mansfield, Kravtsov & Diemer, 2017); this radius may also be more co-incident with the radius at which gas can shock heat, and at which infalling substructures can start being stripped by their host halos. Because this has not been yet widely adopted in most of the studies we review, we do not adopt this convention here, but we note that it may change some of the detailed physical interpretation of results presented (it is not expected to change the qualitative conclusions).
2.2. Empirical models of the galaxy–halo connection
The revolution in our understanding of the galaxy–halo connection has been driven by new physical insights as well as significant input from simple empirical models that connect observations from galaxy surveys to the predictions of the properties and evolution of dark matter halos in cosmological simulations. Here, we generally assume that the basic properties of dark matter halos are known for a given cosmological model. They can be predicted directly using an N-body simulation, or using fitting functions that summarize the properties of halos in such a simulation. To predict clustering statistics for example, one wants to know the abundance of dark matter halos (the “halo mass function”; see e.g. Sheth, Mo & Tormen 2001, Tinker et al. 2008b), their clustering properties (the “halo bias”; e.g. Sheth & Tormen 1999, Tinker et al. 2010, which can be a function of mass, redshift, and scale), the radial distribution of matter or substructures within halos, and the velocity distribution of dark matter or of substructures within halos. In most of the discussion below, we assume these predictions are made with gravity-only N-body simulations; we explicitly discuss the impact of hydrodynamics and feedback where relevant.
2.2.1. Abundance Matching. Perhaps the simplest assumption one could make about the galaxy halo connection is that the most massive galaxies live in the most massive dark matter halos. This basic approach is generally called “abundance matching” in the literature (the most massive galaxy lives in the most massive halo; the second most massive galaxy lives in the next most massive halo, etc.) The earliest versions of this assumption, applied before there were robust simulations that resolved cosmological structure within halos, assumed only one galaxy per halo (e.g. Wechsler et al., 1998, Colín et al., 1999, Kravtsov & Klypin, 1999, Moustakas & Somerville, 2002). However, CDM predicts structure on all scales, and thus predicts that dark matter halos host distinct substructures. These substructures (above a certain mass) are expected to host galaxies. A simple ansatz is thus that each halo and subhalo hosts a galaxy, with the mass or luminosity of a galaxy matched by abundance to the mass or velocity of the dark matter (sub)halo in which it lives; this is often referred to as subhalo abundance matching (“AM” or “SHAM”) in the literature (Kravtsov et al., 2004, Tasitsiomi et al., 2004, Vale & Ostriker, 2004).
Once this assumption is made, one can calculate a range of statistics for the model. Although the earliest versions of these models were sometimes referred to as zero parameter models, there are in fact a set of assumptions or parameters that need to be specified. The two most important are: (1) what halo property is best matched to what galaxy property? and (2) what is the scatter between these properties? It was realized quickly that while subhalos are rapidly stripped of their outer material after being accreted into a larger dark matter halo, galaxy stripping starts much later (Nagai & Kravtsov, 2005). Thus, one might expect a model which matches galaxies to halo properties at the time they are accreted into their host halos to provide a better match to a luminosity-selected galaxy sample; this was demonstrated by Conroy, Wechsler & Kravtsov (2006). Later work has investigated several alternative possibilities for the matching proxy, discussed further in Section 4.1. However, even in the presence of scatter between galaxy and halo masses, abundance matching is best thought of as a non-parametric technique that directly connects the stellar mass function to the halo mass function (Tasitsiomi et al., 2004). This can be done by deconvolving the scatter, as described by Behroozi, Conroy & Wechsler (2010); see in particular Section 3.3.1 of that work for the equations governing this deconvolution. 2 The consequences of and constraints on scatter are discussed further in Section 4.3. We note that modern versions of abundance matching models generally require high-resolution simulations; they depend on resolved substructure and on accurate merger trees to track the path of halos at least to the point in time that they started being tidally stripped.
2.2.2. The stellar mass/halo mass relation (SHMR). Abundance matching can be used to determine the typical galaxy stellar mass at a given halo mass, or galaxy stellar-to-halo mass relation, which we abbreviate as SHMR. An alternative to inferring this SHMR from non-parametric abundance matching is to parameterize it and constrain the parameters (e.g. Moster et al., 2010). The SHMR for central galaxies is shown in Figure 2, as constrained by non-parametric abundance matching, as inferred by a parametric SHMR constrained by abundance and clustering data, and as derived by a number of other methods that will be described below. The basic shape of this relation derives from the mismatch between the halo mass function and the galaxy stellar mass function or luminosity function, which declines rapidly below typical galaxies and has a much shallower faint-end slope than the halo mass function. One can see several clear features in this relation, which are identified consistently using any of the methods used to constrain it. First, the peak efficiency of galaxy formation is always quite low: if all halos are assumed to host the universal baryon fraction Ωb / Ωm of 17%, at its maximum, these results show that just ∼ 20–30% of baryons have turned into stars, resulting in a SHMR that peaks at just a few percent. This maximum galaxy formation efficiency occurs around the mass of halos hosting typical L* galaxies like the Milky Way, around 1012 M⊙; we refer to this as the pivot mass. At higher and lower masses, galaxy formation is even less efficient. Roughly, the stellar mass of central scales as M∗ ∼ Mh2−3 at dwarf masses and M∗ ∼ Mh1/3 at the high mass end. Images of typical galaxies that populate halos of a given mass are shown below the relation.
| SHMR : The stellar-to-halo mass relation. This can be predicted with models of galaxy formation, inferred from parameterized models, or measured directly. |
This decrease in the efficiency of star formation is a signature of strong feedback processes from the formation of stars and black holes. It is likely due to combination of a number of processes: at high mass, AGN feedback can act to heat halo gas and limit future star formation (Silk & Rees, 1998, Croton et al., 2006); at low mass, feedback from massive stars is believed to be important in driving winds that eject gas, or prevent it from coming into a galaxy (Dekel & Silk, 1986, Hopkins, Quataert & Murray, 2012); at even lower masses, galaxies can be too small to hold onto their gas during the reionization period around z ∼ 6 (Bullock, Kravtsov & Weinberg, 2000). We discuss the constraints on this relation in more detail in Sections 5 and 6, but here we note that many different techniques are telling the same basic story.
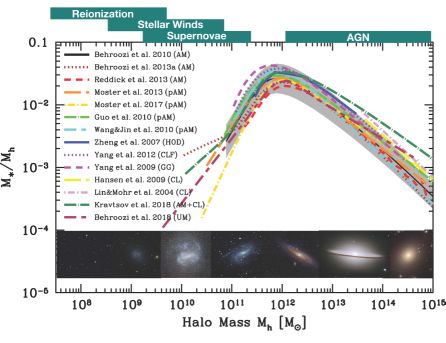 |
Figure 2. The galaxy stellar mass-to-halo mass ratio of central galaxies at z = 0. The figure (based on data compiled in Behroozi et al. 2018) shows constraints from a number of different methods: direct abundance matching (Behroozi, Conroy & Wechsler, 2010, Reddick et al., 2013, Behroozi, Wechsler & Conroy, 2013a); “parameterized abundance matching,” in which this relationship is parameterized and then those parameters are fit with the stellar mass function and possibly other observables (Guo et al., 2010, Wang & Jing, 2010, Moster et al., 2010, Moster, Naab & White, 2013); from modeling the halo occupation distribution (Zheng, Coil & Zehavi, 2007) or the CLF (Yang, Mo & van den Bosch, 2009) and constraining it with two-point clustering; by direct measurement of the central galaxies in galaxy groups and clusters (Lin & Mohr, 2004, Yang, Mo & van den Bosch, 2009, Hansen et al., 2009, Kravtsov, Vikhlinin & Meshcheryakov, 2018); and the “Universe Machine,” an empirical model that traces galaxies through their histories (Behroozi et al., 2018). Bottom panel shows example galaxies that are hosted by halos in the specified mass range. On the top of the figure, we indicate key physical processes that may be responsible for ejecting or heating gas or suppressing star formation at those mass scales. Figure adapted from Behroozi et al. (2018) with permission. |
Below some threshold halo mass, galaxies will no longer be able to form at all. The smallest known galaxies, ultra-faint dwarf galaxies, have measured dynamical masses in their inner regions larger than a few times 107 M⊙, which is most likely equivalent to halo virial masses of larger than 109 M⊙. The exact value of the minimum mass at which a halo can host a galaxy is still somewhat uncertain, as is the slope of and scatter in SHMR for halos below ∼ 1011 M⊙. Each of these has important consequences for understanding the lowest mass galaxies, and also has implications for the nature of dark matter (Bullock & Boylan-Kolchin, 2017).
We note that the SHMR generally parameterizes M∗ as a function of Mh. Due to scatter in these two quantities, quantifying the galaxy–halo connection with the mean halo mass in bins of M∗— as done observationally — does not yield the same mean relation. We discuss this in detail in Section 4.3.
2.2.3. The Halo Occupation Distribution and Conditional Luminosity Function. A popular way to describe the relationship between galaxies and dark matter halos is through the Halo Occupation Distribution (HOD), which specifies the probability distribution for the number of galaxies meeting some criteria (for example, a luminosity or stellar mass threshold) in a halo, generally conditioned on its mass, P(N|M). Typically this PDF is quantified separately for the central galaxies of halos and the satellite galaxies that orbit within the halos. For the former, a Bernoulli distribution is assumed, while for satellites a Poisson distribution is assumed. Under these assumptions the standard HOD is thus fully characterized by its mean occupation number ⟨ N|M ⟩; we discuss this assumption in Section 4.6. In principle, the HOD can be a function of properties other than halo mass; we discuss this possibility in Section 4.
| HOD : Halo occupation distribution. This specifies the probability distribution for the number of galaxies in a halo, generally conditioned on its mass, P(N|M). |
| CLF : Conditional luminosity function. This specifies the luminosity function of galaxies (both centrals and satellites) conditioned on halo mass. |
The connection between modern halo occupation models and measurements of galaxy clustering started to be explored by several workers in the early 2000s (e.g. Peacock & Smith, 2000, Seljak, 2000, Benson et al., 2000, Wechsler et al., 2001, Scoccimarro et al., 2001, Berlind & Weinberg, 2002, Bullock, Wechsler & Somerville, 2002), and is now well constrained for a wide range of galaxy samples. The functional form of the HOD for mass- or luminosity-selected galaxies is generally assumed to be similar to that of dark matter subhalos within their hosts. This was first studied in detail by Kravtsov et al. (2004), who found that the HOD for samples of subhalos is well-described by a power law of subhalos N ∼ M, with the addition of a central galaxy; for a given threshold on galaxy stellar mass, a typical central galaxy can be found in halos 10–30 times less massive than the halos that host satellite galaxies of the same stellar mass (examples are shown in the next section). This rough functional form has been shown to hold for luminosity-threshold or stellar mass-threshold samples of galaxies. In general, such an HOD can be described by 3–5 parameters for a given galaxy sample. Commonly used parameterizations are given in Zheng et al. (2005) (their equations [1] and [3]) and Reddick et al. (2013) (their equations 9 and 10). For more complicated galaxy samples (e.g. selected by star formation rates, colors, or emission lines), the functional form of the HOD can be significantly more complicated (e.g., Skibba & Sheth 2009).
The conditional luminosity function (CLF) and conditional stellar mass function (CSMF) go one step further to describe the full distribution of galaxy luminosities for a given halo mass. It is generally described separately by the distribution of central galaxy luminosities P(Lc|M) and satellite galaxy luminosity functions Φ(Lsat|M). This can be inferred directly from measurements of groups and clusters (Lin, Mohr & Stanford, 2004, Weinmann et al., 2006, Yang, Mo & van den Bosch, 2008, Hansen et al., 2009, Yang, Mo & van den Bosch, 2009) or from a full model for galaxy clustering and abundance (Yang, Mo & van den Bosch, 2003, Cooray, 2006). In general, this parameterization distinguishes between central galaxies, which are usually assumed to follow a lognormal distribution of stellar masses or luminosities at fixed halo mass, and satellite galaxies, which are usually assumed to follow a Schechter function (Schechter, 1976) whose parameters scale with halo mass. A concise review of the equations governing the CLF can be found in Section 3.7 of van den Bosch et al. (2013).
For both the CLF and the HOD, model predictions can be made in two ways. Both models specify the number of galaxies per halo, thus one can populate halos identified in an N-body simulation using a Monte Carlo approach, and ‘measure' observables from the resulting mock galaxy catalog. Alternatively, both of these frameworks can be combined with an analytic halo model of dark matter clustering to make predictions for some statistics analytically (see, e.g., Tinker et al. 2005 and van den Bosch et al. 2013). The CLF and HOD parameterize the galaxy–halo connection differently, but in spirit they quantify the same thing. Either method can be used to quantify the other (see, e.g., Leauthaud et al. 2011).
2.2.4. Empirical Modeling of Galaxy Formation Histories. Somewhat intermediate to the abundance matching and HOD/CLF models that describe a galaxy population at a fixed epoch and the full semi-analytic approach described in Section 2.3.2 is a class of models that trace galaxies within their dark matter halos over time, but directly constrain the galaxy–halo connection at each epoch. Conroy & Wechsler (2009) developed a simple approach along these lines using abundance matching at each epoch to determine the SHMR, combined with the typical mass accretion histories to connect halos through time, to determine typical galaxy accretion histories and star formation histories across cosmic time. Behroozi, Wechsler & Conroy (2013a), and Moster, Naab & White (2013) extended this work using simulated mass accretion histories (following on earlier work from Yang et al. (2012) with analytic approximations for halo properties) as well as updated constraints from the evolution of the galaxy stellar mass function and galaxy star formation rates to put strong constraints on the typical trajectories of galaxies through time.
This approach is being taken further by many workers (Becker, 2015, Rodríguez-Puebla et al., 2016, Cohn, 2017, Moster, Naab & White, 2018, Behroozi et al., 2018); instead of parameterizing the connection between galaxy stellar mass and halo properties at a given epoch, one can parameterize for example the relationship between the galaxy star formation rate and the halo mass accretion rate, and then trace these histories through time using simulated merger histories. This is a powerful approach which allows one in principle to use a range of data to constrain the model, and to make predictions for the distribution of galaxy star formation histories as well as their statistical properties at any epoch. In general this approach also requires high-resolution simulations to construct robust merger trees of dark matter halos and to trace the evolution of subhalos.
2.3. Physical models of galaxy formation
Physical models of galaxy formation attempt to either directly simulate or to model the basic physical processes in galaxy formation. The current status and approaches of these models, including both hydrodynamical simulations and semi-analytic models, were recently reviewed by Somerville & Davé (2015). Here we primarily focus on the connection to and contrast with empirical models, as well as the interplay between these various approaches.
2.3.1. Hydrodynamical Simulations. Hydrodynamical simulations model galaxy formation by solving the equations of gravity and hydrodynamics in a cosmological context, incorporating such processes as gas cooling, stellar-feedback driven winds, and feedback from black holes and supernovae, and in some cases magnetic fields and cosmic rays, and tracing the properties of dark matter, gas, and stars in given resolution elements over time. Although they contain extensive physical prescriptions, they cannot simulate the full range of scales needed for galaxy formation in a cosmological context without some parameterizations below the resolution scale, generally termed “subgrid physics.” These subgrid physics parameterizations need to be tuned, either through direct tests with observations or by comparison to constraints with empirical models that connect observations to dark matter halos.
Although there is still significant uncertainty in the details, there has been dramatic progress in producing realistic galaxy populations in hydrodynamical simulations over the past decade, due to increasing resolution as well as improved physical models for star formation and feedback, based on insight from a wide range of observations. These models provide our best understanding of the complex interplay between the physical processes of galaxy formation, and they can thus be used to inform and test the assumptions of empirical models. The earliest studies of the halo occupation in hydrodynamical simulations were performed before it was well-constrained by empirical models (White, Hernquist & Springel, 2001, Pearce et al., 2001, Berlind et al., 2003), following earlier work looking at the occupation in a semi-analytic model by Benson et al. (2000). These studies provided useful insight into early modeling approaches for the HOD, e.g. Zheng et al. (2005) used smoothed particle hydrodynamics simulations and semi-analytic models to propose forms for the HOD and CLF that were later constrained with the best-available clustering data from the Sloan Digital Sky Survey. More recently, Simha et al. (2012) and Chaves-Montero et al. (2016) have tested the key assumptions of the subhalo abundance matching approach with modern cosmological hydrodynamical simulations.
The interplay goes both ways: in recent years, measuring the galaxy–halo connection either through the SHMR or the halo occupation in these simulations and comparing to constraints obtained from empirical models and/or combinations of data has become a standard test for cosmological hydrodynamical simulations and semi-analytic models (Genel et al., 2014, Vogelsberger et al., 2014, Schaye et al., 2015). Because these models are computationally expensive (generally, at least an order of magnitude more CPU time to simulate a given volume than dark matter only simulations), the SHMR and other parameterizations of the galaxy–halo connection provide very useful intermediate targets that can be easier to match than full forward modeling of the entire galaxy population and comparing directly to the range of observables that have been used to constrain it. This can be done for full cosmological simulations e.g. Crain et al. (2015), or one can even run a small set of high-resolution resimulations and evaluate whether the typical galaxy mass agrees with that inferred from empirical models (Stinson et al., 2013, Munshi et al., 2013). Below, we review comparisons between these models and current empirical constraints.
2.3.2. Semi-analytic models of galaxy formation Semi-analytic models of galaxy formation (White & Frenk, 1991, Kauffmann, White & Guiderdoni, 1993, Somerville & Primack, 1999, Cole et al., 2000, Bower et al., 2006, Guo et al., 2013) aim to model the same basic processes of galaxy formation in a computationally efficient manner, by approximating the various physical processes with analytic prescriptions that are traced through the merging history of dark matter halos. In current models, these prescriptions are most often traced through merger trees extracted from N-body simulations. Although these models are significantly less computationally expensive than hydrodynamical simulations, they generally have a large number (10–30) of parameters and fully exploring this parameter space has remained a challenge. These prescriptions also necessarily make simplifying assumptions, that need to be continually tested both with full hydrodynamical simulations and with data. Several recent studies have used Monte Carlo Markov chain techniques to directly constrain the semi-analytic model parameter space with data (Henriques et al., 2009, Lu et al., 2011, Lu et al., 2014, Henriques et al., 2015). Fully constraining these models with clustering data and other spatial statisics is still challenging due to the large parameter space and computational expense. As an alternative, the SHMR and other aspects of the parameterized galaxy–halo connection can provide useful intermediate steps to test the agreement of models with a wide range of data.
| SAM : Semi-analytic model |
2.4. Complementarity between approaches
One of the most encouraging aspects of the current state of galaxy formation modeling is that each of the approaches outlined above is increasingly being used to inform the others: more direct physical models can be used to inform and test the parameterizations and assumptions of empirical approaches, and empirical constraints can be used to efficiently synthesize diverse constraints from data and pin down uncertainties in the physical parameterizations. At present, due to the computational expense of more physical models, empirical models also are more widely used in studies that jointly constrain the galaxy–halo connection with cosmological parameters. Empirical models are also important for cases in which one wants to marginalize over possible uncertainty in the galaxy–halo connection in order to robustly infer cosmological parameters or uncertain dark matter physics.
2 A code to implement this procedure is available at http://bitbucket.org/yymao/abundancematching Back.