8. DISSIPATIONAL GALAXY FORMATION

Whether galaxies form via the collapse and fragmentation of massive adiabatic fluctuations or by the clustering and merging of low mass isothermal fluctuations, dissipative processes may provide the key to understanding many of their observed properties. These include the luminosity function, metallicity gradients, and correlations between global parameters. In this Section, we review the role and implications of dissipation in hierarchical clustering theories (Sections 8.1 and 8.2) and in the pancake theory of galaxy formation (Section 8.3). In Section 8.4 we describe a theory in which galaxies form by the coagulation of small clouds which may be applicable in both hierarchical and pancake theories. The role of pregalactic stars is considered in Section 8.5 where we briefly review a new class of galaxy formation schemes in which density fluctuations on the scales of galaxies and clusters are generated by astrophysical processes operating after recombination.

8.1. Characteristic dissipative mass-scales

It is first useful to establish a general criterion for dissipation to play a general role in galaxy formation. Simple comparisons of cooling and gravitational time-scales lead to some interesting indications of characteristic protogalactic scales (Hoyle, 1953; Binney, 1976b; Rees and Ostriker, 1977; Silk, 1977a). We assume a primordial abundance mixture of hydrogen and helium. The cooling rate coefficient in a diffuse ionized gas at T 2 × 10⁴ K may then be approximated by

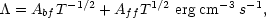(8.1)

where A_bf is the bound-free cooling coefficient (and is weakly temperature dependent) and A_ff is the free-free cooling coefficient. There are separate contributions to A_bf from H and He, although only He cooling is important at T > 5 × 10⁴ K. Detailed computations of the coefficients A_bf and A_ff may be found in Cox and Tucker (1969). The cooling time-scale is written

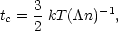(8.2)

and is approximately proportional to T^3/2 n^-1 for T 10⁶ K and T^1/2 n^-1 for T 10⁶ K.

We compare t_c with the collapse time of a uniform pressure-free sphere

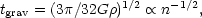(8.3)

and note that we can write

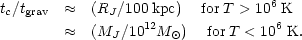(8.4a) (8.4b)

Here R_j = ( kT / µ G )^1/2 is the Jeans length and M_J = R_J³ / 6. We conclude that an initially uniform and spherically symmetric collapsing cloud will first be able to cool once it has collapsed within a radius of 100 kpc if T > 10⁶ K or if its mass is less than 10¹² M if T < 10⁶ K. Silk (1977b) and Rees and Ostriker (1977) have made the interesting point that the characteristic scales given in Eqs. (8.4) may be expressed, to order of magnitude, in terms of fundamental physical constants,

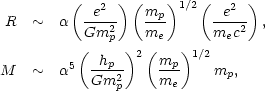(8.5a) (8.5b)

where is the fine structure constant = 2 e² / (h_p c)]. For comparison, the mass of a star is [h_pc / (Gm_p²)]^3/2 m_p. These equations neatly illustrate how it may be possible to interpret the characteristic masses and radii of galaxies in terms of astrophysical processes that are independent of the details of the cosmological model (e.g. H₀, or the photon entropy per baryon). This contrasts with other characteristic mass scales that we have mentioned, such as the damping mass for adiabatic fluctuations (Eq. 4.12), the neutrino Jeans mass (Eq. 5.21) or the Jeans mass just after recombination (Eq. 5.26).

To decide which of these two limits is appropriate, we must examine the role of pressure. Since the initial collapse is adiabatic (t_c > t_grav), we have T ^2/3. Now a reasonable guess for the initial temperature is T_i 10⁴ K. Thus to attain T > 10⁶ K at R > 50 kpc requires collapse from > 500 kpc where the density is only < 10^-4(M/10¹² M) cm^-3 compared with the mean density in the universe n 10^-5(1 + z)³ h² cm^-3. We conclude that the mass limit is the more realistic one. Thus only mass-scales below ~ 10¹² M can cool effectively. This compares rather well with the luminous masses of the brightest galaxies, an L^* galaxy having a luminous mass of ~ 3 × 10¹¹ M.

The preceding argument applies to uniform spherical collapse. A straightforward generalization suggests that inhomogeneous collapse can be similarly constrained if we compute the critical surface density for a shock between two colliding clouds to be radiative. This quantity depends only on the shock strength, and effectively only on the relative velocity dispersion of the colliding clouds. Again at low velocities, it is equivalent to an upper limit on mass and at high velocities to a bound on radius. This approach will be discussed in detail in Section 8.4.

At large redshifts Compton scattering of electrons by the background radiation provides an important cooling mechanism. The Compton cooling time-scale is

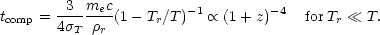(8.6)

Clearly Compton cooling is effective within a collapse time if t_comp < t_grav, which yields

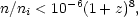(8.7)

where n_i is the mean density of a cloud that just begins to recollapse at redshift z. Hence only after the density increases by a factor 100 at z = 10 or 10¹⁰ at z = 100 will atomic cooling processes dominate. The necessary collapse factor is so large at z = 100 that rotational forces are likely to become important: recall that v_rot / n^1/6 for a self-gravitating collapsing cloud that conserves its angular momentum. At low redshift (z 10), Compton cooling will not affect the arguments which led to Eq. (8.4). However, at high redshift (z >> 10), the predominantly Compton cooling is scale-independent: all mass-scales collapse in free-fall until star formation or rotational forces intervene. These arguments are summarized in Figure 8.1.

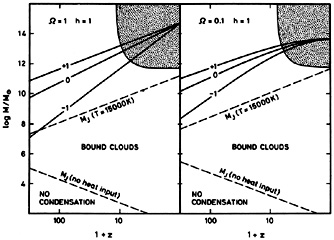Figure 8.1. The lines separating the shaded regions show tc / tgrav = 1. Gas clouds in the shaded region cannot cool on a free-fall timescale. Compton cooling, which is scale independent, is dominant at z 10. The criterion of Eq. (8.4b) is applicable at z 10. We also show, for three values of the primordial power-spectrum index [n = + 1, 0, - 1, Eq. (5.9)], the evolution of the characteristic mass scale (Mnl) for proto-lumps that are just entering the non-linear regime of gravitational clustering. This is matched to the present day galaxy correlation function which indicates Mnl 5 × 1014 h-1[r0 h/4 Mpc]3 M. Bound clouds would be expected to lie below these lines. If there is no heat input after recombination, the Jeans mass falls as (1 + z)3/2 so bound systems cannot have formed below this line. Clouds can form and remain in virial equilibrium in the region between the dashed lines (adapted from Rees and Ostriker (1977), with permission).

An important extension of these ideas has been proposed by White and Rees (1978). They point out that any acceptable model for galaxy formation must take into account the large amounts of "missing mass" known to exist in rich clusters of galaxies and, probably, in dark halos around spiral galaxies. Any theory which attempts to explain galaxies by dissipationless collapse would seem to be unable to explain why the mass-to-light ratios of rich clusters [M/L ~ 400h(M/L)] are so much larger than the mass-to-light ratios deduced for the material within the optical radii of galaxies [M/L ~ 10h(M/L)]. Fall (1981) has expressed this problem in an interesting way. A typical L^* galaxy has a half-light radius r_1/2 ~ 3 kpc and a luminosity overdensity with respect to the background of

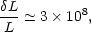(8.8a)

(using Eqs. 2.19 and 2.22). If, however, galaxies formed without dissipating any binding energy, the mean luminosity overdensity should coincide with the mean mass overdensity inferred from the galaxy two-point correlation function,

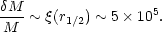(8.8b)

The discrepancy between (8.8a) and (8.8b) is roughly a factor of 10³ indicating that typical galaxies have collapsed by a factor of ~ 10 in radius.

White and Rees propose the following model. Most of the material in the universe is assumed to be dark in order to account for the high M/L values of rich clusters. The exact nature of the dark material is unimportant. Any of the usual candidates such as low mass stars, the remnants of supermassive stars, or weakly interacting particles (e.g. gravitinos, photinos, etc., see Section 9) would be acceptable. The important point is that the dark material must be in a form which does not dissipate energy. Primordial gas, destined to form the luminous parts of galaxies, accounts for only a small fraction of the mean mass density of the universe (~ 1 - 10%). The dark material, therefore, provides the dominant contribution to the gravitational potential and can cluster hierarchically in the manner described in Section 5.3. The gas, on the other hand, can radiatively cool and dissipate binding energy to form the dense luminous components of galaxies. The requirement that this could have happened on a time-scale shorter than the Hubble time, using a slight modification of the cooling arguments described above, again leads to a characteristic mass scale similar to Eq. (8.4b). Under some fairly specific assumptions, White and Rees show how the cooling arguments can lead to a galaxy luminosity function that is in reasonable agreement with observations [Eqs. (2.18) and (2.19)].

In summary, the White and Rees theory predicts that each galaxy should have formed within the potential well of a dark halo and that the largest galaxies should have masses ~ 10¹² M. The high over-densities and low mass-to-light ratios of galaxies are accounted for if the gas collapses dissipatively by a factor of ~ 10 in radius before fragmenting into stars. Systems with masses > 10¹² M would produce groups and clusters, rather than individual galaxies and should have high mass-to-light ratios. This is because cooling processes cannot lead to segregation of dark and luminous material on these scales. On scales larger than individual galaxies, therefore, the galaxy correlation functions should accurately trace the mass distribution. In the next section we consider the role of angular momentum in the White and Rees theory.