8.2. Angular momentum and dissipative collapse

In Section 6.3 we showed that the tidal torque theory for the origin of angular momentum is inconsistent with the idea that spiral discs formed by the dissipative collapse of a self-gravitating gas cloud. The White and Rees theory offers an interesting way out of this difficulty (Efstathiou and Jones, 1980; Fall and Efstathiou, 1980).

Although some aspects of the theory are inevitably rather vague, one that appears to be on fairly safe ground is the expectation that the total angular momentum per unit mass of the gas destined to form a disc should be equal to that of the dark halo material:

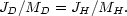(8.9)

This is because all the material in the system experiences the same external torques and violent relaxation before separating into two distinct components. The numerical simulations discussed in Section (6.3) predict that a typical system will have a pre-collapse value of the dimensionless spin parameter of = 0.07. The goal is now to compute the factor by which the protocloud must collapse in order to produce a centrifugally supported disc. We assume that the equilibrium disc has an exponential surface density profile,

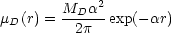(8.10)

and a flat-rotation curve with amplitude v_m which we parametrize by the dimensionless ratio,

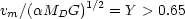(8.11)

where the constraint Y > 0.65 is required so that the halo density be everywhere positive. Thus the disc's angular momentum is,

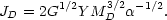(8.12)

We now assume that disc self-gravity may be neglected. Thus, the halo density profile must be of the form,

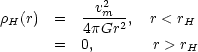(8.13)

in order to produce a flat rotation curve. Equations (8.11) and (8.13) thus give,

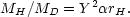(8.14)

Now,

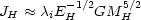where _i is the pre-collapse spin-parameter of the system and E_H is the total energy of the halo component. Since the halo component collapses without dissipation we may compute E_H from (8.13) and since angular momentum is conserved, the collapse factor of the disc component, r_H, may be fixed from Eqs. (8.9) and (8.12). This gives,

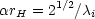(8.15)

and is independent of the parameter Y. Thus, if _i = 0.07 we find r_H 20, which is an order of magnitude smaller than the prediction of Eq. (6.26) and is compatible with the requirement that the collapse time be considerably less than the age of the Universe and with observational arguments which suggest that the disc collapsed by a factor of ~ 10. A detailed computation, using a more realistic rotation curve and which does not neglect the self-gravity of the disc, is given by Fall and Efstathiou (1980). Their results are summarized in Figures 8.2(a, b). Notice that their results are well fitted by Eq. (8.15) for r_H 10.

The fraction of the total mass of a galaxy in the halo component is given by Eq. (8.14). However, this depends on the parameter Y which cannot be directly determined from observations of disc galaxies. Theoretical arguments concerning the stability of disc galaxies suggest that Y ~ 1 (Efstathiou, Lake and Negroponte, 1982) in which case M_H / M_D r_H 20 if _i = 0.07.

The available data are thus consistent with the general picture in which dark material and gas collapsed simultaneously to produce disc-halo systems. The collapse factors and mass factors predicted by White and Rees agree remarkably well with those necessary to explain the rotation of disc galaxies by tidal torques. However, the slow rotation observed in giant elliptical galaxies does not have such a natural explanation within the framework of the White-Rees theory. The mass-to-luminosity ratio within a de Vaucouleurs' effective radius, r_e, is observed to be M/L 14h(M/L) for typical giant ellipticals (Section 2.1D). This is far less than the M/L values of rich clusters but comparable to the M/L values within the Holmberg radii of spiral discs. In order to explain these observations, one infers that giant ellipticals must have collapsed by a factor of ~ 10, similar to the collapse factor required for the formation of a disc galaxy. It is, therefore, difficult to understand why giant ellipticals are observed to rotate so slowly, with ~ 0.07, similar to a typical pre-collapse value of the spin parameter from tidal-torques.

Figure 8.2. (a) Pre-collapse spin parameter as a function of collapse factor rt (Fall and Efstathiou, 1980). In these models the disc is assumed to have a rotation curve of the form where = (1/2 rm)2 ( MD G / vm2). The self-gravity of the disc material is taken into account. The narrow shaded region is appropriate for models with parameters in the indicated ranges. The dashed lines show the 10, 50 and 90 percentile values of the tidal spin distribution found in N-body experiments (Efstathiou and Jones, 1979). (b) Halo-disc mass ratio as a function of collapse factor rt and the parameter Y = vm / ( MD G)1/2 for the models of Figure 8.2(a). Arguments based on disc stability would suggest that Y 1.1 whilst a naive application of Larson and Tinsley's (1978) stellar population models gives Y ~ 0.8.

One possibility (Kashlinsky, 1982) utilizes the broad distribution of the -parameter from tidal torques (cf. Figures 8.2a) to argue that ellipticals form from proto-clouds which collapse in halos with unusually low pre-collapse values. Another possibility (Hogan, 1979) is that a pregalactic generation of massive stars that formed soon after recombination may have photoionized the remaining gas. The ionized gas will remain coupled to the background radiation by Compton drag whilst the stellar component (ultimately to become the dark material) can continue to cluster hierarchically. The gas can only collapse when the sources expire, or when Compton drag becomes ineffective at z_c 140( h²)^1/5, whichever happens first. Because the gas remains locked to the comoving frame whilst it is ionized, tidal torques will not operate on the gas. Thus when Compton drag ceases, the gas will have a lower specific angular momentum than the dark material (violating the assumption of Eq. 8.9) and may be able to dissipate a large fraction of its binding energy yet still produce a slowly rotating elliptical.

A major difficulty with either of these suggestions lies in accounting for the observation that ellipticals occur predominantly in rich clusters of galaxies. In Kashlinsky's picture it is difficult to see how the spin-parameters of proto-galaxies could be correlated on the scales of galaxy clusters at the time of galaxy formation. Whilst in Hogan's picture, Compton drag becomes ineffective at a relatively high redshift, when a rich cluster was still a small density perturbation.

Several authors (Fall, 1979b; Efstathiou and Jones, 1980; Silk and Norman, 1981) have pointed out that galaxy mergers might resolve the problem of forming ellipticals in the White-Rees theory. As we have seen above, there seems to be little difficulty (at this level!) in accounting for spiral discs. Thus we can argue that all proto-clouds collapse and form disc galaxies. Ellipticals then form from mergers between disc systems. In this way, we might hope to account for the correlation between morphological type and environment, the fraction of elliptical galaxies relative to spirals and the rotational properties of ellipticals. The extent to which the merger scheme can account for these facts has been reviewed in detail in Section 7, so we will not repeat the discussion here. Suffice it to say that a good deal more work needs to be done before we have a final answer.