


8.4. Cloud coagulation and galaxy formation
We have seen that pancake theories lead to formation of clouds of
subgalactic scale at z < 10. Isothermal fluctuations
lead to clouds with mass somewhat in excess of the Jeans mass at
recombination, 105.8
 -1/2
M
-1/2
M .
The clouds cluster hierarchically to eventually build up into
systems of galactic mass. On either picture, clouds must avoid
catastrophic cooling and gravitational collapse and survive for a
period of at least 108 yr, the minimum dynamical
time-scale for
forming a galaxy. Internal star formation provides the most likely
means of stabilizing these clouds. Only if the clouds are
predominantly gaseous at the epoch of galaxy formation can one account
for many of the observed features of galaxies.
.
The clouds cluster hierarchically to eventually build up into
systems of galactic mass. On either picture, clouds must avoid
catastrophic cooling and gravitational collapse and survive for a
period of at least 108 yr, the minimum dynamical
time-scale for
forming a galaxy. Internal star formation provides the most likely
means of stabilizing these clouds. Only if the clouds are
predominantly gaseous at the epoch of galaxy formation can one account
for many of the observed features of galaxies.
Both of the extreme viewpoints described above,, involving either
hierarchical clustering or pancake collapse, result in the formation
of clouds of characteristic mass 106 - 109
M .
These are the precursors
of the galaxies. The idea that a protogalaxy consists of a collection
of interacting gas clouds is not new: it has formed a central role in
such models as those of
Peebles and Dicke (1968),
Larson (1974b), and
Gott and Thuan (1976).
Earlier discussions have, however, glossed over
a simple point, namely the physical mechanism by which such primordial
clouds are supported against collapse and ensuing fragmentation and
star formation.
.
These are the precursors
of the galaxies. The idea that a protogalaxy consists of a collection
of interacting gas clouds is not new: it has formed a central role in
such models as those of
Peebles and Dicke (1968),
Larson (1974b), and
Gott and Thuan (1976).
Earlier discussions have, however, glossed over
a simple point, namely the physical mechanism by which such primordial
clouds are supported against collapse and ensuing fragmentation and
star formation.
To illustrate this problem, let us note that the free-fall time of a
self-gravitating spherical cloud of mass
M6  M/106
M
M/106
M and virial temperature
T4
and virial temperature
T4  T/104 K (including both thermal and turbulent
contributions) is 9 ×
106 M6 T4-3/2
yr, whereas the time-scale over which
cloud aggregation occurs during galaxy formation is
T/104 K (including both thermal and turbulent
contributions) is 9 ×
106 M6 T4-3/2
yr, whereas the time-scale over which
cloud aggregation occurs during galaxy formation is
 108 yr, the
dynamical time-scale for a typical galaxy. In order for the clouds to
remain gaseous, avoiding cooling and collapse, an internal energy
source is required. A similar problem is encountered for interstellar
molecular clouds, whose lifetimes significantly exceed collapse
time-scales. Ongoing low-mass star formation apparently provides a
substantial momentum and energy input via protostellar winds
(Norman and Silk, 1980),
and it is logical to assume that a similar phenomenon
can energize the primordial clouds.
108 yr, the
dynamical time-scale for a typical galaxy. In order for the clouds to
remain gaseous, avoiding cooling and collapse, an internal energy
source is required. A similar problem is encountered for interstellar
molecular clouds, whose lifetimes significantly exceed collapse
time-scales. Ongoing low-mass star formation apparently provides a
substantial momentum and energy input via protostellar winds
(Norman and Silk, 1980),
and it is logical to assume that a similar phenomenon
can energize the primordial clouds.
It is, of course, necessary to demonstrate that primordial star
formation is not disruptive and, moreover, can be self-regulating.
One can show that even the coherent action of successive supernovae
need not destroy clouds of mass
106 - 107
M within 109 yr,
if the supernova rate is taken to be proportional to the star formation rate
and constant in time
(Silk and Norman, 1981).
In principle, one might
expect the star formation rate to be self-regulating; as the
energizing pre-main-sequence phase ends for most massive stars, the
cloud can cool, begin to collapse, and make more massive stars, which
in turn inhibit further collapse for some 106 -
107 yr. In this manner,
several generations of stars can form and evolve.
within 109 yr,
if the supernova rate is taken to be proportional to the star formation rate
and constant in time
(Silk and Norman, 1981).
In principle, one might
expect the star formation rate to be self-regulating; as the
energizing pre-main-sequence phase ends for most massive stars, the
cloud can cool, begin to collapse, and make more massive stars, which
in turn inhibit further collapse for some 106 -
107 yr. In this manner,
several generations of stars can form and evolve.
The characteristic mass of the first generation of stars must be several solar masses in order to avoid an excess of low metallicity stars at present. The primordial clouds will inevitably become enriched, since whatever the slope of the initial mass function, some extremely massive stars will have evolved, although the amount of enrichment is very uncertain and possibly variable from cloud to cloud. This suggests that galaxies form from an aggregation of pre-enriched gas clouds containing a considerable number of stellar remnants as well as surviving stars of lower mass. Theoretical arguments suggest that once the enrichment of a cloud exceeds that of extreme Population II, stars will form with a more or less conventional mass function (Silk, 1980). After substantial numbers of low mass stars have formed, the gas reservoir will rapidly be depleted. The end product of the evolution of such an isolated cloud may resemble a globular star cluster.
In the inner regions of a protogalaxy, frequent collisions between clouds will inevitably occur. One can consider two regimes. First, in the core of the galaxy, direct collisions between clouds result in coalescence of the gas if the collision occurs at sufficiently low velocity. Any embedded stars will be released, however. Suppose shocked gas is stimulated to form additional stars; one expects that a cloud cannot survive more than one or two collisions before the gas supply is exhausted. Outside the core, dynamical interactions between clouds are likely to be more important than direct collisions, and the cloud distribution will undergo violent relaxation following the initial collapse of the system. In regions of high galaxy density, mergers between protogalaxies will refuel the cores with a fresh supply of clouds.
In isolation, a protogalaxy gradually dissipates its kinetic energy via cloud-cloud collisions. The cloud collision-dominated core, defined by the condition tcoll < tdyn where tcoll is the cloud-cloud collision time-scale and tdyn the local dynamical time, and formed by violent relaxation of the cloud distribution, will rapidly form stars as collisions release existing stars and form new stars. This inner region constitutes the central bulge. The newly formed stars whose formation is triggered by cloud collisions will preferentially be produced towards the inner bulge regions because of the loss of kinetic energy in the collisions: consequently a metallicity gradient develops.
Unfortunately, the physics of dissipative collapse is so complex that any direct attack via hydrodynamical studies is doomed at the outset. The amount of freedom in modelling supersonic turbulence and star formation is practically unlimited: when gravity is incorporated, any feasible problem degenerates to a parameter study, with little physical content. Nevertheless, one gleam of optimism allows us to reexamine dissipative galaxy formation from a more general perspective. Stars are dynamical fossils; once some mass-fraction forms stars, dissipation effectively ceases for this component. Thus with care, we may hope to utilize the stellar characteristics of the oldest components of galaxies, the spheroids, as a tracer of their prior dissipative history.
There are strong indications that dissipation played an important
role in the formation of all galaxies, including the ellipticals and
dwarf spheroidals. The basic physical criterion in a dissipative model
is that the shocks driven by cloud collisions be radiative: if the
cloud surface density is too low or if the velocity too great,
resulting in inefficient cooling at high temperature, the compression
will be minimal. The star formation trigger requires radiative
cooling. Now the condition that a shock be radiative implies that the
column density of matter
 normal to
the plane of the shock must
exceed a critical value that depends only on the shock velocity
vsh
and temperature Ts of the newly-shocked
gas. Specifically, in a one-dimensional shock, we have
normal to
the plane of the shock must
exceed a critical value that depends only on the shock velocity
vsh
and temperature Ts of the newly-shocked
gas. Specifically, in a one-dimensional shock, we have
 crit
= n0 vsh
tcool(Ts), where
n0 is the preshock density, and
tcool is the post-shock cooling time. The
temperature itself Ts
crit
= n0 vsh
tcool(Ts), where
n0 is the preshock density, and
tcool is the post-shock cooling time. The
temperature itself Ts
 vsh2, and is inferred from the relative
cloud velocity. We
can therefore express the critical surface density for cooling in
terms of just one parameter, the cloud velocity dispersion, and we can
compare this relation with
vsh2, and is inferred from the relative
cloud velocity. We
can therefore express the critical surface density for cooling in
terms of just one parameter, the cloud velocity dispersion, and we can
compare this relation with
 and
and
 as measured for
spheroidal components of galaxies.
as measured for
spheroidal components of galaxies.
Earlier analyses described in Section 8.1 focused on the collapse of an initially uniform spherical cloud, for which the condition that the cooling time be less than the dynamical collapse time can be expressed as a locus in the density-temperature plane (Rees and Ostriker, 1977; Silk, 1977a). As we have seen, this suggested that the luminous extent of galaxies is indicative of the region where dissipation and star formation occurred. An extension of this scheme has attempted to understand the morphology of the Hubble sequence if the dissipative material collapses and forms stars in pre-existing dark halos (Faber, 1982). However, it is not the mean density but the local density, reflecting that of individual clumps of gas, that enters in determining whether stars form. It is likely that galaxy formation would result in extremely inhomogeneous and anisotropic initial conditions that could not be represented by uniform, spherically symmetric collapse.
A more general approach to dissipation is still possible that allows
confrontation with data. The stellar velocity dispersion
 provides a
fossilized measure of the cloud velocity dispersion at the epoch of
star formation and strong dissipation. The relation between
provides a
fossilized measure of the cloud velocity dispersion at the epoch of
star formation and strong dissipation. The relation between
 and
and
 is
therefore capable of providing us with a general framework for
studying the role of dissipation in collapsing inhomogeneous
star-forming clouds. The
is
therefore capable of providing us with a general framework for
studying the role of dissipation in collapsing inhomogeneous
star-forming clouds. The
 crit(
crit( ) relation is shown
in Figure 8.3 (taken from
Silk, 1983a)
for two alternative assumptions about cloud
compositions, corresponding to either primordial (including hydrogen
and 25% helium by mass) or solar abundances of heavy elements. The
primordial composition curve illustrates that H cooling by Lyman
) relation is shown
in Figure 8.3 (taken from
Silk, 1983a)
for two alternative assumptions about cloud
compositions, corresponding to either primordial (including hydrogen
and 25% helium by mass) or solar abundances of heavy elements. The
primordial composition curve illustrates that H cooling by Lyman
 excitation becomes ineffective below
excitation becomes ineffective below
 ~ 10 km
s-1, whereas heavy
elements provide fine-structure excitation degrees of freedom that
allow a finite value of
~ 10 km
s-1, whereas heavy
elements provide fine-structure excitation degrees of freedom that
allow a finite value of
 crit
even at low shock
velocities. The column
density evaluated for solar abundances scales approximately inversely
proportionately to the heavy element abundance, until the primordial
values of
crit
even at low shock
velocities. The column
density evaluated for solar abundances scales approximately inversely
proportionately to the heavy element abundance, until the primordial
values of
 crit
are attained. At shock velocities above
~ 103 km s-1, free-free cooling predominates.
crit
are attained. At shock velocities above
~ 103 km s-1, free-free cooling predominates.
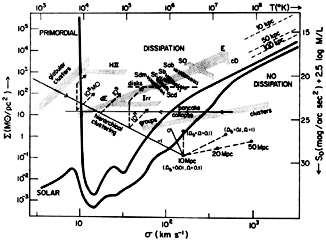 |
Figure 8.3. Dissipation diagram for galaxies
and clusters of galaxies. Surface density is in
M |
Now mean surface brightness and velocity dispersions can be measured or inferred for a wide variety of systems, including elliptical and spiral galaxies, dwarf galaxies, and galaxy groups and clusters. The mean surface brightness is defined as the blue luminosity of the spheroidal component, divided by the square of the half-light radius, and refers always to the stellar content of the system, since it is the matter now in stars that has undergone dissipation. This enables us to avoid a major uncertainty, namely the mass-to-luminosity ratio, since for the luminous components we know with reasonable accuracy what to take for this ratio, and can therefore readily compute the mean surface densities. Mean lines through the various observational correlations are displayed in Figure 8.3. Measurements of the maximum rotational velocities of discs generally probe the dynamics of the spheroidal components while core velocity dispersions are associated with the luminous stellar cores of ellipticals and SO's, and the surface densities refer to the luminous matter components. The velocity dispersions of galaxies in groups and clusters probe the dark matter distribution on megaparsec scales.
Some interesting conclusions can be drawn from inspection of Figure 8.3. Galaxies and globular clusters lie in the dissipative regime, whereas galaxy clusters and groups do not (see also Faber, 1982). Galaxy types are separated along the Hubble sequence in order of increasing degrees of surface density and of bulge velocity dispersion from late through early-type spirals to SO's and ellipticals. Indications of this separation have been noted before, but in any one-dimensional parameter space, there is considerable overlap in morphological type.
To explore the evolutionary significance of the
( ,
,
 ) diagram, we
consider the two rival schemes of hierarchical clustering and pancake
fragmentation for forming galaxies. As hierarchical clustering
proceeds, larger and larger mass-scales condense out of the expanding
universe. In the absence of dissipation, the mass-scale that first
becomes non-linear at epoch t increases as
t4/(n+3), where n
is the initial fluctuation spectral index. One infers that
) diagram, we
consider the two rival schemes of hierarchical clustering and pancake
fragmentation for forming galaxies. As hierarchical clustering
proceeds, larger and larger mass-scales condense out of the expanding
universe. In the absence of dissipation, the mass-scale that first
becomes non-linear at epoch t increases as
t4/(n+3), where n
is the initial fluctuation spectral index. One infers that
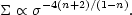 |
(8.25) |
This describes the relation of surface-density to velocity dispersion
for non-dissipative structure evolving from an initial power-law
fluctuation spectrum. Normalization is performed by comparison with
the galaxy distribution, for which the correlation function is unity
on a scale of
 5h-1 Mpc. The remaining uncertainty is to
decide what fraction the observed surface density at
5h-1 Mpc. The remaining uncertainty is to
decide what fraction the observed surface density at
 = 1 is of the
total (if
indeed the luminous matter is a satisfactory tracer); this uncertainty
similarly affects
= 1 is of the
total (if
indeed the luminous matter is a satisfactory tracer); this uncertainty
similarly affects  .
In Figure 8.3, we have therefore combined all
these unknown factors into the parameters
.
In Figure 8.3, we have therefore combined all
these unknown factors into the parameters
 b,
b,
 , and
n; for
appropriate choices, the hierarchical clustering theory describes a
unique line in the
(
, and
n; for
appropriate choices, the hierarchical clustering theory describes a
unique line in the
( ,
,
 ) plane. In
addition, there will be some
dispersion about any such line, since the phases of fluctuations are
unlikely to be random in the non-linear regime. Hierarchical
clustering evolution proceeds with increasing
) plane. In
addition, there will be some
dispersion about any such line, since the phases of fluctuations are
unlikely to be random in the non-linear regime. Hierarchical
clustering evolution proceeds with increasing
 , provided
n < 1, and towards increasing
, provided
n < 1, and towards increasing
 , provided
n > - 2.
, provided
n > - 2.
Next, we consider the one-dimensional collapse of an adiabatic pancake, for which
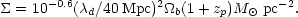 |
(8.26) |
As fragmentation occurs, one would expect the surface density of fragments to initially be comparable to the surface density of the initial pancake. Fragmentation should therefore proceed to smaller and smaller scales, until complex dissipative and dynamical processes produce more tightly bound structures.
Schematic evolution tracks for galaxy formation are also indicated. Suppose a group of fragments or clouds destined to be a galaxy evolves as a closed self-gravitating system. The locus of a constant mass track is
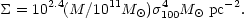 |
(8.27) |
Alternatively, suppose that an aggregate of gas clouds is
gravitationally bound by non-dissipative dark matter. Then as the gas
dissipates, it will maintain constant specific binding energy or
 = constant.
= constant.
Inspection of Figure 8.3 suggests that dwarf galaxies may be the crucial link between the initial fluctuations and luminous systems. Globular clusters are of high central surface brightness, and may also have formed in localized collapses at the same time as the galaxies. However, they have undergone considerable dynamical evolution, as indicated by their short core relaxation time-scales, and do not reveal any of the initial conditions relevant to formation of the galaxies. Another significant difference between globular clusters and ellipticals is inferred from abundance studies: globulars have a narrower intrinsic range in metallicity than do the dwarf spheroidals. This again is suggestive of a somewhat unique event that triggered their formation, rather than the slow chemical evolution that this theory associates with galaxies. It is the dwarf irregulars that bridge the gap between the emerging fluctuations and spirals, whereas dwarf spheroidals may be a transition between gas-rich systems and ellipticals.
While angular momentum has long been suspected to be the crucial
parameter that determines morphological type, it is seen here that the
dissipative history of a system may also play an important role. The
location of a galaxy in the
( ,
,
 ) plane is most directly
related to
Hubble type and is monitoring its past evolution and degree of
dissipation. Angular momentum is likely to limit dissipation for
rotationally supported systems, where tidal torques of dissipating gas
clouds in pre-existing dark halos can quantitatively account for the
observed specific angular momenta of discs
(Section 8.2).
) plane is most directly
related to
Hubble type and is monitoring its past evolution and degree of
dissipation. Angular momentum is likely to limit dissipation for
rotationally supported systems, where tidal torques of dissipating gas
clouds in pre-existing dark halos can quantitatively account for the
observed specific angular momenta of discs
(Section 8.2).
Mergers between protogalaxies in the initial stages of clustering (before large virial velocities have been acquired) may lead to SO and eventually to elliptical galaxy formation. After each merger, fewer and fewer clouds may be expected to survive that can potentially form a disc. Mergers between gas-rich systems may help to overcome some of the objections raised in Section 7.3, particularly the criticisms related to the high central velocity dispersions of ellipticals and metallicity gradients. These points are discussed in detail by Silk and Norman (1981).