


4.2.5. Velocity Dispersion Gradients
We have repeatedly seen how critically the dynamics of elliptical galaxies are affected by velocity anisotropies (see Binney 1981b, 1982a, b for reviews). These cannot be measured directly, because we observe only the projection of a velocity dispersion tensor which has many degrees of freedom. As a result, the interpretation of dispersion data is very model-dependent (Binney 1981b, 1982a; Illingworth 1981).
Observations of dispersion profiles in ellipticals are given in
Sargent et al. (1978),
Young et al. (1978a,
b),
Schechter and Gunn
(1978),
Jenkins and Scheuer
(1980),
Efstathiou, Ellis and Carter
(1980,
1982),
Davies (1981),
Davies et al. (1983),
and Fried and
Illingworth (1982).
Illingworth (1981)
reviews these data, and notes that two
general kinds of behavior are seen. Galaxies divide themselves
roughly equally into ones which have dispersions that decrease outward
(Fig. 35) and ones which have
 ~ constant (e.g.,
NGC 4697,
Fig. 36).
~ constant (e.g.,
NGC 4697,
Fig. 36).
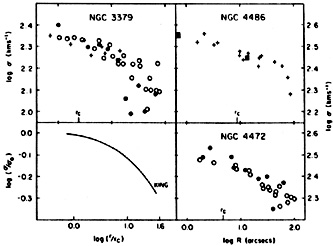 |
Figure 35. Velocity dispersion profiles in three elliptical galaxies and in a King (1966) model with constant M/L and log(rt / rc) = 2.25 (from Illingworth 1981, who also gives the data sources). |
Many of the falling dispersion profiles are consistent with King (1966) models that have isotropic residuals and constant M/L (see Fig. 35). Such models also give reasonably good fits to the photometry (King 1978; Kormendy 1977c). Thus some ellipticals may be isotropic with constant M/L to radii r ~ 10 - 50rc. If galaxies like NGC 4697 are also isotropic, then M/L must increase with radius, as it does in spirals. However, there are many reasons for believing that ellipticals are not generally isotropic, especially outside their cores. For example, dissipationless galaxy formation leads to velocity ellipsoids which tend to be more and more radially elongated at larger radii. This is also the behavior of realistic models (e.g., Schwarzschild 1979, see Merritt 1980; Wilkinson and James 1982). Furthermore, anisotropy is also implied by the photometric (section 3.3.1) and kinematic (section 4.2.6) evidence that ellipticals are triaxial. Finally, the Galactic bulge locally has a larger radial than azimuthal dispersion (Oort 1965; Delhaye 1965; Woolley 1978). If ellipticals have larger radial than azimuthal dispersions, then even galaxies with falling dispersion profiles can have M/L values which increase with radius. Dispersion profiles provide very little constraint on the mass distribution; there is too much freedom to trade mass for velocity anisotropy (Binney 1981b, 1982a).
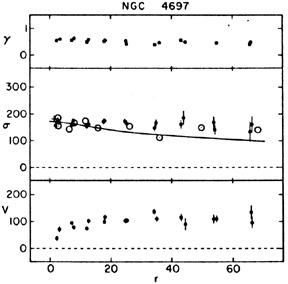 |
Figure 36. Rotation velocity V (km
s-1), velocity dispersion
|
If the mass distribution is as strongly peaked toward the center
as in an r1/4 law, then typical models discussed by
Binney (1980b)
have dispersions which reach a maximum at
r/re ~ 0.05 - 0.2 (depending
on the amount of anisotropy), and then decrease at the center to
 40%
of the maximum value. For the three ellipticals in
Figure 35, the above radius range is
1.2" - 5.0" in NGC 3379, 3.4" - 14" in M87 and
6" - 23" in NGC 4472 (re from
Kormendy 1977c).
Thus a central decrease
in
40%
of the maximum value. For the three ellipticals in
Figure 35, the above radius range is
1.2" - 5.0" in NGC 3379, 3.4" - 14" in M87 and
6" - 23" in NGC 4472 (re from
Kormendy 1977c).
Thus a central decrease
in  could be masked by
seeing in NGC 3379 but probably not in M87 or
NGC 4472. No such decrease is seen. This is
consistent with the fact
that the latter galaxies have clearly resolved cores
(section 3.3.8). The
small dispersion gradient at
r < rc in M87 was discussed in
section 3.3.8; it
could imply a radial variation in either M/L or the anisotropy.
could be masked by
seeing in NGC 3379 but probably not in M87 or
NGC 4472. No such decrease is seen. This is
consistent with the fact
that the latter galaxies have clearly resolved cores
(section 3.3.8). The
small dispersion gradient at
r < rc in M87 was discussed in
section 3.3.8; it
could imply a radial variation in either M/L or the anisotropy.
A nuclear dispersion minimum has been detected in only one elliptical.
Efstathiou, Ellis and
Carter (1982)
report that velocity
dispersions in the E2-3 galaxy NGC 5813 peak at 230 ± 8 km
s-1 at r ~ 12" and then decrease to ~ 200 km
s-1 at the center. This effect
is detectable partly because the core is so large,
rc ~ 14" (seeing
 *
*
 0.6").
Efstathiou and collaborators conclude that the galaxy is
isotropic near the center, but has
0.6").
Efstathiou and collaborators conclude that the galaxy is
isotropic near the center, but has
 r ~
1.6
r ~
1.6
 ~
1.6
~
1.6
 at large
radii (
at large
radii ( r,
r,

 ,
,

 are the
radial and tangential components of the dispersion, respectively). Out to
r ~ 6.5rc, M/L increases by a
factor of ~ 2. It is interesting to note that NGC 5813 is peculiar in several ways. Its
core radius rc ~ 2.5 kpc (H0 = 50 km
s-1 Mpc-1) is very large for a
galaxy with MB = -21.5 (see
Figs. 33 and
22). Also, the rotation
curve has a large peak at small radii: V ~ 89 ± 7 km
s-1 at
r
are the
radial and tangential components of the dispersion, respectively). Out to
r ~ 6.5rc, M/L increases by a
factor of ~ 2. It is interesting to note that NGC 5813 is peculiar in several ways. Its
core radius rc ~ 2.5 kpc (H0 = 50 km
s-1 Mpc-1) is very large for a
galaxy with MB = -21.5 (see
Figs. 33 and
22). Also, the rotation
curve has a large peak at small radii: V ~ 89 ± 7 km
s-1 at
r  3.2",
but V ~ 8 ± 2 km s-1 for
10"
3.2",
but V ~ 8 ± 2 km s-1 for
10"  r
r
 80"; contrast the
normal rotation curve of NGC 4697 (Fig. 36).
Finally, the brightness profile appears
to deviate above an isothermal core at the center. These peculiarities
recall a question that I asked at the end of
section 3.3.8. Would an object
like NGC 5813 result if a giant elliptical merged with a
less massive
one which had a smaller central velocity dispersion (the Faber-Jackson
relation), a smaller core radius
(Fig. 22), a higher central
surface brightness (I0
80"; contrast the
normal rotation curve of NGC 4697 (Fig. 36).
Finally, the brightness profile appears
to deviate above an isothermal core at the center. These peculiarities
recall a question that I asked at the end of
section 3.3.8. Would an object
like NGC 5813 result if a giant elliptical merged with a
less massive
one which had a smaller central velocity dispersion (the Faber-Jackson
relation), a smaller core radius
(Fig. 22), a higher central
surface brightness (I0
 rc-0.87, see
section 4.2.3) and more rapid rotation
(Davies et al. 1983)?
rc-0.87, see
section 4.2.3) and more rapid rotation
(Davies et al. 1983)?