


5.7.3. Thermal instability and optical filamentation
As the gas cools, any inhomogeneities in the gas density will tend to be
amplified
(Fabian and Nulsen,
1977).
In a region of higher than average density, the
temperature will tend to be lower, to preserve pressure
equilibrium. Both higher
density and lower temperature will speed up the cooling rate, and
lowering the temperature will increase the density contrast.
Mathews and Bregman
(1978)
analyzed the growth of density inhomogeneities and the thermal
instability of the
cooling gas. They considered only radial comoving, isobaric
perturbations (no
change in the velocity or pressure as compared to the unperturbed flow
at the same position), and assumed
 is constant. They
found that the gas is thermally unstable if
is constant. They
found that the gas is thermally unstable if
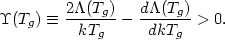
| (5.108) |
This is true for any interesting gas temperature (Tg
 105
K). Assuming that there is an initial perturbation of relative amplitude
(
105
K). Assuming that there is an initial perturbation of relative amplitude
(
 /
/
 )i at
some large radius ri, the amplified perturbation at an
inner radius r < ri is
)i at
some large radius ri, the amplified perturbation at an
inner radius r < ri is
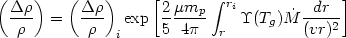
| (5.109) |
in the linear regime
((
 /
/
 ) <<
1). Mathews and Bregman found that
amplification factors of 103-4 were likely for flows into the
sonic radius.
White and Sarazin
(1987a)
generalized the perturbation analysis to arbitrary
perturbations and flows with sinks for gas
(
) <<
1). Mathews and Bregman found that
amplification factors of 103-4 were likely for flows into the
sonic radius.
White and Sarazin
(1987a)
generalized the perturbation analysis to arbitrary
perturbations and flows with sinks for gas
(
 const), and showed that
the flow is always unstable if inequality 5.108 is satisfied, and that the
fastest growing mode is radial, comoving, and isobaric, and is amplified
according to equation 5.109. Thermal conduction could suppress the thermal
instability of cooling flows, unless conduction is itself suppressed by
magnetic fields.
const), and showed that
the flow is always unstable if inequality 5.108 is satisfied, and that the
fastest growing mode is radial, comoving, and isobaric, and is amplified
according to equation 5.109. Thermal conduction could suppress the thermal
instability of cooling flows, unless conduction is itself suppressed by
magnetic fields.
Cowie et al.
(1980)
generalized this analysis by considering the motion of
finite sized 'blobs' with a finite density perturbation, without
assuming that the blobs comove with the flow. They argue that the motion
of blobs relative to the unperturbed gas (bouyancy) will stabilize some
perturbations, but that the gas
will still be unstable for some blob sizes and densities. Because they
assume the flow stagnates, the inflow must become very unstable for
r  rst.
rst.
Given that the gas in cooling flows is thermally unstable and that the growth time for the instability is comparable (or somewhat shorter than) the cooling time, these flows should become very inhomogeneous unless the inflowing intracluster gas were very smooth. Thus it may not be reasonable to model the flows with a single phase; multiphase models for cooling flows are discussed in Section 5.7.5.
Optical emission line filaments are often seen near the centers of clusters
having cooling flows, often within the central galaxies that are
accreting the cooling gas
(Ford and Butcher, 1979;
Kent and Sargent, 1979;
Stauffer and Spinrad,
1979;
Heckman, 1981;
Fabian et al.,
1981b,
1982a;
Cowie et al.,
1983;
Hu et al., 1983,
1985;
van Breugel et
al., 1984).
The size of these extended
filament systems ranges roughly from 1-100 kpc. These filaments emit the
Balmer lines of hydrogen, as well as forbidden lines from heavier
elements. Their spectra are similar to those seen in astrophysical
shocks. The emission from these filaments is generally believed to be
the result of the same cooling flows; the gas
is visible in optical line emission as it cools through the temperature
range Tg
 104 K. The
clumpy nature of these filaments is due, at least in part, to
thermal instability in the cooling gas as discussed above.
Figure 20
shows the optical filaments around NGC1275 in the Perseus cluster, which is one of
the best studied examples of this optical filamentation
(Lynds, 1970).
Clusters with cooling flows having optical filamentation are listed in
Table 4.
104 K. The
clumpy nature of these filaments is due, at least in part, to
thermal instability in the cooling gas as discussed above.
Figure 20
shows the optical filaments around NGC1275 in the Perseus cluster, which is one of
the best studied examples of this optical filamentation
(Lynds, 1970).
Clusters with cooling flows having optical filamentation are listed in
Table 4.
Cowie et al. (1980,
1983)
have derived the total luminosity in the
H line
expected in a cooling flow; they find
line
expected in a cooling flow; they find
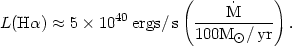
| (5.110) |
This is somewhat larger than would be derived from equation (5.102), which
assumes isobaric cooling. Thermally unstable blobs of gas probably cool
nearly isobarically until Tg
 106 K; at
lower temperatures the cooling time is shorter
than the sound crossing time for the filaments, and the gas initially cools
isochorically (at constant density). The cool clumps reach pressure
equilibrium
with the surrounding hot gas by the passage of repressurizing shocks
(Mathews and Bregman,
1978;
Cowie et al.,
1980).
The H
106 K; at
lower temperatures the cooling time is shorter
than the sound crossing time for the filaments, and the gas initially cools
isochorically (at constant density). The cool clumps reach pressure
equilibrium
with the surrounding hot gas by the passage of repressurizing shocks
(Mathews and Bregman,
1978;
Cowie et al.,
1980).
The H flux may
also be increased by photoionization by X-rays and ultraviolet radiation
from the surrounding hot gas or from the nuclear source in the accreting
galaxy.
flux may
also be increased by photoionization by X-rays and ultraviolet radiation
from the surrounding hot gas or from the nuclear source in the accreting
galaxy.
Cowie et al. (1983) have suggested, based on extensive observations of optical line emission, that these filament systems consist of two components: a cluster core component, which is 20-100 kpc in size, and a galaxy component, which is smaller. In some clusters both components are present; in some, only one or the other is observed. The larger cluster components tend to consist of highly elongated filaments, which may be stretched by tidal effects in the cluster or along the magnetic field lines. The galaxy components are more homogeneous, and are also elongated. Cowie et al. suggest that they are gas disks at the stagnation radius. In many clusters the filament systems show velocity shears consistent with centrifugally supported disks (Hu et al., 1985), although velocity measurements in NGC1275 indicate that the gas is not rotating fast enough in this galaxy (Hu et al., 1983). These emission line gas disks can be used to estimate the masses of the inner portions of the cD galaxies, just as the rotation velocities of spiral galaxy disks are used to determine their masses (Hu et al., 1985).
Hu et al. (1985)
find that the presence of optical emission line filaments in the
central galaxies of clusters correlates very strongly with the central
density of the
intracluster gas. The emission lines are only found in clusters with
central proton number densities n0
 5 ×
10-3 h501/2
cm-3. This is just what is expected if
the emission lines are due to cooling flows, since a lower limit on the
density implies an upper limit on the cooling time. For this density limit
and an intracluster gas temperature of 7 × 107 K,
equation (5.23) gives tcool
5 ×
10-3 h501/2
cm-3. This is just what is expected if
the emission lines are due to cooling flows, since a lower limit on the
density implies an upper limit on the cooling time. For this density limit
and an intracluster gas temperature of 7 × 107 K,
equation (5.23) gives tcool
 1010
h50 - 1/2 yr, which implies that the gas
could cool in the lifetime of the cluster.
1010
h50 - 1/2 yr, which implies that the gas
could cool in the lifetime of the cluster.
The filament system around NGC1275 in the Perseus cluster is the most luminous such system known, and is considerably brighter than would be expected given the accretion rate determined from the X-ray measurements. Hu et al. (1983) argue that it is also too luminous to be due to photoionization by the nuclear source in NGC1275. They show that the optical filaments at the velocity of NGC1275 are elongated at the same position and in the same direction as the filaments due to the spiral galaxy that is moving towards NGC1275 at 3000 km/s (see Section 4.5.2). They suggest that this galaxy is actually colliding with the base of the accretion flow onto NGC1275, and that the kinetic energy in this collision powers the emission line filaments. Two problems with this model, which are discussed by Hu et al., are the lack of intermediate velocity gas and the difficulty of a gas-rich galaxy penetrating into the core of the Perseus cluster without having its gas stripped (Sections 2.10.2 and 5.9).