5.7.2. Accretion by central galaxies

Many clusters of galaxies have luminous galaxies located at their centers (Section 2.10.1), and these galaxies appear to be moving relatively slowly compared to the average cluster galaxy (Quintana and Lawrie, 1982). In fact, such a luminous galaxy is found at the center of every cooling flow that has been observed (Jones and Forman, 1984). The cooling intracluster gas may, then, be accreted by the central galaxy in the cluster when its temperature has fallen to the point where it can be bound to the galaxy, and the gas can cool further and flow into the galaxy center (Silk, 1976; Cowie and Binney, 1977; Fabian and Nulsen, 1977; Mathews and Bregman, 1978).

It is unlikely that the presence of the central galaxy causes the cooling flow (that is, increases the cooling rate significantly) because the gravitational potential associated with a galaxy is much smaller than that associated with a cluster (cluster velocity dispersions are much larger than those of galaxies). Thus the presence of a central galaxy will not cause a large perturbation in the density of hydrostatic intracluster gas (Section 5.5) and will not affect the cooling rate significantly. Initially, the inflow of cooling gas is driven by the pressure of the surrounding hot medium; only when the gas has cooled significantly does the gravitational potential of the galaxy influence the flow. If the mass of the central galaxy is small, the flow may be pressure-driven over most of its extent (Fabian and Nulsen, 1977; Binney and Cowie, 1981).

In order to accrete cooling gas, a galaxy must be moving slowly through the intracluster medium. The gas must be able to cool before the galaxy has moved away. Thus the velocity is limited to

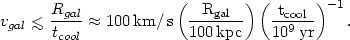
(5.103)

Thus a typical cluster galaxy with v_{gal r} 10³ km/s will have great difficulty accreting. Central dominant galaxies are expected to have velocities of at least 100 km/s on average, due to gravitational encounters with other galaxies (Section 2.9.1). Based on the asymmetry in the nonthermal radio emission and optical line filaments around the galaxy M87 in the Virgo cluster, De Young et al. (1980) argued that this accreting galaxy was moving about 200 km/s to the north. Dones and White (1985) showed that this was inconsistent with the observed temperature structure in the cooling flow; that is, it would strongly violate this cooling limit.

Models for the accretion of cooling gas onto central galaxies have been given by Fabian and Nulsen (1977), Mathews and Bregman (1978), and Binney and Cowie (1981). All of these calculations assume the = 0 in equations (5.101); the sources of the gas are external to the central galaxy, so that is constant within the galaxy. Mathews and Bregman integrate equations (5.101) inward through a sonic radius r_s at which the inflow becomes supersonic. The structure of the flow is determined by and the gas temperature at the sonic radius T_s. The sonic radius is a solution of the following equation (Mathews and Bregman, 1978):

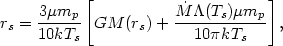
(5.104)

where M(r) is the total galactic and cluster mass within the radius r. This equation can have multiple solutions, although usually only one of these at most corresponds to an astrophysically interesting density. For reasonable values of and T_s, one finds r_s 0.1 - 2 kpc (Mathews and Bregman, 1978). A simple estimate of the sonic radius can be derived in a number of ways. First, if the inflow is driven by cooling rather than gravity, then the second term in equation (5.104) will be more important. This is essentially equivalent to arguing that the inflow time and cooling time must be roughly equal. Second, even if gravity is important to the inflow, kT_g / µ m_p GM(r) / r (see discussion after equations 5.101), and the first term in equation (5.104) only increases r_s by several times. Thus an estimate for r_s is

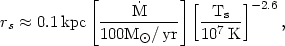
(5.105)

where the cooling function in equation (5.22) has been used. Note that r_s is proportional to .

On the other hand, Fabian and Nulsen (1977) and Cowie et al. (1980) argued that the gas cannot flow in as far as r_s because the inflowing gas must have at least a small amount of angular momentum. Let l r × v be the angular momentum per unit mass of the incoming gas, and assume that this is conserved. Then the inflow will stop and the gas will form a rotating disk at a stagnation radius r_st given by

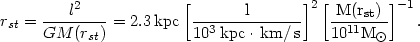
(5.106)

Ideally, the angular momentum of inflowing gas in a spherical cluster would be zero, but realistically the gas must have some nonradial velocity. Cowie et al. argued that the gas was ejected by cluster galaxies, and that the angular momentum of the central cooling gas would be determined by the rms residual velocity of galaxies in the cluster core,

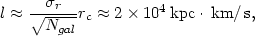
(5.107)

where _r is the cluster velocity dispersion, N_gal 100 is the number of galaxies in the cluster core, and r_c is the cluster core radius. Alternatively, if the gas had no nonradial motion relative to the cluster, l might be due to the central galaxy orbital velocity, which for v_gal 100 km/s and a galaxy orbital radius of 30 kpc gives l 3 × 10³ kpc ^. km/s. However, both of these estimates imply gas velocities relative to the central galaxy that exceed the cooling time scale limit (equation 5.103). Taking this limit at a cooling radius of 200 kpc gives l 4 × 10³ kpc ^. km/s. Thus, unless the inflow is much more radial than these estimates suggest, it is likely that the flow will stagnate before becoming supersonic (r_st r_s).

Viscosity (Section 5.4.4) might transport angular momentum out of the flow and reduce l. If ionic viscosity is effective, thermal conduction will probably also be important and may suppress the cooling flow (Cowie et al., 1980). However, the magnetic field may couple the inner and outer parts of the flow and provide an effective viscosity; a circumferential field could both transport angular momentum out of the inflow, and suppress thermal conduction. Alternatively, if the magnetic field were too weak to be dynamically important and the ionic viscosity were small, the Reynolds number for the flow would be large and the flow could become turbulent. Turbulent viscosity might transport angular momentum out of the flow (Nulsen et al., 1984), and, at the same time, the turbulence could tangle the magnetic field and inhibit thermal conduction.

Cowie et al. (1980) treated the inflow as radial (which is reasonable for r >> r_st), and included the effect of angular momentum by adding a repulsive centrifugal potential _cent = l² / 2r² to the gravitational potential in equations (5.101). Moreover, they assumed that r_st >> r_s, and therefore they dropped all quadratic or higher order terms in the flow velocity v.

If the accretion rate in the flow decreases inward (d / dr > 0), the radial flow can continue into the center of the galaxy without passing through a sonic radius (Nulsen et al., 1984). There is some evidence that does decrease inwards in M87/Virgo and NGC1275/Perseus (Fabian et al., 1984b; Stewart et al., 1984a). It may be that some of the cooling gas is being converted into stars (Section 5.7.4 below).

Many central galaxies in clusters with cooling flows have nuclear nonthermal radio sources, which may be powered by the further accretion of a small portion of the cooling gas onto the central 'engines' (black holes?) of these sources (Burns et al., 1981b; Bijleveld and Valentijn, 1983; Valentijn and Bijleveld, 1983; Jones and Forman, 1984; Nulsen et al., 1984). There is evidence for a correlation between the radio luminosity and accretion rate in these galaxies (Valentijn and Bijleveld, 1983; Jones and Forman, 1984).