Annu. Rev. Astron. Astrophys. 1994. 32: 319-70 Copyright © 1994 by . All rights reserved

1. INTRODUCTION

In 1964, Penzias & Wilson (1965) serendipitously detected the microwave background as anomalous excess noise, coming from all directions and corresponding to a temperature of ~ 3 K. This was immediately interpreted as being a relic of the Primeval Fireball by Dicke et al (1965), who had already been preparing an experiment in the hope of detecting it. Recently the remarkable success of the FIRAS instrument on the COBE satellite has confirmed that the cosmic microwave background radiation has a Planck spectrum with (Mather et al. 1994)

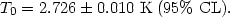
(1)

The blackbody nature of the cosmic microwave background (CMB) strongly suggests an origin in the early universe. In the standard Big Bang model thermalization occurred at an epoch t 1 yr or T 10⁷ K. By 1975, the remote origin of the CMB was supported by the high degree of isotropy apart from the detection of the dipole anisotropy (Corey & Wilkinson 1976, Smoot et al 1977). The best-fitting dipole is D_obs = 3.343 ± 0.016 mK (95% CL) towards (, b) = (264.°4 ± 0.3, 48.°4 ± 0.°5) (Smoot et al 1991, 1992; Kogut et al 1993; Fixsen et al 1994). After correction for the motion of the Earth around the Sun, the Sun around the Galaxy, and the Galaxy relative to the center of mass of the Local Group, one infers (Smoot et al 1991, Kogut et al 1993) that our Local Group of galaxies is moving at a velocity of 627 ± 22 km s^-1 in a direction (, b) = (276° ± 3°, 30° ± 3°). Convergence of the local velocity vectors to the CMB dipole does not occur until a distance of > 100h^-1 Mpc (herein the Hubble constant H₀ = 100h km s^-1 Mpc^-1), according to the dipole measured in the IRAS all-sky galaxy redshift survey (Strauss et at 1992), and possibly to > 150h^-1 Mpc if the recent claim of a dipole in the nearby Abell cluster frame is confirmed (Lauer & Postman 1992, 1993; see also Plionis & Valdarnini 1991). Theoretical arguments actually suggest that convergence may only be logarithmic (Juszkiewicz et al 1990) if the large-scale density fluctuation spectrum has the Harrison-Zel'dovich form, / ^-(n+3)/2 with n = 1 (Harrison 1970, Peebles & Yu 1970, Zel'dovich 1972).

Detection of anisotropy on smaller scales than that of the dipole has proved extremely difficult. The original detection paper set limits of about 10% on any anisotropy (Penzias & Wilson 1965). By 1968, the first simplistic theoretical prediction; suggested that galaxy formation implied fluctuations in the CMB of the order of 1 part in 10² (Sachs & Wolfe 1967) or 10³ (Silk 1967, 1968). As experimental sensitivity improved, the theoretical calculations grew more sophisticated (e.g. Peebles & Yu 1970, Doroshkevich et al 1978, Wilson & Silk 1981), predicting T / T ~ 10^-4 for universes containing predominantly baryonic matter. Claims of an electron neutrino mass of about 30eV (Lyubimov et al 1980) stimulated interest in non-baryonic dark matter-dominated universes (e.g. Bond et al 1980, Doroshkevich et al 1980). Neutrinos as dark matter failed to account for structure formation (e.g. Kaiser 1983; White et al 1983, 1984) despite the fact that the neutrino window (now closed for _e but still open for _µ or ) allows neutrinos to be a plausible dark matter candidate (e.g. Steigman 1993).

After 1980, the inflationary cosmology (see Narlikar & Padmanabhan 1991 for a review) revived interest in non-baryonic dark matter, now considered more likely to be of the cold variety (e.g. Peebles 1982a, Blumenthal et at 1984, Frenk et al 1990). The hot/cold classification (Bond & Szalay 1983) amounts to the velocity dispersion of the candidate particle being much greater or much less than the canonical escape velocity of a typical galaxy: ~ 300 km s^-1 at the epoch of equal densities of matter and radiation, 1 + z_eq = 23,900(₀ h²). Only at later times does substantial sub-horizon fluctuation growth occur.

As limits improved on small-scale fluctuations, to T / T ~ 10^-4 (Uson & Wilkinson 1984a, b, c), refined theoretical estimates showed that, with the aid of dark matter, one could further reduce T / T by an order of magnitude. (For a summary of the pre-COBE experimental situation see Partridge 1988, Readhead & Lawrence 1992). The experimental breakthrough came in 1992 (Smoot et al 1992) with the first detection of large angular scale anisotropies of cosmological origin in the CMB by the COBE DMR experiment (Smoot et al 1990). This has since been confirmed by at least one other experiment (Ganga et al 1993). Because of the sky coverage and frequency range spanned, one can now, with confidence, eliminate any Galactic explanation, as well as the possibility that nearby superclusters containing diffuse hot gas are imprinting Sunyaev-Zel'dovich fluctuations on the CMB (Hogan 1992; Rephaeli 1993a, b; Bennett et al 1993). This conclusion is further strengthened by the lack of correlation with the X-ray background (Boughn & Jahoda 1993). Fluctuations are telling us about density perturbations at z ~ 1000. The first year DMR data represent a > 7 detection; the best determined measurement is the sky variance on scales of 10°, _obs(10°) = 30 ± 5µK (Smoot et al 1992).

Several other experiments have subsequently reported detections on intermediate angular scales, ~ 1° (with nine separate claims of detection of fluctuations by the end of 1993). These are all generally consistent with the COBE amplitude, given plausible extrapolation from the large angular scales, as described below, although there is cause for serious concern about foreground Galactic contamination as a consequence of limited sky and frequency coverage.

We are certainly now on the verge of a quantum leap in cosmological modeling. Large-scale "seed" power has been discovered at a level of T / T ~ 10^-5. These fluctuations are the fossil precursors of the largest structures we see today, which have scales of 50h^-1 Mpc. On angular scales 10°, they are also relics of the apparently noncausal initial conditions in the Big Bang, which can be accounted for by inflationary cosmology, and hence provide a possible verification of inflation. Gravity waves are another legacy from inflation, and can leave a distinguishable signature imprinted on the CMB [see Burke (1975) and Doroshkevich et al (1977) for a pre-inflation view]. Indeed, there have been recent proposals to utilize the CMB fluctuations on large scales to reconstruct the inflaton potential.

The connection between large-scale power in the matter distribution and that in the CMB is conceptually simple, if at early epochs one is in the linear regime. At large redshift, a comoving scale of 100 Mpc projects to an angular scale of approximately ₀ h degrees. Complications arise for several reasons. First, the statistical properties of the fluctuations are not known a priori. Inflation predicts that the fluctuations are Gaussian. However, in non-inflationary cosmologies, especially likely if ₀ < 1 as favored by observations of the local universe, the initial conditions are non-Gaussian. Moreover, one may have non-linear topological defects as the source of seed density fluctuations. We cannot yet predict with much confidence the likely implications of such models for CMB anisotropies, largely because the connection with large-scale structure observations, to which the theory must ultimately be normalized, is tenuous.

Given an initial spectrum of density fluctuations, (k), one can calculate the transfer function to obtain the radiation power spectrum P_rad(k). The scale z_eq ( h²) is imprinted, thereby inevitably guaranteeing a dependence proportional both to ₀ and, when normalized to an observed scale, to H₀. Curvature can complicate the matter further since, in a low ₀ universe, on scales larger than the curvature radius there is no unique definition of the matter fluctuation power spectrum.

Other cosmological model parameters that enter less directly are _B, and , the contributions to ₀ in baryons, vacuum, and massive neutrinos, respectively. These all modify the detailed transfer function for a given (k). The ionization history of the Universe is yet another unknown. The intergalactic medium is highly ionized at z = 5. If it were even 90% ionized at z 20, the modification of the predicted T / T can become significant, at the 10-20% level, on angular scales of a few degrees. If ionization occurred much earlier, there is strong smoothing of degree-scale fluctuations, but at the cost of regenerating them, together with subarcminute-scale fluctuations in second order, on the new last scattering surface.

This review is arranged as follows. Section 1 presents an overview of recombination, and introduces the various sources of temperature fluctuations. Section 2 summarizes structure formation theory, and the different fluctuation modes. The power spectrum formalism is described in Section 3. In Section 4, we review Gaussian autocorrelation function fitting, window functions, and alternative approaches to data analysis. Higher order effects (such as reionization) are described in Section 5. Problems arising from various types of uncertainties are summarized in Section 6. Section 7 discusses alternatives to the "standard" model and Section 8 describes some issues that a new generation of experiments will have to address.