B.5.4. Results: The Hubble Constant and Dark Matter

With our understanding of the theory and observations of the lenses we will now explore their implications for H₀. We focus on the "simple" lenses PG1115+080, SBS1520+530, B1600+434, and HE2149-2745. We only comment on the interpretation of the HE1104-1805 delay because the measurement is too recent to have been interpreted carefully. We will briefly discuss the more complicated systems B0218+357, RXJ0911+0551, Q0957+561, and B1608+656, and we will not discuss the systems with problematic time delays or astrometry.

The most common, simple, realistic model of a lens consists of a singular isothermal ellipsoid (SIE) in an external (tidal) shear field (see Section B.4). The model has 7 parameters (the lens position, mass, ellipticity, major axis orientation for the SIE, and the shear amplitude and orientation). It has many degrees of freedom associated with the angular structure of the potential, but the radial structure is fixed with <> 1/2. For comparison, a two-image (four-image) lens supplies 5 (13) constraints on any model of the potential: 2 (6) from the relative positions of the images, 1 (3) from the flux ratios of the images, 0 (2) from the inter-image time delay ratios, and 2 from the lens position. With the addition of extra components (satellites/clusters) for the more complex lenses, this basic model provides a good fit to all the time delay lenses except Q0957+561. Although a naive counting of the degrees of freedom (N_dof = - 2 and 6, respectively) suggests that estimates of H₀ would be under constrained for two-image lenses and over constrained for four-image lenses, the uncertainties are actually dominated by those of the time delay measurements and the astrometry in both cases. This is what we expect from Section B.5.1 - the model has no degrees of freedom that change <> or , so there will be little contribution to the uncertainties in H₀ from the model for the potential.

If we use a model that includes parameters to control the radial density profile (i.e., <>), for example by adding a halo truncation radius a to the SIS profile [the pseudo-Jaffe model, r^-2(r² + a²)^-1; e.g., Impey et al. 1998; Burud et al. 2002a], ⁵ then we find the expected correlation between a and H₀ - as we make the halo more concentrated (smaller a), the estimate of H₀ rises from the value for the SIS profile (<> = 1/2 as a ) to the value for a point mass (<> = 0 as a 0), with the fastest changes occurring when a is similar to the Einstein radius of the lens. We show an example of such a model for PG1115+080 in Figure B.36. This case is somewhat more complicated than a pure pseudo-Jaffe model because there is an additional contribution to the surface density from the group to which the lens galaxy belongs. As long as the structure of the radial density profile is fixed (constant a), the uncertainties are again dominated by the uncertainties in the time delay. Unfortunately, the goodness of fit, ²(a), shows too little dependence on a to determine H₀ uniquely. In general, two-image lenses have too few constraints, and the extra constraints supplied by a four-image lens constrain the angular structure rather than the radial structure of the potential. This basic problem holds for all existing models of the current sample of time delay lenses.

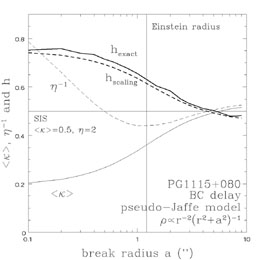Figure B.36. H0 estimates for PG1115+080. The lens galaxy is modeled as an ellipsoidal pseudo-Jaffe model, r-2(r2 + a2)-1, and the nearby group is modeled as an SIS. As the break radius a the pseudo-Jaffe model becomes an SIS model, and as the break radius a 0 it becomes a point mass. The heavy solid curve (hexact) shows the dependence of H0 on the break radius for the exact, nonlinear fits of the model to the PG1115+080 data. The heavy dashed curve (hscaling) is the value found using our simple theory (Section B.5.1) of time delays. The agreement of the exact and scaling solutions is typical. The light solid line shows the average surface density <> in the annulus between the images, and the light dashed line shows the inverse of the logarithmic slope in the annulus ( 1 - ). For an SIS model we would have <> = 1/2 and -1 = 1/2, as shown by the horizontal line. When the break radius is large compared to the Einstein radius (indicated by the vertical line), the surface density is slightly higher and the slope is slightly shallower than for the SIS model because of the added surface density from the group. As we make the lens galaxy more compact by reducing the break radius, the surface density decreases and the slope becomes steeper, leading to a rise in H0. As the galaxy becomes very compact, the surface density near the Einstein ring is dominated by the group rather than the galaxy, so the surface density approaches a constant and the logarithmic slope approaches the value corresponding to a constant density sheet ( = 1).

The inability of the present time delay lenses to directly constrain the radial density profile is the major problem for using them to determine H₀. Fortunately, it is a consequence of the available data on the current sample rather than a fundamental limitation. It is, however, a simple trade-off - models with less dark matter (lower <>, more centrally concentrated densities) produce higher Hubble constants than those with more dark matter. We do have some theoretical limits on the value of <>. In particular, we can be confident that the surface density is bounded by two limiting models. The mass distribution should not be more compact than the luminosity distribution, so a constant mass-to-light ratio (M / L) model should set a lower limit on <> <>_M/L 0.2, and an upper limit on estimates of H₀. We are also confident that the typical lens should not have a rising rotation curve at 1-2 optical effective radii from the center of the lens galaxy. Thus, the SIS model is probably the least concentrated reasonable model, setting an upper bound on <> <>_SIS = 1/2, and a lower limit on estimates of H₀. Figure B.37 shows joint estimates of H₀ from the four simple lenses for these two limiting mass distributions (Kochanek 2003b). The results for the individual lenses are mutually consistent and are unchanged by the new 0.149 ± 0.004 day delay for the A₁-A₂ images in PG1115+080 (Chartas [2003]). For galaxies with isothermal profiles we find H₀ = 48 ± 3 km s^-1 Mpc^-1, and for galaxies with constant M / L we find H₀ = 71 ± 3 km s^-1 Mpc^-1. While our best prior estimate for the mass distribution is the isothermal profile (see Section B.4.6), the lens galaxies would have to have constant M / L to match Key Project estimate of H₀ = 72 ± 8 km s^-1 Mpc^-1 (Freedman et al. [2001]) or the WMAP estimate of H₀ = 72 ± 5 km s^-1 Mpc^-1 for a flat universe with a cosmological constant (Spergel et al. [2003]).

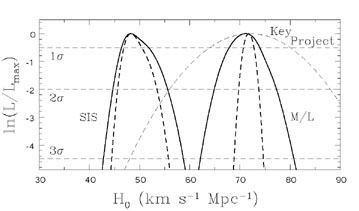Figure B.37. H0 likelihood distributions. The curves show the joint likelihood functions for H0 using the four simple lenses PG1115+080, SBS1520+530, B1600+434, and HE2149-2745 and assuming either an SIS model (high <>, flat rotation curve) or a constant M / L model (low <>, declining rotation curve). The heavy dashed curves show the consequence of including the X-ray time delay for PG1115+080 from Chartas (2003) in the models. The light dashed curve shows a Gaussian model for the Key Project result that H0 = 72 ± 8 km s-1 Mpc-1.

The difference between these two limits is entirely explained by the differences in <> and between the SIS and constant M / L models. In fact, it is possible to reduce the H₀ estimates for each simple lens to an approximation formula, H₀ = A(1 - <>) + B<>( - 1). The coefficients, A and | B| A / 10, are derived from the image positions and the time delay using the simple theory from Section B.5.1. These approximations reproduce numerical results using ellipsoidal lens models to accuracies of 3 km s^-1 Mpc^-1 (Kochanek [2002a]). For example, in Figure B.36 we also show the estimate of H₀ computed based on the simple theory of Section B.5.1 and the annular surface density (<>) and slope () of the numerical models. The agreement with the full numerical solutions is excellent, even though the numerical models include both the ellipsoidal lens galaxy and a group. No matter what the mass distribution is, the five lenses PG1115+080, SBS1520+530, B1600+434, PKS1830-211, ⁶ and HE2149-2745 have very similar dark matter halos. For a fixed slope , the five systems are consistent with a common value for the surface density of

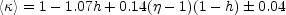(B.99)

where H₀ = 100h km s^-1 Mpc^-1 and there is an upper limit of 0.07 on the intrinsic scatter of <>. Thus, time delay lenses provide a new window into the structure and homogeneity of dark matter halos, regardless of the actual value of H₀.

There is an enormous range of parametric models that can illustrate how the extent of the halo affects <> and hence H₀ - the pseudo-Jaffe model we used above is only one example. It is useful, however, to use a physically motivated model where the lens galaxy is embedded in a standard NFW (Navarro, Frenk, & White 1996) profile halo as we discussed at the end of Section B.4.1. The lens galaxy consists of the baryons that have cooled to form stars, so the mass of the visible galaxy can be parameterized using the cold baryon fraction f_{b, cold} of the halo, and for these CDM halo models the value of <> is controlled by the cold baryon fraction (Kochanek [2003a]). A constant M/L model is the limit f_{b, cold} 1 (with <> 0.2, 3). Since the baryonic mass fraction of a CDM halo should not exceed the global fraction of f_b 0.17 ± 0.03 (e.g., Spergel et al. [2003]), we cannot use constant M / L models without also abandoning CDM. As we reduce f_{b, cold}, we are adding mass to an extended halo around the lens, leading to an increase in <> and a decrease in . For f_{b, cold} 0.02 the model closely resembles the SIS model (<> 1/2, 2). If we reduce f_{b, cold} further, the mass distribution begins to approach that of the NFW halo without any cold baryons. Figure B.38 shows how <> and H₀ depend on f_{b, cold} for PG1115+080, SBS1520+530, B1600+434 and HE2149-2745. When f_{b, cold} 0.02, the CDM models have parameters very similar to the SIS model, and we obtain a very similar estimate of H₀ = 52 ± 6 km s^-1 Mpc^-1 (95% confidence). If all baryons cool, and f_{b, cold} = f_b, then we obtain H₀ = 65 ± 6 km s^-1 Mpc^-1 (95% confidence), which is still lower than the Key Project estimates.

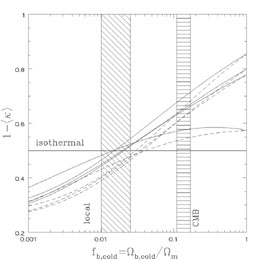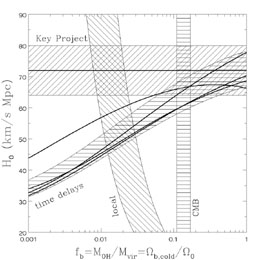Figure B.38. H0 in CDM halo models. The top panel shows 1 - <> for the "simple" lenses (PG1115+080, SBS1520+530, B1600+434, and HE2149-2745) as a function of the cold baryon fraction fb, cold. The solid (dashed) curves include (exclude) the adiabatic compression of the dark matter by the baryons. The horizontal line shows the value for an SIS potential. The bottom panel shows the resulting estimates of H0, where the shaded envelope bracketing the curves is the 95% confidence region for the combined lens sample. The horizontal band shows the Key Project estimate. For larger fb, cold, the density <> decreases and the local slope steepens, leading to larger values of H0. The vertical bands in the two panels show the lower bound on fb from local inventories and the upper bound from the CMB.

We excluded the lenses requiring significantly more complicated models with multiple lens galaxies or very strong perturbations from clusters. If we have yet to reach a consensus on the mass distribution of relatively isolated lenses, it seems premature to extend the discussion to still more complicated systems. We can, however, show that the clusters lenses require significant contributions to <> from the cluster in order to produce the same H₀ as the more isolated systems. As we discussed in Section B.2 the three more complex systems are RXJ0911+0551, Q0957+561 and B1608+656.

RXJ0911+0551 is very strongly perturbed by the nearby X-ray cluster (Morgan et al. [2001]; Hjorth et al. [2002]). Kochanek ([2003b]) found H₀ = 49 ± 5 km s^-1 Mpc^-1 if the primary lens and its satellite were isothermal and H₀ = 67 ± 5 km s^-1 Mpc^-1 if they had constant mass-to-light ratios. The higher value of H₀ = 71 ± 4 km s^-1 Mpc^-1 obtained by Hjorth et al. ([2002]) can be understood by combining Section B.5.1 and Section B.5.2 with the differences in the models. In particular, Hjorth et al. ([2002]) truncated the halo of the primary lens near the Einstein radius and used a lower mass cluster, both of which lower <> and raise H₀. The Hjorth et al. ([2002]) models also included many more cluster galaxies assuming fixed masses and halo sizes.

Q0957+561 is a special case because the primary lens galaxy is the brightest cluster galaxy and it lies nearly at the cluster center (Keeton et al. [2000]; Chartas et al. [2002]). As a result, the lens modeling problems are particularly severe, and Keeton et al. ([2000]) found that all previous models (most recently, Barkana et al. [1999]; Bernstein & Fischer [1999]; and Chae [1999], see Section B.4.6) were incompatible with the observed geometry of the lensed host galaxy. While Keeton et al. ([2000]) found models consistent with the structure of the lensed host, they covered a range of almost ± 25% in their estimates of H₀. A satisfactory treatment of this lens remains elusive.

HE1104-1805 has the most recently measured time delay (Ofek & Maoz [2003], Wyrzykowski et al. [2003]). Given the t = 161 ± 7 day delay, a standard SIE model of this system predicts a very high H₀ 90 km s^-1 Mpc^-1. The geometry of this system and the fact that the inner image is brighter than the outer image both suggest that HE1104-1805 lies in an anomalously high tidal shear field, while the standard model includes a prior to keep the external shear small. A prior is needed because a two-image lens supplies too few constraints to determine both the ellipticity of the main lens and the external shear simultaneously. Since the images and the lens in HE1104-1805 are nearly collinear, the anomalous H₀ estimate for the standard model may be an example of the shear degeneracy we briefly mentioned in Section B.5.1. At present the model surveys needed to understand the new delay have not been made. Observations of the geometry of the host galaxy Einstein ring will resolve any ambiguities due to the shear in the near future (see Section B.10).

The lens B1608+656 consists of two interacting galaxies, and, as we discussed in Section B.2, this leads to a greatly increased parameter space. Fassnacht et al. ([2002]) used SIE models for the two galaxies to find H₀ = 61 - 65 km s^-1 Mpc^-1, depending on whether the lens galaxy positions are taken from the H-band or I-band lens HST images (the statistical errors are negligible). The position differences are probably created by extinction effects from the dust in the lens galaxies. Like isothermal models of the "simple" lenses, the H₀ estimate is below local values, but the disagreement is smaller. These models correctly match the observed time delay ratios. Koopmans et al. ([2003]) obtain a still higher estimate of H₀ = 75 ± 7 km s^-1 Mpc^-1 largely because the lens galaxy positions shift after they include extinction corrections. They use a foreground screen model to make the extinction corrections, which is a better approximation than no extinction corrections, but is unlikely allow precise correction in a system like B1608+656 where the dust and stars are mixed and there is no simple relation between color excess and optical depth (e.g. Witt, Thronson & Capuano [1992]).

Despite recent progress both in modeling the VLBI structure (Wucknitz et al. [2004]) and obtaining deep images (York et al. [2004]) it is unclear whether B0218+357 has escaped its problems with astrometry and models. While York et al. ([2004]) have clearly measured the position of the lens galaxy, the dependence of the position on the choice of the PSF model remains a significant source of uncertainty for estimates of H₀. Models of the system using power law models find a slope very close to isothermal = 2.04 ± 0.02 ( r^-). Unfortunately, these models have too few degrees of freedom given the small astrometric uncertainties in the VLBI structures providing the constraints (because the only angular structure in the model is the ellipsoidal potential used for the main lens galaxy), and this makes the limits on the power slope suspect (see Section B.4.6). For example, while it is true that Lehár et al. ([2000]) estimated that the environmental shear near B0218+357 was small, even a = 0.01 external tidal shear produces deflections (3 milli-arcseconds) that are large compared to the accuracy of the constraints used for the models and so must be included for the models to be reliable. With these caveats, B0218+357 (like the models of B1608+656 with significant extinction corrections) support a nearly isothermal mass distribution with H₀ = 73 ± 8 km s^-1 Mpc^-1.

⁵ This is simply an example. The same behavior would be seen for any other parametric model in which the radial density profile can be adjusted. Back.

⁶ PKS1830-211 is included based on the Winn et al. ([2002b]) model of the HST imaging data as a single lens galaxy. Courbin et al. ([2002]) prefer an interpretation with multiple lens galaxies which would invalidate the analysis. Back.