Olbers was one of a long line of thinkers who pondered the paradox: how can an infinite Universe full of stars not be ablaze with light in every direction? Although cosmologists now speak of galaxies (and other sources of radiation) rather than stars, the question retains its relevance. In fact, the explanation of the intensity of the background radiation at all wavelengths has become recognized as one of the fundamental keys to cosmology. We will begin in this review with what is known about this radiation itself, and then move on to what it tells us about the dark energy and dark matter.
The optical and near-optical (ultraviolet and infrared) portions of the
background comprise what is known as the extragalactic background light
(EBL), the domain of the "classical" Olbers problem. The observed
intensity of background light in these bands guides our understanding
of the way in which the luminous components of the Universe (i.e. the
galaxies) formed and evolved with time.
We now know what Olbers did not: that the main reason why the sky
is dark at night is that the Universe had a beginning in time.
This can be appreciated qualitatively (and quantitatively to within
a factor of a few) with no relativity at all beyond the fact of
a finite speed of light. Imagine yourself at the center of a ball
of glowing gas with radius R and uniform luminosity density
(r) =
0. The intensity
Q of background radiation between you and the edge of the ball is
just
 |
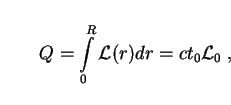(1) |
where we have used R = ct0 as a naive
approximation to the size of the Universe. Thus knowledge of the
luminosity density
0 and
measurement of the background intensity Q tells us
immediately that the galaxies have been shining only for a time
t0.
More refined calculations introduce only minor changes to this result.
Expansion stretches the path length R, but this is more than offset
by the dilution of the luminosity density
(r), which drops
by roughly the same factor cubed. There is a further reduction in
(r) due to the
redshifting of light from distant sources.
So Eq. (1) represents a theoretical upper limit on the
background intensity. In a fully general relativistic treatment, one
obtains the following expression for Q in standard cosmological
models whose scale factor varies as a power-law function of time
(R 
t
):
 |
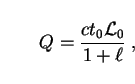(2) |
as may be checked using Eq. (12) in Sec. 2.
Thus Eq. (1) overestimates Q as a function of
t0 by a
factor of 5/3 in a universe filled with dust-like matter
( = 2/3).
Insofar as Q and
0 are both known
quantities, one can in
principle use them to infer a value for t0.
Intensity Q, for instance, is obtained by measuring spectral
intensity
I
()
over the wavelengths where starlight is brightest and integrating:
Q = 
I()
d.
This typically leads to values of around
Q 
1.4 ×
10-4 erg s-1 cm-2
[1].
Luminosity density
0 can be
determined by counting the number of
faint galaxies in the sky down to some limiting magnitude, and extrapolating
to fainter magnitudes based on assumptions about the true distribution
of galaxy luminosities. One finds in this way that
0
1.9 ×
10-32 erg s-1 cm-3
[2].
Alternatively, one can extrapolate from the properties of the Sun,
which emits its energy at a rate per unit mass of
=
L /
M = 1.9
erg s-1 g-1.
A colour-magnitude diagram for nearby stars shows us that the Sun is
modestly brighter than average, with a more typical rate of stellar
energy emission given by about 1/4 the Solar value, or
~ 0.5 erg
s-1 g-1. Multipying this number by
the density of luminous matter in the Universe
(
lum
= 4 × 10-32 g cm-3) gives a figure for mean
luminosity density which is the same as that derived above from galaxy
counts: 0 =
lum
~ 2 × 10-32 erg s-1 cm-3.
Either way, plugging Q and
0 into Eq. (1) with
= 2/3 implies a cosmic age of t0 = 13 Gyr, which differs from
the currently accepted figure by only 5%. (The remaining difference
can be accounted for if cosmic expansion is not a simple power-law
function of time; more on this later.) Thus the brightness of the
night sky tells us not only that there was a big bang, but also roughly
when it occurred. Conversely, the intensity of background radiation
is largely determined by the age of the Universe. Expansion merely deepens
the shade of a night sky that is already black.
We have so far discussed only the bolometric, or integrated intensity
of the background light over all wavelengths, whose significance will
be explored in more detail in Sec. 2. The
spectral background --
from radio to microwave, infrared, optical, ultraviolet, x-ray and
-ray bands
-- represents an even richer store of information
about the Universe and its contents (Fig. 1).
The optical waveband (where galaxies emit most of their light) has been
of particular importance historically, and the infrared band (where the
redshifted light of distant galaxies actually reaches us) has come into
new prominence more recently. By combining the observational data in
both of these bands, we can piece together much of the evolutionary history
of the galaxy population, make inferences about the nature of the
intervening intergalactic medium, and draw conclusions about the dynamical
history of the Universe itself. Interest in this subject has exploded
over the past few years as improvements in telescope and detector
technology have brought us to the threshold of the first EBL detection
in the optical and infrared bands. These developments and their
implications are discussed in Sec. 3.
 |
Figure 1. A compilation of experimental measurements of the intensity of cosmic background radiation at all wavelengths. This figure and the data shown in it will be discussed in more detail in later sections. |
In the remainder of the review, we move on to what the background
radiation tells us about the dark matter and energy, whose current
status is reviewed in Sec. 4. The leading
candidates are taken up individually in
Secs. 5-9.
None of them
are perfectly black. All of them are capable in principle of decaying
into or interacting with ordinary photons, thereby leaving telltale
signatures in the spectrum of background radiation. We begin
with dark energy, for which there is particularly good reason to suspect
a decay with time. The most likely place to look for evidence of such
a process is in the cosmic microwave background, and we review the stringent
constraints that can be placed on any such scenario in
Sec. 5.
Axions, neutrinos and weakly interacting massive particles are treated
next: these particles decay into photons in ways that depend on
parameters such as coupling strength, decay lifetime, and rest mass.
As we show in Secs. 6,
7 and 8,
data in the infrared, optical, ultraviolet, x-ray and
-ray bands
allow us to be specific about the kinds of properties that these
particles must have if they are to make up the dark matter in the Universe.
In Sec. 9, finally, we turn to black
holes. The observed intensity of background radiation, especially in the
-ray band,
is sufficient
to rule out a significant role for standard four-dimensional black holes,
but it may be possible for their higher-dimensional analogs (known as
solitons) to make up all or part of the dark matter. We wrap up our
review in Sec. 10 with some final comments
and a view toward future developments.