4. DARK MATTER AND DARK ENERGY

4.1. The four elements of modern cosmology

Observations of the intensity of extragalactic background light effectively allow us to take a census of one component of the Universe: its luminous matter. In astronomy, where nearly everything we know comes to us in the form of light signals, one might be forgiven for thinking that luminous matter was the only kind that counted. This supposition, however, turns out to be spectacularly wrong. The density _lum of luminous matter is now thought to comprise less than one percent of the total density _tot of all forms of matter and energy put together. [Here as in Secs. 2 and 3, we express densities in units of the critical density, Eq. (24), and denote them with the symbol .] The remaining 99% or more consists of dark matter and energy which, while not seen directly, are inferred to exist from their gravitational influence on luminous matter as well as the geometry of the Universe.

The identity of this unseen substance, whose existence was first suspected by astronomers such as Kapteyn [47], Oort [48] and Zwicky [49], has become the central mystery of modern cosmology. Indirect evidence over the past few years has increasingly suggested that there are in fact four distinct categories of dark matter and energy, three of which imply new physics beyond the existing standard model of particle interactions. This is an extraordinary claim, and one whose supporting evidence deserves to be carefully scrutinized. We devote Sec. 4 to a critical review of this evidence, beginning here with a brief overview of the current situation and followed by a closer look at the arguments for all four parts of nature's "dark side."

At least some of the dark matter, such as that contained in planets and "failed stars" too dim to see, must be composed of ordinary atoms and molecules. The same applies to dark gas and dust (although these can sometimes be seen in absorption, if not emission). Such contributions comprise baryonic dark matter (BDM), which combined together with luminous matter gives a total baryonic matter density of _{bar lum} + _bdm. If our understanding of big-bang theory and the formation of the light elements is correct, then we will see that _bar cannot represent more than 5% of the critical density.

Besides the dark baryons, it now appears that three other varieties of dark matter play a role. The first of these is cold dark matter (CDM), the existence of which has been inferred from the behaviour of visible matter on scales larger than the solar system (e.g., galaxies and clusters of galaxies). CDM is thought to consist of particles (sometimes referred to as "exotic" dark-matter particles) whose interactions with ordinary matter are so weak that they are seen primarily via their gravitational influence. While they have not been detected (and are indeed hard to detect by definition), such particles are predicted in plausible extensions of the standard model. The overall CDM density _cdm is believed by many cosmologists to exceed that of the baryons (_bar) by at least an order of magnitude.

Another piece of the puzzle is provided by neutrinos, particles whose existence is unquestioned but whose collective density () depends on their rest mass, which is not yet known. If neutrinos are massless, or nearly so, then they remain relativistic throughout the history of the Universe and behave for dynamical purposes like photons. In this case neutrino contributions combine with those of photons () to give the present radiation density as _r,0 = + . This is known to be very small. If on the other hand neutrinos are sufficiently massive, then they are no longer relativistic on average, and belong together with baryonic and cold dark matter under the category of pressureless matter, with present density _m,0 = _bar + _cdm + . These neutrinos could play a significant dynamical role, especially in the formation of large-scale structures in the early Universe, where they are sometimes known as hot dark matter (HDM). Recent experimental evidence suggests that neutrinos do contribute to _m,0 but at levels below those of the baryons.

Influential only over the largest scales -- those of the cosmological horizon itself -- is the final component of the unseen Universe: dark energy. Its many alternative names (the zero-point field, vacuum energy, quintessence and the cosmological constant ) testify to the fact that there is currently no consensus as to where dark energy originates, or how to calculate its energy density () from first principles. Existing theoretical estimates of this latter quantity range over some 120 orders of magnitude, prompting many cosmologists until very recently to disregard it altogether. Observations of distant supernovae and CMB fluctuations, however, increasingly imply that dark energy is not only real but that its present energy density (_,0) exceeds that of all other forms of matter (_m,0) and radiation (_r,0) put together.

The Universe described above hardly resembles the one we see. It is composed to a first approximation of invisible dark energy whose physical origin remains obscure. Most of what remains is in the form of CDM particles, whose "exotic" nature is also not yet understood. Close inspection is needed to make out the further contribution of neutrinos, although this too is nonzero. And baryons, the stuff of which we are made, are little more than a cosmic afterthought. This picture, if confirmed, constitutes a revolution of Copernican proportions, for it is not only our location in space which turns out to be undistinguished, but our very makeup. The "four elements" of modern cosmology are shown schematically in Fig. 17.

Figure 17. Top: earth, water, air and fire, the four elements of ancient cosmology (attributed to the Greek philosopher Empedocles). Bottom: their modern counterparts (figure taken from the review in [50]).

4.2. Baryonic dark matter

Let us now go over the evidence for these four species of dark matter more carefully, beginning with the baryons. The total present density of luminous baryonic matter can be inferred from the observed luminosity density of the Universe, if various reasonable assumptions are made about the fraction of galaxies of different morphological type, their ratios of disk-type to bulge-type stars, and so on. A recent and thorough such estimate is [2]:

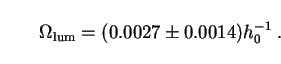(92)

Here h₀ is as usual the value of Hubble's constant expressed in units of 100 km s^-1 Mpc^-1. While this parameter (and hence the experimental uncertainty in H₀) factored out of the EBL intensities in Secs. 2 and 3, it must be squarely faced where densities are concerned. We therefore digress briefly to discuss the observational status of h₀.

Using various relative-distance methods, all calibrated against the distance to Cepheid variables in the Large Magellanic Cloud (LMC), the Hubble Key Project (HKP) team has determined that h₀ = 0.72 ± 0.08 [51]. Independent "absolute" methods (e.g., time delays in gravitational lenses, the Sunyaev-Zeldovich effect and the Baade-Wesselink method applied to supernovae) have higher uncertainties but are roughly consistent with this, giving h₀ 0.55 - 0.74 [52]. This level of agreement is a great improvement over the factor-two discrepancies of previous decades.

There are signs, however, that we are still some way from "precision" values with uncertainties of less than ten percent. A recalibrated LMC Cepheid period-luminosity relation based on a much larger sample (from the OGLE microlensing survey) leads to considerably higher values, namely h₀ = 0.85 ± 0.05 [53]. A purely geometric technique, based on the use of long-baseline radio interferometry to measure the transverse velocity of water masers [54], also implies that the traditional calibration is off, raising all Cepheid-based estimates by 12 ± 9% [55]. This would boost the HKP value to h₀ = 0.81 ± 0.09. There is some independent support for such a recalibration in observations of "red clump stars" [56] and eclipsing binaries [57] in the LMC. New observations at multiple wavelengths, however, suggest that early conclusions based on these arguments may be premature [58].

On this subject, history encourages caution. Where it is necessary to specify the value of h₀ in this review, we will adopt:

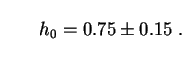(93)

Values at the edges of this range can discriminate powerfully between different cosmological models. This is largely a function of their ages, which can be computed by integrating (36) or (for flat models) directly from Eq. (56). Alternatively, one can integrate the Friedmann-Lemaître equation (33) numerically backward in time. Since this equation defines the expansion rate H / R, its integral gives the scale factor R(t). We plot the results in Fig. 18 for the four cosmological "test models" in Table 2 (EdS, OCDM, CDM, and BDM).

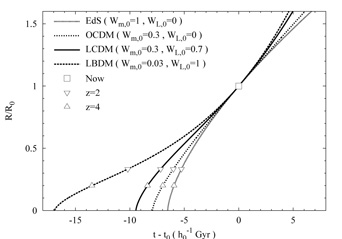Figure 18. Evolution of the cosmological scale factor (t) R(t) / R 0 as a function of time (in Hubble times) for the cosmological test models introduced in Table 2 (Sec. 3). Triangles indicate the range 2 zf 4 where the bulk of galaxy formation may have taken place.

These are seen to have ages of 7h₀^-1, 8h₀^-1, 10h₀^-1 and 17h₀^-1 Gyr respectively. A firm lower limit of 11 Gyr can be set on the age of the Universe by means of certain metal-poor halo stars whose ratios of radioactive ²³²Th and ²³⁸U imply that they formed between 14.1 ± 2.5 Gyr [59] and 15.5 ± 3.2 Gyr ago [60]. If h₀ lies at the upper end of the above range (h₀ = 0.9), then the EdS and OCDM models would be ruled out on the basis that they are not old enough to contain these stars (this is known as the age crisis in low-_,0 models). With h₀ at the bottom of the range (h₀ = 0.6), however, only EdS comes close to being excluded. The EdS model thus defines one edge of the spectrum of observationally viable models.

The BDM model faces the opposite problem: Fig. 18 shows that its age is 17h₀^-1 Gyr, or as high as 28 Gyr (if h₀ = 0.6). The latter number in particular is well beyond the age of anything seen in our Galaxy. Of course, upper limits on the age of the Universe are not as secure as lower ones. But following Copernican reasoning, we do not expect to live in a galaxy which is unusually young. To estimate the age of a "typical" galaxy, we recall from Sec. 3.2 that most galaxies appear to have formed at redshifts 2 z_f 4. The corresponding range of scale factors, from Eq. (13), is 0.33 R / R ₀ 0.2. In the BDM model, Fig. 18 shows that R(t) / R ₀ does not reach these values until (5 ± 2) h₀^-1 Gyr after the big bang. Thus galaxies would have an age of about (12 ± 2) h₀^-1 Gyr in the BDM model, and not more than 21 Gyr in any case. This is close to upper limits which have been set on the age of the Universe in models of this type, t₀ < 24 ± 2 Gyr [61]. Thus the BDM model, or something close to it, probably defines a position opposite that of EdS on the spectrum of observationally viable models.

For the other three models, Fig. 18 shows that galaxy formation must be accomplished within less than 2 Gyr after the big bang. The reason this is able to occur so quickly is that these models all contain significant amounts of CDM, which decouples from the primordial plasma before the baryons and prepares potential wells for the baryons to fall into. This, as we will see, is one of the main motivations for CDM.

Returning now to the density of luminous matter, we find with our values (93) for h₀ that Eq. (92) gives _lum = 0.0036 ± 0.0020. This is the basis for our statement (Sec. 4.1) that the visible components of the Universe account for less than 1% of its density.

It may however be that most of the baryons are not visible. How significant could such dark baryons be? The theory of primordial big-bang nucleosynthesis provides us with an independent method for determining the density of total baryonic matter in the Universe, based on the assumption that the light elements we see today were forged in the furnace of the hot big bang. Results using different light elements are roughly consistent, which is impressive in itself. The primordial abundances of ⁴He (by mass) and ⁷Li (relative to H) imply a baryon density of _bar = (0.010 ± 0.004)h₀^-2 [62]. By contrast, measurements based exclusively on the primordial D/H abundance give a higher value with lower uncertainty: _bar = (0.019 ± 0.002)h₀^-2 [63]. Since it appears premature at present to exclude either of these results, we choose an intermediate value of _bar = (0.016 ± 0.005)h₀^-2. Combining this with our range of values (93) for h₀, we conclude that

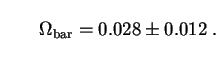(94)

This agrees very well with independent estimates obtained by adding up individual mass contributions from all known repositories of baryonic matter via their estimated mass-to-light ratios [2]. It also provides the rationale for our choice of _m,0 = 0.03 in the BDM model. Eq. (94) implies that all the atoms and molecules in existence make up less than 5% of the critical density.

The vast majority of these baryons, moreover, are invisible. Using Eqs. (92) and (93) together with the above-mentioned value of _bar h₀², we infer a baryonic dark matter fraction _bdm / _bar = 1 - _lum / _bar = (87 ± 8)%. Where do these dark baryons reside? One possibility is that they are smoothly distributed in a gaseous intergalactic medium, which would have to be strongly ionized in order to explain why it has not left a more obvious absorption signature in the light from distant quasars. Observations using OVI absorption lines as a tracer of ionization suggest that the contribution of such material to _bar is at least 0.003h₀^-1 [64], comparable to _lum. Simulations are able to reproduce many observed features of the "forest" of Lyman- (Ly) absorbers with as much as 80 - 90% of the baryons in this form [65].

Dark baryonic matter could also be bound up in clumps of matter such as substellar objects (jupiters, brown dwarfs) or stellar remnants (white, red and black dwarfs, neutron stars, black holes). Substellar objects are not likely to make a large contribution, given their small masses. Black holes are limited in the opposite sense: they cannot be more massive than about 10⁵ M since this would lead to dramatic tidal disruptions and lensing effects which are not seen [66]. The baryonic dark-matter clumps of most interest are therefore ones whose mass is within a few orders of M. Gravitational microlensing constraints based on quasar variability do not seriously limit such objects at present, setting an upper bound of 0.1 (well above _bar) on their combined contributions to _m,0 in an EdS Universe [67].

The existence of at least one class of compact dark objects, the massive compact halo objects (MACHOs), has been confirmed within our own galactic halo by the MACHO microlensing survey of LMC stars [68]. The inferred lensing masses lie in the range (0.15 - 0.9) M and would account for between 8% and 50% of the high rotation velocities seen in the outer parts of the Milky Way, depending on a choice of halo model. If the halo is spherical, isothermal and isotropic, then at most 25% of its mass can be ascribed to MACHOs, according to a complementary survey (EROS) of microlensing in the direction of the SMC [69]. The identity of the lensing bodies discovered in these surveys has been hotly debated. White dwarfs are unlikely candidates, since we see no telltale metal-rich ejecta from their massive progenitors [70]. Low-mass red dwarfs would have to be older and/or fainter than usually assumed, based on the numbers seen so far [71]. Degenerate "beige dwarfs" that could form above the theoretical hydrogen-burning mass limit of 0.08M without fusing have been proposed as an alternative [72], but it appears that such stars would form far too slowly to be important [73].

4.3. Cold dark matter

The introduction of a second species of unseen dark matter into the Universe has been justified on three main grounds: (1) a range of observational arguments imply that the total density parameter of gravitating matter exceeds that provided by baryons and bound neutrinos; (2) our current understanding of the growth of large-scale structure (LSS) requires the process to be helped along by large quantities of non-relativistic, weakly interacting matter in the early Universe, creating the potential wells for infalling baryons; and (3) theoretical physics supplies several plausible (albeit still undetected) candidate CDM particles with the right properties.

Since our ideas on structure formation may change, and the candidate particles may not materialize, the case for cold dark matter turns at present on the observational arguments. At one time, these were compatible with _cdm 1, raising hopes that CDM would resolve two of the biggest challenges in cosmology at a single stroke: accounting for LSS formation and providing all the dark matter necessary to make _m,0 = 1, vindicating the EdS model (and with it, the simplest models of inflation). Observations, however, no longer support values of _m,0 this high, and independent evidence now points to the existence of at least two other forms of matter-energy beyond the standard model (neutrinos and dark energy). The CDM hypothesis is therefore no longer as compelling as it once was. With this in mind we will pay special attention to the observational arguments in this section. The lower limit on _m,0 is crucial: only if _m,0 > _bar + do we require _cdm > 0.

The arguments can be broken into two classes: those which are purely empirical, and those which assume in addition the validity of the gravitational instability (GI) theory of structure formation. Let us begin with the empirical arguments. The first has been mentioned already in Sec. 4.2: the spiral galaxy rotation curve. If the MACHO and EROS results are taken at face value, and if the Milky Way is typical, then compact objects make up less than 50% of the mass of the halos of spiral galaxies. If, as has been argued [74], the remaining halo mass cannot be attributed to baryonic matter in known forms such as dust, rocks, planets, gas, or hydrogen snowballs, then a more exotic form of dark matter is required.

The total mass of dark matter in galaxies, however, is limited. The easiest way to see this is to compare the mass-to-light ratio (M / L) of our own Galaxy to that of the Universe as a whole. If the latter has the critical density, then its M / L-ratio is just the ratio of the critical density to its luminosity density: (M / L)_crit,0 = _crit,0 / ₀ = (1040 ± 230) M / L, where we have used (20) for ₀, (24) for _crit,0 and (93) for h₀. The corresponding value for the Milky Way is (M / L)_mw = (21 ± 7) M / L, since the latter's luminosity is L_mw = (2.3 ± 0.6) × 10¹⁰ L (in the B-band) and its total dynamical mass (including that of any unseen halo component) is M_mw = (4.9 ± 1.1) × 10¹¹ M inside 50 kpc from the motions of Galactic satellites [75]. The ratio of (M / L)_mw to (M / L)_crit,0 is thus less than 3%, and even if we multiply this by a factor of a few to account for possible halo mass outside 50 kpc, it is clear that galaxies like our own cannot make up more than 10% of the critical density.

Most of the mass of the Universe, in other words, is spread over scales larger than galaxies, and it is here that the arguments for CDM take on the most force. The most straightforward of these involve further applications of the mass-to-light ratio: one measures M / L for a chosen region, corrects for the corresponding value in the "field," and divides by (M / L)_crit,0 to obtain _m,0. Much, however, depends on the choice of region. A widely respected application of this approach is that of the CNOC team [76], which uses rich clusters of galaxies. These systems sample large volumes of the early Universe, have dynamical masses which can be measured by three independent methods (the virial theorem, x-ray gas temperatures and gravitational lensing), and are subject to reasonably well-understood evolutionary effects. They are found to have M / L ~ 200 M / L on average, giving _m,0 = 0.19 ± 0.06 when _,0 = 0 [76]. This result scales as (1 - 0.4_,0) [77], so that _m,0 drops to 0.11 ± 0.04 in a model with _,0 = 1.

The weak link in this chain of inference is that rich clusters may not be characteristic of the Universe as a whole. Only about 10% of galaxies are found in such systems. If individual galaxies (like the Milky Way, with M / L 21M / L) are substituted for clusters, then the inferred value of _m,0 drops by a factor of ten, approaching _bar and removing the need for CDM. An effort to address the impact of scale on M / L arguments has led to the conclusion that _m,0 = 0.16 ± 0.05 (for flat models) when regions of all scales are considered from individual galaxies to superclusters [78].

Another line of argument is based on the cluster baryon fraction, or ratio of baryonic-to-total mass (M_bar / M_tot) in galaxy clusters. Baryonic matter is defined as the sum of visible galaxies and hot gas (the mass of which can be inferred from x-ray temperature data). Total cluster mass is measured by the above-mentioned methods (virial theorem, x-ray temperature, or gravitational lensing). At sufficiently large radii, the cluster may be taken as representative of the Universe as a whole, so that _m,0 = _bar / (M_bar / M_tot), where _bar is fixed by big-bang nucleosynthesis (Sec. 4.2). Applied to various clusters, this procedure leads to _m,0 = 0.3 ± 0.1 [79]. This result is probably an upper limit, partly because baryon enrichment is more likely to take place inside the cluster than out, and partly because dark baryonic matter (such as MACHOs) is not taken into account; this would raise M_bar and lower _m,0.

Other direct methods of constraining the value of _m,0 are rapidly becoming available, including those based on the evolution of galaxy cluster x-ray temperatures [80], radio galaxy lobes as "standard rulers" in the classical angular size-distance relation [81] and distortions in the images of distant galaxies due to weak gravitational lensing by intervening large-scale structures [82]. In combination with other evidence, especially that based on the SNIa magnitude-redshift relation and the CMB power spectrum (to be discussed shortly), these techniques show considerable promise for reducing the uncertainty in the matter density.

We move next to measurements of _m,0 based on the assumption that the growth of LSS proceeded via gravitational instability from a Gaussian spectrum of primordial density fluctuations (GI theory for short). These argmuents are circular in the sense that such a process could not have taken place as it did unless _m,0 is considerably larger than _bar. But inasmuch as GI theory is the only structure-formation theory we have which is both fully worked out and in good agreement with observation (with some difficulties on small scales [83]), this way of determining _m,0 should be taken seriously.

According to GI theory, the formation of large-scale structures is more or less complete by z _m,0^-1 - 1 [84]. Therefore, one way to constrain _m,0 is to look for number density evolution in large-scale structures such as galaxy clusters. In a low-matter-density Universe, this would be relatively constant out to at least z ~ 1, whereas in a high-matter-density Universe one would expect the abundance of clusters to drop rapidly with z because they are still in the process of forming. The fact that massive clusters are seen at redshifts as high as z = 0.83 has been used to infer that _m,0 = 0.17^+0.14_-0.09 for _,0 = 0 models, and _m,0 = 0.22^+0.13_-0.07 for flat ones [85].

Studies of the power spectrum P(k) of the distribution of galaxies or other structures can be used in a similar way. In GI theory, structures of a given mass form by the collapse of large volumes in a low-matter-density Universe, or smaller volumes in a high-matter-density Universe. Thus _m,0 can be constrained by changes in P(k) between one redshift and another. Comparison of the mass power spectrum of Ly absorbers at z 2.5 with that of local galaxy clusters at z = 0 has led to an estimate of _m,0 = 0.46^+0.12_-0.10 for _,0 = 0 models [86]. This result goes as approximately (1 - 0.4_,0), so that the central value of _m,0 drops to 0.34 in a flat model, and 0.28 if _,0 = 1. One can also constrain _m,0 from the local galaxy power spectrum alone, although this involves some assumptions about the extent to which "light traces mass" (i.e. to which visible galaxies trace the underlying density field). Results from the 2dF survey give _m,0 = 0.29^+0.12_-0.11 assuming h₀ = 0.7 ± 0.1 [87] (here and elsewhere we quote 95% or 2 confidence levels where these can be read from the data, rather than the more commonly reported 68% or 1 limits). A preliminary best fit from the Sloan Digital Sky Survey (SDSS) is _m,0 = 0.19^+0.19_-0.11 [88]. As we discuss below, there are good prospects for reducing this uncertainty by combining data from galaxy surveys of this kind with CMB data [89], though such results must be interpreted with care at present [90].

A third group of measurements, and one which has traditionally yielded the highest estimates of _m,0, comes from the analysis of galaxy peculiar velocities. These are generated by the gravitational potential of locally over or under-dense regions relative to the mean matter density. The power spectra of the velocity and density distributions can be related to each other in the context of GI theory in a way which depends explicitly on _m,0. Tests of this kind probe relatively small volumes and are hence insensitive to _,0, but they can depend significantly on h₀ as well as the spectral index n of the density distribution. In [91], where the latter is normalized to CMB fluctuations, results take the form _m,0 h₀^1.3n² 0.33 ± 0.07 or (taking n = 1 and using our values of h₀) _m,0 0.48 ± 0.15.

In summarizing these results, one is struck by the fact that arguments based on gravitational instability (GI) theory favour values of _m,0 0.2 and higher, whereas purely empirical arguments require _m,0 0.4 and lower. The latter are in fact compatible in some cases with values of _m,0 as low as _bar, raising the possibility that CDM might not in fact be necessary. The results from GI-based arguments, however, cannot be stretched this far. What is sometimes done is to "go down the middle" and blend the results of both kinds of arguments into a single bound of the form _m,0 0.3 ± 0.1. Any such bound with _m,0 > 0.05 constitutes a proof of the existence of CDM, since _bar 0.04 from (94). (Neutrinos only strengthen this argument, as we note in Sec. 4.4.) A more conservative interpretation of the data, bearing in mind the full range of _m,0 values implied above (_{bar m,0} 0.6), is

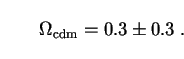(95)

But it should be stressed that values of _cdm at the bottom of this range carry with them the (uncomfortable) implication that the conventional picture of structure formation via gravitational instability is incomplete. Conversely, if our current understanding of structure formation is correct, then CDM must exist and _cdm > 0.

The question, of course, becomes moot if CDM is discovered in the laboratory. From a large field of theoretical particle candidates, two have emerged as frontrunners: axions and supersymmetric weakly-interacting massive particles (WIMPs). The plausibility of both candidates rests on three properties: they are (1) weakly interacting (i.e. "noticed" by ordinary matter primarily via their gravitational influence); (2) cold (i.e. non-relativistic in the early Universe, when structures began to form); and (3) expected on theoretical grounds to have a collective density within a few orders of magnitude of the critical one. We will return to these particles in Secs. 6 and 8 respectively.

4.4. Massive neutrinos

Since neutrinos indisputably exist in great numbers, they have been leading dark-matter candidates for longer than axions or WIMPs. They gained prominence in 1980 when teams in the U.S.A. and the Soviet Union both reported evidence of nonzero neutrino rest masses. While these claims did not stand up, a new round of experiments once again indicates that m (and hence ) > 0.

The neutrino number density n per species is 3/11 that of the CMB photons. Since the latter are in thermal equilibrium, their number density is n_cmb = 2(3)(kT_cmb / c)³ / ² [92] where (3) = 1.202. Multiplying by 3/11 and dividing through by the critical density (24), we obtain

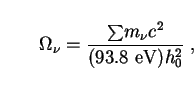(96)

where the sum is over three neutrino species. We follow convention and specify particle masses in units of eV / c², where 1 eV / c² = 1.602 × 10^-12 erg / c² = 1.783 × 10^-33 g. The calculations in this section are strictly valid only for m c² 1 MeV. More massive neutrinos with m c² ~ 1 GeV were once considered as CDM candidates but are no longer viable since experiments at the LEP collider rule out additional neutrino species with masses up to at least half of that of the Z₀ (m_Z0 c² = 91 GeV).

Current laboratory upper bounds on neutrino rest masses are m_e c² < 3 eV, m_µ c² < 0.19 MeV and m c² < 18 MeV, so it would appear feasible in principle for these particles to close the Universe. In fact m_µ and m are limited far more stringently by (96) than by laboratory bounds. Perhaps the best-known theory along these lines is that of Sciama [93], who postulated a population of -neutrinos with m c² 29 eV. Eq. (96) shows that such neutrinos would account for much of the dark matter, contributing a minimum collective density of 0.38 (assuming as usual that h₀ 0.9). We will consider decaying neutrinos further in Sec. 7.

Strong upper limits can be set on within the context of the gravitational instability picture. Neutrinos constitute hot dark matter (i.e. they are relativistic when they decouple from the primordial fireball) and are therefore able to stream freely out of density perturbations in the early Universe, erasing them before they have a chance to grow and suppressing the power spectrum P(k) of density fluctuations on small scales k. Agreement between LSS theory and observation can be achieved in models with as high as 0.2, but only in combination with values of the other cosmological parameters that are no longer considered realistic (e.g. _bar + _cdm = 0.8 and h₀ = 0.5) [94]. A recent 95% confidence-level upper limit on the neutrino density based on data from the 2dF galaxy survey reads [95]

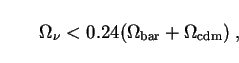(97)

if no prior assumptions are made about the values of _m,0, _bar, h₀ and n. When combined with Eqs. (94) and (95) for _bar and _cdm, this result implies that < 0.15. Thus if structure grows by gravitational instability as generally assumed, then neutrinos may still play a significant, but not dominant role in cosmological dynamics. Note that neutrinos lose energy after decoupling and become nonrelativistic on timescales t_nr 190, 000 yr (m c²/eV)^-2 [96], so that Eq. (97) is quite consistent with our neglect of relativistic particles in the Friedmann-Lemaître equation (Sec. 2.3).

Lower limits on follow from a spectacular string of neutrino experiments employing particle accelerators (LSND [97]), cosmic rays in the upper atmosphere (Super-Kamiokande [98]), the flux of neutrinos from the Sun (SAGE [99], Homestake [100], GALLEX [101], SNO [102]), nuclear reactors (KamLAND [103]) and, most recently, directed neutrino beams (K2K [104]). The evidence in each case points to interconversions between species known as neutrino oscillations, which can only take place if all species involved have nonzero rest masses. It now appears that oscillations occur between at least two neutrino mass eigenstates whose masses squared differ by ₂₁² | m₂² - m₁²| = 6.9^+1.5_-0.8 × 10^-5 eV² / c⁴ and ₃₁² | m₃² - m₁²| = 2.3^+0.7_-0.9 × 10^-3 eV² / c⁴ [105]. Scenarios involving a fourth "sterile" neutrino were once thought to be needed but are disfavoured by global fits to all the data. Oscillation experiments are sensitive to mass differences, and cannot fix the mass of any one neutrino flavour unless they are combined with another experiment such as neutrinoless double-beta decay [106]. Nevertheless, if neutrino masses are hierarchical, like those of other fermions, then one can take m₃ >> m₂ >> m₁ so that the above measurements impose a lower limit on total neutrino mass: m c² > 0.045 eV. Putting this number into (96), we find that

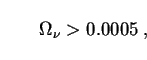(98)

with h₀ 0.9 as usual. If, instead, neutrino masses are nearly degenerate, then could in principle be larger than this, but will in any case still lie below the upper bound (97) imposed by structure formation. The neutrino contribution to _tot,0 is thus anywhere from about one-tenth that of luminous matter (Sec. 4.2) to about one-quarter of that attributed to CDM (Sec. 4.3). We emphasize that, if _cdm is small, then must be small also. In theories (like that to be discussed in Sec. 7) where the density of neutrinos exceeds that of other forms of matter, one would need to modify the standard gravitational instability picture by encouraging the growth of structure in some other way, as for instance by "seeding" them with loops of cosmic string.

4.5. Dark energy

There are at least four reasons to include a cosmological constant () in Einstein's field equations. The first is mathematical: plays a role in these equations similar to that of the additive constant in an indefinite integral [107]. The second is dimensional: specifies the radius of curvature R ^-1/2 in closed models at the moment when the matter density parameter _m goes through its maximum, providing a fundamental length scale for cosmology [108]. The third is dynamical: determines the asymptotic expansion rate of the Universe according to Eq. (34). And the fourth is material: is related to the energy density of the vacuum via Eq. (23).

With so many reasons to take this term seriously, why was it ignored for so long? Einstein himself set = 0 in 1931 "for reasons of logical economy," because he saw no hope of measuring this quantity experimentally at the time. He is often quoted as adding that its introduction in 1915 was the "biggest blunder" of his life. This comment (which was attributed to him by Gamow [109] but does not appear anywhere in his writings), is sometimes interpreted as a rejection of the very idea of a cosmological constant. It more likely represents Einstein's rueful recognition that, by invoking the -term solely to obtain a static solution of the field equations, he had narrowly missed what would surely have been one of the greatest triumphs of his life: the prediction of cosmic expansion.

The relation between and the energy density of the vacuum has led to a quandary in more recent times: modern quantum field theories such as quantum chromodynamics (QCD), electroweak (EW) and grand unified theories (GUTs) imply values for and _,0 that are impossibly large (Table 3). This "cosmological-constant problem" has been reviewed by many people, but there is no consensus on how to solve it [110]. It is undoubtedly another reason why some cosmologists have preferred to set = 0, rather than deal with a parameter whose physical origins are still unclear.

Table 3. Theoretical Estimates of _,0

Theory	Predicted value of	,0
QCD	(0.3 GeV)4 -3 c-5 = 1016 g cm-3	1044 h0-2
EW	(200 GeV)4 -3 c-5 = 1026 g cm-3	1055 h0-2
GUTs	(1019 GeV)4 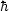-3 c-5 = 1093 g cm-3	10122 h0-2

One suggestion for understanding the possible nature of such a cancellation has been to treat the vacuum energy field literally as an Olbers-type summation of contributions from different places in the Universe [111]. It can then be handled with the same formalism that we have developed in Secs. 2 and 3 for background radiation. This has the virtue of framing the problem in concrete terms, and raises some interesting possibilities, but does not in itself explain why the energy density inherent in such a field does not gravitate in the conventional way [112].

Another idea is that theoretical expectations for the value of might refer only to the latter's "bare" value, which could have been progressively "screened" over time. The cosmological constant then becomes a variable cosmological term [113]. In such a scenario the "low" value of _,0 merely reflects the fact that the Universe is old. In general, however, this means modifying Einstein's field equations and/or introducing new forms of matter such as scalar fields. We look at this suggestion in more detail in Sec. 5.

A third possibility occurs in higher-dimensional gravity, where the cosmological constant can arise as an artefact of dimensional reduction (i.e. in extracting the appropriate four-dimensional limit from the theory). In such theories the "effective" ₄ may be small while its N-dimensional analog _N is large [114]. We consider some aspects of higher-dimensional gravity in Sec. 9.

As a last recourse, some workers have argued that might be small "by definition," in the sense that a universe in which was large would be incapable of giving rise to intelligent observers like ourselves [115]. This is an application of the anthropic principle whose status, however, remains unclear.

4.6. Cosmological concordance

Let us pass to what is known about the value of _,0 from cosmology. It is widely believed that the Universe originated in a big bang singularity rather than passing through a "big bounce" at the beginning of the current expansionary phase. By differentiating the Friedmann-Lemaître equation (33) and setting the expansion rate and its time derivative to zero, one obtains an upper limit (sometimes called the Einstein limit _,E) on _,0 as a function of _m,0. For _m,0 = 0.3 the requirement that _,0 < _,E implies _,0 < 1.71, a limit that tightens to _,0 < 1.16 for _m,0 = 0.03 [1].

A slightly stronger constraint can be formulated (for closed models) in terms of the antipodal redshift. The antipodes are the set of points located at = , where (radial coordinate distance) is related to r by d = (1 - kr²)^-1/2 dr. Using (9) and (14) this can be rewritten in the form d = - (c / H₀ R ₀) dz / 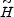(z) and integrated with the help of (33). Gravitational lensing of sources beyond the antipodes cannot give rise to normal (multiple) images [116], so the redshift z_a of the antipodes must exceed that of the most distant normally-lensed object, currently a protogalaxy at z = 10.0 [117]. Requiring that z_a > 10.0 leads to the upper bound _,0 < 1.51 if _m,0 = 0.3. This tightens to _,0 < 1.13 for BDM-type models with _m,0 = 0.03.

The statistics of gravitational lenses lead to a different and stronger upper limit which applies regardless of geometry. The increase in path length to a given redshift in vacuum-dominated models (relative to, say, EdS) means that there are more sources to be lensed, and presumably more lensed objects to be seen. The observed frequency of lensed quasars, however, is rather modest, leading to an early bound of _,0 < 0.66 for flat models [118]. Dust could hide distant sources [119]. However, radio lenses should be far less affected, and these give only slightly weaker constraints: _,0 < 0.73 (for flat models) or _,0 0.4 + 1.5_m,0 (for curved ones) [120]. Recent indications are that this method loses much of its sensitivity to _,0 when assumptions about the lensing population are properly normalized to galaxies at high redshift [121]. A new limit from radio lenses in the Cosmic Lens All-Sky Survey (CLASS) is _,0 < 0.89 for flat models [122].

Tentative lower limits have been set on _,0 using faint galaxy number counts. This premise is similar to that behind lensing statistics: the enhanced comoving volume at large redshifts in vacuum-dominated models should lead to greater (projected) galaxy number densities at faint magnitudes. In practice, it has proven difficult to disentangle this effect from galaxy luminosity evolution. Early claims of a best fit at _,0 0.9 [123] have been disputed on the basis that the steep increase seen in numbers of blue galaxies is not matched in the K-band, where luminosity evolution should be less important [124]. Attempts to account more fully for evolution have subsequently led to a lower limit of _,0 > 0.53 [125], and most recently a reasonable fit (for flat models) with a vacuum density parameter of _,0 = 0.8 [42].

Other evidence for a significant _,0-term has come from numerical simulations of large-scale structure formation. Fig. 19 shows the evolution of massive structures between z = 3 and z = 0 in simulations by the VIRGO Consortium [126]. The CDM model (top row) provides a qualitatively better match to the observed distribution of galaxies than EdS ("SCDM," bottom row). The improvement is especially marked at higher redshifts (left-hand panels). Power spectrum analysis, however, reveals that the match is not particularly good in either case [126]. This could reflect bias (i.e. systematic discrepancy between the distributions of mass and light). Different combinations of _m,0 and _,0 might also provide better fits. Simulations of closed BDM-type models would be of particular interest [11, 50, 127].

Figure 19. Numerical simulations of structure formation. In the top row is the CDM model with m,0 = 0.3, ,0 = 0.7 and h0 = 0.7. The bottom row shows the EdS ("SCDM") model with m,0 = 1, ,0 = 0 and h0 = 0.5. The panel size is comoving with the Hubble expansion, and time runs from left (z = 3) to right (z = 0). (Images courtesy of J. Colberg and the VIRGO Consortium).

The first measurements to put both lower and upper bounds on _,0 have come from Type Ia supernovae (SNIa). These objects are very bright, with luminosities that are consistent (when calibrated against rise time), and they are not thought to evolve significantly with redshift. All of these properties make them ideal standard candles for use in the magnitude-redshift relation. In 1998 and 1999 two independent groups (HZT [128] and SCP [129]) reported a systematic dimming of SNIa at z 0.5 by about 0.25 magnitudes relative to that expected in an EdS model, suggesting that space at these redshifts is "stretched" by dark energy. These programs have now expanded to encompass more than 200 supernovae, with results that can be summarized in the form of a 95% confidence-level relation between _m,0 and _,0 [130]:

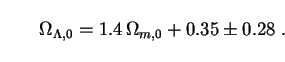(99)

Such a relationship is inconsistent with the EdS and OCDM models, which have large values of _m,0 with _,0 = 0. To extract quantitative limits on _,0 alone, we recall that _{m,0 bar} 0.02 (Sec. 4.2) and _m,0 0.6 (Sec. 4.3). Interpreting these constraints as conservatively as possible (i.e. _m,0 = 0.31 ± 0.29), we infer from (99) that

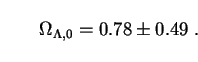(100)

This is not a high-precision measurement, but it is enough to establish that _,0 0.29 and hence that the dark energy is real. New supernovae observations continue to reinforce this conclusion [131]. Not all cosmologists are yet convinced, however, and a healthy degree of caution is still in order regarding a quantity whose physical origin is so poorly understood. Alternative explanations can be constructed that fit the observations by means of "grey dust" [132] or luminosity evolution [133], though these must be increasingly fine-tuned to match new SNIa data at higher redshifts [134]. Much also remains to be learned about the physics of supernova explosions. The shape of the magnitude-redshift relation suggests that observations may have to reach z ~ 2 routinely in order to be able to discriminate statistically between models (like CDM and BDM) with different ratios of _m,0 to _,0.

Further support for the existence of dark energy has arisen from a completely independent source: the angular power spectrum of CMB fluctuations. These are produced by density waves in the primordial plasma, "the oldest music in the Universe" [135]. The first peak in their power spectrum picks out the angular size of the largest fluctuations in this plasma at the moment when the Universe became transparent to light. Because it is seen through the "lens" of a curved Universe, the location of this peak is sensitive to the latter's total density _tot,0 = _,0 + _m,0. Beginning in 2000, a series of increasingly precise measurements of _tot,0 have been reported from experiments including BOOMERANG [136], MAXIMA [137], DASI [138] and most recently the WMAP satellite. The latter's results can be summarized as follows [139] (at the 95% confidence level, assuming h₀ > 0.5):

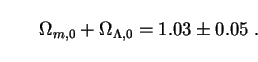(101)

The Universe is therefore spatially flat, or very close to it. To extract a value for _,0 alone, we can do as in the SNIa case and substitute our matter density bounds (_m,0 = 0.31 ± 0.29) into (101) to obtain

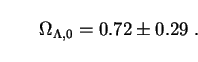(102)

This is consistent with (100), but has error bars which have been reduced by almost half, and are now due entirely to the uncertainty in _m,0. This measurement is impervious to most of the uncertainties of the earlier ones, because it leapfrogs "local" systems whose interpretation is complex (supernovae, galaxies, and quasars), going directly back to the radiation-dominated era when physics was simpler. Eq. (102) is sufficient to establish that _,0 0.43, and hence that dark energy not only exists, but probably dominates the energy density of the Universe.

The CMB power spectrum favours vacuum-dominated models, but is not yet resolved with sufficient precision to discriminate (on its own) between models which have exactly the critical density (like CDM) and those which are close to the critical density (like BDM). As it stands, the location of the first peak in these data actually hints at "marginally closed" models, although the implied departure from flatness is not statistically significant and could also be explained in other ways [141].

Much attention is focused on the higher-order peaks of the spectrum, which contain valuable clues about the matter component. Odd-numbered peaks are produced by regions of the primordial plasma which have been maximally compressed by infalling material, and even ones correspond to maximally rarefied regions which have rebounded due to photon pressure. A high baryon-to-photon ratio enhances the compressions and retards the rarefractions, thus suppressing the size of the second peak relative to the first. The strength of this effect depends on the fraction of baryons (relative to the more weakly-bound neutrinos and CDM particles) in the overdense regions. The BOOMERANG and MAXIMA data show an unexpectedly weak second peak. While there are a number of ways to account for this in CDM models (e.g., by "tilting" the primordial spectrum), the data are fit most naturally by a "no-CDM" BDM model with _cdm = 0, _m,0 = _bar and _,0 1 [142]. Models of this kind have been discussed for some time in connection with analyses of the Lyman- forest of quasar absorption lines [50, 143]. The WMAP data show a stronger second peak and are fit by both CDM and BDM-type models [144]. Data from the upcoming PLANCK satellite should settle this issue.

The best constraints on _,0 come from taking both the supernovae and microwave background results at face value, and substituting one into the other. This provides a valuable cross-check on the matter density, because the SNIa and CMB constraints are very nearly orthogonal in the _m,0-_,0 plane (Fig. 20).

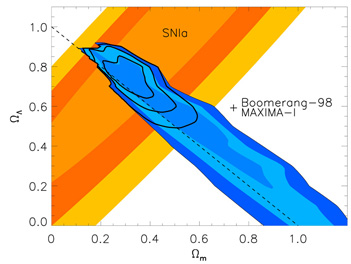Figure 20. Observational constraints on the values of m,0 and ,0 from both SNIa and CMB observations (BOOMERANG, MAXIMA). Shown are 68%, 95% and 99.7% confidence intervals inferred both separately and jointly from the data. (Reprinted from [140] by permission of A. Jaffe and P. L. Richards.)

Thus, forgetting all about our conservative bounds on _m,0 and merely substituting (101) into (99), we find

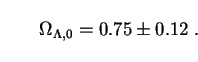(103)

Alternatively, extracting the matter density parameter, we obtain

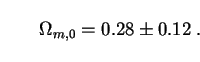(104)

These results further tighten the case for a universe dominated by dark energy. Eq. (103) also implies that _,0 0.87, which begins to put pressure on models of the BDM type. Perhaps most importantly, Eq. (104) establishes that _m,0 0.16, which is inconsistent with BDM and requires the existence of CDM. Moreover, the fact that the range of values picked out by (104) agrees so well with that derived in Sec. 4.3 constitutes solid evidence for the CDM model in particular, and for the gravitational instability picture of large-scale structure formation in general.

The depth of the change in thinking that has been triggered by these developments on the observational side can hardly be exaggerated. Only a few years ago, it was still routine to set = 0 and cosmologists had two main choices: the "one true faith" (flat, with _m,0 1), or the "reformed" (open, with individual believers being free to choose their own values near _m,0 0.3). All this has been irrevocably altered by the CMB experiments. If there is a guiding principle now, it is no longer _m,0 0.3, and certainly not _,0 = 0; it is _tot,0 1 from the power spectrum of the CMB. Cosmologists have been obliged to accept a -term, and it is not so much a question of whether or not it dominates the energy budget of the Universe, but by how much.

4.7. The coincidental Universe

The observational evidence reviewed in the foregoing sections has led us into the corner of parameter space occupied by vacuum-dominated models with close to (or exactly) the critical density. The resulting picture is self-consistent, and agrees with nearly all the data. Major questions, however, remain on the theoretical side. Prime among these is the problem of the cosmological constant, which (as described above) is particularly acute in models with nonzero values of , because one can no longer hope that a simple symmetry of nature will eventually be found which requires = 0.

A related concern has to do with the evolution of the matter and dark-energy density parameters _m and over time. Eqs. (24) and (32) can be combined to give

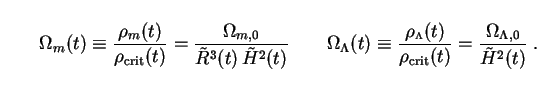(105)

Here [z(t)] is given by (33) as usual and z(t) = 1 / (t) - 1 from (13). Eqs. (105) can be solved exactly for flat models using (54) and (55) for (t) and (t). Results for the CDM model are illustrated in Fig. 21(a).

Figure 21. The evolution of m(t) and (t) in vacuum-dominated models. Panel (a) shows a single model (CDM) over twenty powers of time in either direction. Plotted this way, we are seen to live at a very special time (marked "Now"). Standard nucleosynthesis (tnuc ~ 1 s) and matter-radiation decoupling times (tdec ~ 1011 s) are included for comparison. Panel (b) shows both the CDM and BDM models on a linear rather than logarithmic scale, for the first 100h0-1 Gyr after the big bang (i.e. the lifetime of the stars and galaxies).

What is remarkable in this figure is the location of the present (marked "Now") in relation to the values of _m and . We have apparently arrived on the scene at the precise moment when these two parameters are in the midst of switching places. (We have not considered radiation density _r here, but similar considerations apply to it.) This has come to be known as the coincidence problem, and Carroll [110] has aptly described such a universe as "preposterous," writing: "This scenario staggers under the burden of its unnaturalness, but nevertheless crosses the finish line well ahead of any of its competitors by agreeing so well with the data." Cosmology may be moving toward a position like that of particle physics, where a standard model accounts for all observed phenomena to high precision, but appears to be founded on a series of finely-tuned parameter values which leave one with the distinct impression that the underlying reality has not yet been grasped.

Fig. 21(b) is a close-up view of Fig. 21(a), with one difference: it is plotted on a linear scale in time for the first 100h₀^-1 Gyr after the big bang, rather than a logarithmic scale over 10^±20h₀^-1 Gyr. The rationale for this is simple: 100 Gyr is approximately the lifespan of the galaxies (as determined by their main-sequence stellar populations). One would not, after all, expect observers to appear on the scene long after all the galaxies had disappeared, or in the early stages of the expanding fireball. Seen from the perspective of Fig. 21(b), the coincidence, while still striking, is perhaps no longer so preposterous. The CDM model still appears fine-tuned, in that "Now" follows rather quickly on the heels of the epoch of matter-vacuum equality. In the BDM model, _m,0 and _,0 are closer to the cosmological time-averages of _m(t) and (t) (namely zero and one respectively). In such a picture it might be easier to believe that we have not arrived on the scene at a special time, but merely a late one. Whether or not this is a helpful way to approach the coincidence problem is, to a certain extent, a matter of taste.

To summarize the contents of this section: what can be seen with our telescopes constitutes no more than one percent of the density of the Universe. The rest is dark. A small portion (no more than five percent) of this dark matter is made up of ordinary baryons. Many observational arguments hint at the existence of a second, more exotic species known as cold dark matter (though they do not quite establish its existence unless they are combined with ideas about the formation of large-scale structure). Experiments also imply the existence of a third dark-matter species, the massive neutrino, although its role appears to be more limited. Finally, all these components are dwarfed in importance by a newcomer whose physical origin remains shrouded in obscurity: the dark energy of the vacuum.

In the remainder of this review, we explore the leading candidates for dark energy and matter in more detail: the cosmological vacuum, elementary particles such as axions, neutrinos and weakly-interacting massive particles (WIMPs), and black holes. Our approach is to constrain each proposal by calculating its contributions to the background radiation, and comparing these with observational data at wavelengths ranging from radio waves to -rays. In the spirit of Olbers' paradox and what we have done so far, our main question for each candidate will thus be: Just how dark is it?