5. DARK ENERGY

5.1. The variable cosmological "constant"

The cosmological-constant problem is essentially the problem of reconciling the very high vacuum-energy densities expected on the basis of quantum field theory with the small (but nonzero) dark-energy density now inferred from cosmological observation (Sec. 4.5). Many authors have sought to bridge the gap by looking for a mechanism that would allow the energy density _v of the vacuum to decay with time. Since c² = 8 G _v from (23), this means replacing Einstein's cosmological constant by a variable "cosmological term." With such a mechanism in hand, the problem would be reduced to explaining why the Universe is of intermediate age: old enough that has relaxed from primordial values like those suggested by quantum field theory to the values which we measure now, but young enough that _v / _crit has not yet reached its asymptotic value of unity.

Energy conservation requires that any decrease in the energy density of the vacuum be made up by a corresponding increase somewhere else. In some scenarios, dark energy goes into the kinetic energy of new forms of matter such as scalar fields, which have yet to be observed in nature. In others it is channelled instead into baryons, photons or neutrinos. Baryonic decays would produce equal amounts of matter and antimatter, whose subsequent annihilation would flood the Universe with -rays. Radiative decays would similarly pump photons into intergalactic space, but are harder to constrain because they could in principle involve any part of the electromagnetic spectrum. As we will see, however, robust limits can be set on any such process under conservative assumptions.

But how can , originally introduced by Einstein in 1917 as a constant of nature akin to c and G, be allowed to vary? To answer this, we go back to the field equations of general relativity:

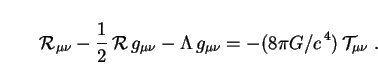(106)

The covariant derivative of these equations can be written in the following form with the help of the Bianchi identities, which read (_µ - 1/2 g_µ) = 0:

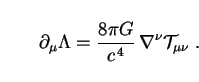(107)

Within Einstein's theory, it follows that = constant as long as matter and energy (as contained in 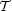_µ) are conserved.

In variable- theories, one must therefore do one of three things: abandon matter-energy conservation, modify general relativity, or stretch the definition of what is conserved. The first of these routes was explored as early as 1933 by Bronstein [145], who sought to connect energy non-conservation with the cosmological arrow of time. Bronstein was executed in Stalin's Soviet Union a few years later, and his work is not widely known [146].

Today, few physicists would be willing to sacrifice energy conservation outright. Some, however, would be willing to modify general relativity, or to consider new forms of matter and energy. Historically, these two approaches have sometimes been seen as distinct, with one being a change to the "geometry of nature" while the other is concerned with the material content of the Universe. The modern tendency, however, is to regard them as equivalent. This viewpoint is best personified by Einstein, who in 1936 compared the left-hand (geometrical) and right-hand (matter) sides of his field equations to "fine marble" and "low-grade wooden" wings of the same house [147]. In a more complete theory, he argued, matter fields of all kinds would be seen to be just as geometrical as the gravitational one.

5.2. Models based on scalar fields

Let us see how this works in one of the oldest and simplest variable- theories: a modification of general relativity in which the metric tensor g_µ is supplemented by a scalar field whose coupling to matter is determined by a parameter . Ideas of this kind go back to Jordan in 1949 [148], Fierz in 1956 [149] and Brans and Dicke in 1961 [150]. In those days, of course, new scalar fields were not bandied about as freely as they are today, and all these authors sought to associate with a known quantity. Various lines of argument (notably Mach's principle) pointed to an identification with Newton's gravitational "constant" such that G ~ 1 / . By 1968 it was appreciated that and too would depend on in general [151]. The original Brans-Dicke theory (with = 0) has subsequently been extended to generalized scalar-tensor theories in which = () [152], = (), = () [153] and = (, ), = () where ^{µ µ} [154]. In the last and most general of these cases, the field equations read

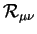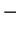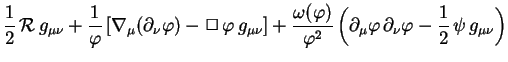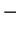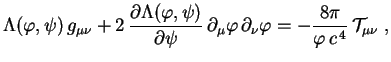			(108)

where ^µ(^µ ) is the D'Alembertian. These reduce to Einstein's equations (106) when = const = 1/G.

If we now repeat the exercise on the previous page and take the covariant derivative of the field equations (108) with the Bianchi identities, we obtain a generalized version of the equation (107) faced by Bronstein:

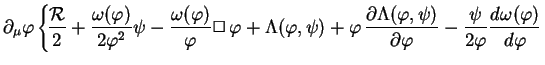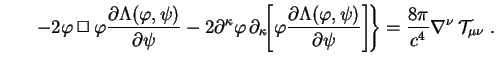	(109)

Now energy conservation ( _µ = 0) no longer requires = const. In fact, it is generally incompatible with constant , unless an extra condition is imposed on the terms inside the curly brackets in (109). (This cannot come from the wave equation for , which merely confirms that the terms inside the curly brackets sum to zero, in agreement with energy conservation.) Similar conclusions hold for other scalar-tensor theories in which is no longer associated with G. Examples include models with non-minimal couplings between and the curvature scalar [155], conformal rescalings of the metric tensor by functions of [156] and nonzero potentials V() [157, 158, 159]. (Theories of this last kind are now known as quintessence models [160]). In each of these scenarios, the cosmological "constant" becomes a dynamical variable.

In the modern approach to variable- cosmology, which goes back to Zeldovich in 1968 [161], all extra terms of the kind just described -- including -- are moved to the right-hand side of the field equations (108), leaving only the Einstein tensor (_µ - 1/2 g_µ) to make up the "geometrical" left-hand side. The cosmological term, along with scalar (or other) additional fields, are thus effectively reinterpreted as new kinds of matter. Eqs. (108) then read

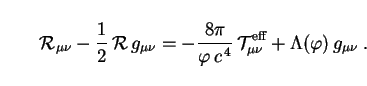(110)

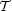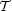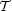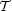
Here ^eff_µ is an effective energy-momentum tensor describing the sum of ordinary matter plus whatever scalar (or other) fields have been added to the theory. For generalized scalar-tensor theories as described above, this could be written as ^eff_{µ µ} + _µ where _µ refers to ordinary matter and 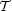_µ to the scalar field. For the case with = () and = (), for instance, the latter would be defined by (108) as

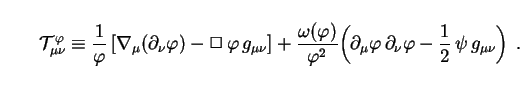(111)

The covariant derivative of the field equations (110) now reads

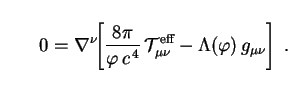(112)

Eq. (112) carries the same physical content as (109), but is more general in form and can readily be extended to other theories. Physically, it says that energy is conserved in variable- cosmology -- where "energy" is now understood to refer to the energy of ordinary matter along with that in any additional fields which may be present, and along with that in the vacuum, as represented by . In general, the latter parameter can vary as it likes, so long as the conservation equation (112) is satisfied.

It was noted at least as early as 1977 by Endo and Fukui [152] that the evolution of in theories of this kind can help with the cosmological "constant" problem, in the sense of dropping from large primordial values to ones like those seen today. These authors found solutions for (t) such that t^-2 when = () and = constant. In precursors to the modern quintessence scenarios, Barr [157] found models in which t^- at late times, while Peebles and Ratra [158] discussed a theory in which R^-m at early ones (here and m are powers). There is now a rich literature on -decay laws of this kind [113]. Their appeal is easy to understand, and can be illustrated with a simple dimensional argument for the case with R^-2 [162]. Since already has dimensions of L^-2, the proportionality factor in this case is a pure number (, say) which is presumably of order unity. Taking ~ 1 and identifying R with a suitable length scale in cosmology (namely the Hubble distance c / H₀), one finds that ₀ ~ H₀² / c². The present vacuum density parameter is then _{,0 0} c² / 3H₀² ~ 1/3, close to the values implied by by the supernovae data (Sec. 4.5). The most natural choice R ~ _Pl gives a primordial -term of _Pl ~ _Pl^-2. It then follows that _Pl / ₀ ~ (c / H_{0 Pl})² ~ 10¹²², in good agreement with the values suggested by Table 3.

5.3. Theoretical and observational challenges

While this would seem to be a promising approach, two cautions must be kept in mind. The first is theoretical. Insofar as the mechanisms discussed so far are entirely classical, they do not address the underlying problem. For this, one would also need to explain why net contributions to from the quantum vacuum do not remain at the primordial level, or how they are suppressed with time. Polyakov [163] and S.L. Adler [164] in 1982 were the first to speculate explicitly that such a suppression might come about if the "bare" cosmological term implied by quantum field theory were progressively screened by an "induced" counterterm of opposite sign, driving the effective value of (t) toward zero at late times. Many theoretical adjustment mechanisms have now been identified as potential sources of such a screening effect, beginning with a 1983 suggestion by Dolgov [165] based on non-minimally coupled scalar fields. Subsequent proposals have involved scalar fields [166, 167, 168], fields of higher spin [169, 170, 171], quantum effects during inflation [172, 173, 174] and other phenomena [175, 176, 177]. In most of these cases, no analytic expression is found for in terms of time or other cosmological parameters; the intent is merely to demonstrate that decay (and preferably near-cancellation) of the cosmological term is possible in principle. None of these mechanisms has been widely accepted as successful to date. In fact, there is a general argument due to Weinberg to the effect that a successful mechanism based on scalar fields would necessarily be so finely-tuned as to be just as mysterious as the original problem [178]. Similar concerns have been raised in the case of vector and tensor-based proposals [179]. Nevertheless, the idea of the adjustment mechanism remains feasible in principle, and continues to attract more attention than any other approach to the cosmological-constant problem.

The second caution is empirical. Observational data place increasingly strong restrictions on the way in which can vary with time. Among the most important are early-time bounds on the dark-energy density c² = c⁴ / 8 G. The success of standard primordial nucleosynthesis theory implies that was smaller than _r and _m during the radiation-dominated era, and large-scale structure formation could not have proceeded in the conventional way unless < _m during the early matter-dominated era. Since _r R^-4 and _m R^-3 from (32), these requirements mean in practice that the dark-energy density must climb less steeply than R^-3 in the past direction, if it is comparable to that of matter or radiation at present [180, 181]. The variable- term must also satisfy late-time bounds like those which have been placed on the cosmological constant (Sec. 4.5). Tests of this kind have been carried out using data on the age of the Universe [182, 183], structure formation [184, 185, 186], galaxy number counts [187], the CMB power spectrum [188, 189], gravitational lensing statistics [189, 190, 191] and Type Ia supernovae [189, 192]. Some of these tests are less restrictive in the case of a variable -term than they are for = const, and this can open up new regions of parameter space. Observation may even be compatible with some nonsingular models whose expansion originates in a hot, dense "big bounce" rather than a big bang [193], a possibility which can be ruled out on general grounds if = constant.

A third group of limits comes from asking what the vacuum decays into. In quintessence theories, dark energy is transferred to the kinetic energy of a scalar field as it "rolls" down a gradient toward the minimum of its potential. This may have observable consequences if the scalar field is coupled strongly to ordinary matter, but is hard to constrain in general. A simpler situation is that in which the vacuum decays into known particles such as baryons, photons or neutrinos. The baryonic decay channel would produce excessive levels of -ray background radiation due to matter-antimatter annihilation unless the energy density of the vacuum component is less than 3 × 10^-5 times that of matter [180]. This limit can be weakened if the decay process violates baryon number, or if it takes place in such a way that matter and antimatter are segregated on large scales, but such conditions are hard to arrange in a natural way. The radiative decay channel is more promising, but also faces a number of tests. The decay process should meet certain criteria of thermodynamic stability [194] and adiabaticity [195]. The shape of the spectrum of decay photons must not differ too much from that of pre-existing background radiation, or distortions will arise. Freese have argued on this basis that the energy density of a vacuum decaying primarily into low-energy photons could not exceed 4 × 10^-4 times that of radiation [180].

It may be, however, that vacuum-decay photons blend into the spectrum of background radiation without distorting it. Fig. 1 shows that the best place to "hide" the evidence of such a process would be the microwave region, where the energy density of background radiation is highest. Could all or part of the CMB be due to dark-energy decay? We know from the COBE satellite that its spectrum is very nearly that of a perfect blackbody [196]. Freese pointed out that vacuum-decay photons would be thermalized efficiently by brehmsstrahlung and double-Compton scattering in the early Universe, and might continue to assume a blackbody spectrum at later times if pre-existing CMB photons played a role in "inducing" the vacuum to decay [180]. Subsequent work has shown that this would require a special combination of thermodynamical parameters [197]. This possibility is important in practice, however, because it leads to the most conservative limits on the theory. Even if the radiation produced by decaying dark energy does not distort the background, it will contribute to the latter's absolute intensity. We can calculate the size of these contributions to the background radiation using the methods that have been laid out in Secs. 2 and 3.

5.4. A phenomenological model

The first step in this problem is to solve the field equations and conservation equations for the energy density of the decaying vacuum. We will do this in the context of a general phenomenological model. This means that we retain the field equations (110) and the conservation law (112) without specifying the form of the effective energy-momentum tensor in terms of scalar (or other) fields. These equations may be written

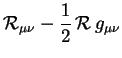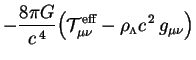			(113)
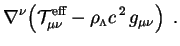			(114)

Here c ² c ⁴ / 8 G from (23) and we have replaced 1 / with G (assumed to be constant in what follows). Eqs. (113) and (114) have the same form as their counterparts (106) and (29) in standard cosmology, the key difference being that the cosmological term has migrated to the right-hand side and is no longer necessarily constant. Its evolution is now governed by the conservation equations (114), which require only that any change in c² g_µ be balanced by an equal and opposite change in the energy-momentum tensor 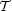^eff_µ.

While the latter is model-dependent in general, it is reasonable to assume in the context of isotropic and homogeneous cosmology that its form is that of a perfect fluid, as given by (26):

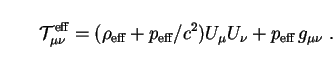(115)

Comparison of Eqs. (114) and (115) shows that the conserved quantity in (114) must then also have the form of a perfect-fluid energy-momentum tensor, with density and pressure given by

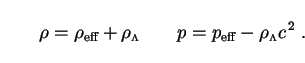(116)

The conservation law (114) may then be simplified at once by analogy with Eq. (29):

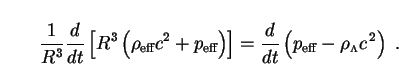(117)

This reduces to the standard result (30) for the case of a constant cosmological term, = const. Throughout Sec. 5, we allow the cosmological term to contain both a constant part and a time-varying part so that

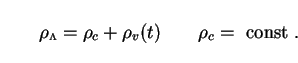(118)

Let us assume in addition that the perfect fluid described by 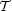^eff_µ consists of a mixture of dust-like matter (p_m = 0) and radiation (p_r = 1/3 _r c ²):

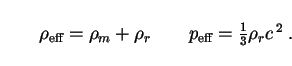(119)

The conservation equation (117) then reduces to

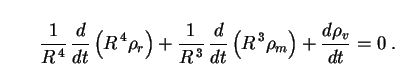(120)

From this equation it is clear that one (or both) of the radiation and matter densities can no longer obey the usual relations _r R^-4 and _m R^-3 in a theory with const. Any change in (or ) must be accompanied by a change in radiation and/or matter densities.

To go further, some simplifying assumptions must be made. Let us take to begin with:

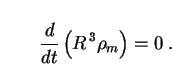(121)

This is just conservation of particle number, as may be seen by replacing "galaxies" with "particles" in Eq. (6). Such an assumption is well justified during the matter-dominated era by the stringent constraints on matter creation discussed in Sec. 5.1. It is equally well justified during the radiation-dominated era, when the matter density is small so that the _m term is of secondary importance compared to the other terms in (120) in any case.

In light of Eqs. (120) and (121), the vacuum can exchange energy only with radiation. As a model for this process, let us follow Pollock in 1980 [198] and assume that it takes place in such a way that the energy density of the decaying vacuum component remains proportional to that of radiation, _{v r}. We adopt the notation of Freese in 1987 and write the proportionality factor as x / (1 - x) with x the coupling parameter of the theory [180]. If this is allowed to take (possibly different) constant values during the radiation and matter-dominated eras, then

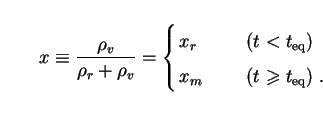(122)

Here t_eq refers to the epoch of matter-radiation equality when _r = _m. Standard cosmology is recovered in the limit x 0. The most natural situation is that in which the value of x stays constant, so that x_r = x_m. However, since observational constraints on x are in general different for the radiation and matter-dominated eras, the most conservative limits on the theory are obtained by letting x_r and x_m take different values. Physically, this would correspond to a phase transition or sudden change in the expansion rate / R of the Universe at t = t_eq.

With Eqs. (121) and (122), the conservation equation (120) reduces to

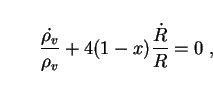(123)

where overdots denote derivatives with respect to time. Integration gives

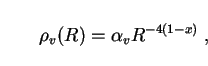(124)

where _v is a constant. The cosmological term is thus an inverse power-law function of the scale factor R, a scenario that has received wide attention also in models where vacuum energy is not proportional to that of radiation [113]. Eq. (124) shows that the conserved quantity in this theory has a form intermediate between that of ordinary radiation entropy (R ⁴_r) and particle number (R ³_m) when 0 < x < 1/4.

The fact that _{r v} R^-4(1-x) places an immediate upper limit of 1/4 on x (in both eras), since higher values would erase the dynamical distinction between radiation and matter. With x 1/4 it then follows from (122) that _v 1/3 _r. This is consistent with Sec. 5.1, where we noted that a vacuum component whose density climbs more steeply than R^-3 in the past direction cannot have an energy density greater than that of radiation at present. Freese [180] set a stronger bound by showing that x 0.07 if the baryon-to-photon ratio is to be consistent with both primordial nucleosynthesis and present-day CMB observations. (This argument assumes that x = x_r = x_m.) As a guideline in what follows, then, we will allow x_r and x_m to take values between zero and 0.07, and consider in addition the theoretical possibility that x_m could increase to 0.25 in the matter-dominated era.

5.5. Energy density

With _m(R) specified by (121), _r related to _v by (122) and _v(R) given by (124), we can solve for all three components as functions of time if the scale factor R(t) is known. This comes as usual from the field equations (113). Since these are the same as Eqs. (106) for standard cosmology, they lead to the same result, Eq. (22):

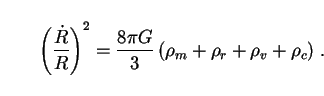(125)

Here we have used Eqs. (118) to replace with _v + _c and (119) to replace _eff with _m + _r. We have also set k = 0 since observations indicate that these components together make up very nearly the critical density (Sec. 4).

Eq. (125) can be solved analytically in the three cases which are of greatest physical interest: (1) the radiation-dominated regime, for which t < t_eq and _r + _v >> _m + _c; (2) the matter-dominated regime, which has t t_eq and _r + _v << _m (if _c = 0); and (3) the vacuum-dominated regime, for which t t_eq and _r + _v << _m + _c. The distinction between regimes 2 and 3 allows us to model both matter-only universes like EdS and vacuum-dominated cosmologies like CDM or BDM (Table 2). The definitions of these terms should be amended slightly for this section, since we now consider flat models containing not only matter and a cosmological constant, but radiation and a decaying-vacuum component as well. The densities of the latter two components are, however, at least four orders of magnitude below that of matter at present. Thus models with _c = 0, for example, have _m,0 = 1 to four-figure precision or better and are dynamically indistinguishable from EdS during all but the first fraction (of order 10^-4 or less) of their lifetimes. For definiteness, we will use the terms "EdS," "CDM" and "BDM" in this section to refer to flat models in which _m,0 = 1, 0.3 and 0.03 respectively. In all cases, the present dark-energy density (if any) comes almost entirely from its constant-density component.

Eqs. (121), (122), (124) and (125) can be solved analytically for R, _m, _r and _v in terms of R ₀, _m,0, _r,0, x_r and x_m (see [1] for details). The normalized scale factor is found to read

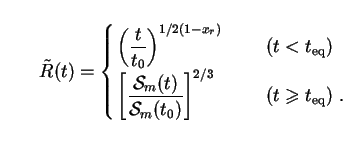(126)

The dark-energy density is given by

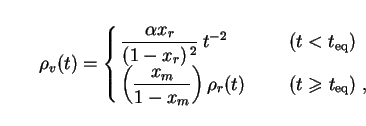(127)

where = 3/(32 G) = 4.47 × 10⁵ g cm^-2 s². The densities of radiation and matter are

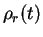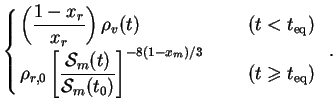			(128)

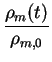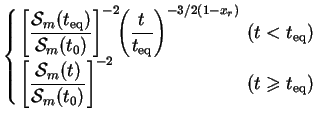Here we have applied _m,0 = _{m,0 crit,0} and _r,0 = _{r,0 crit,0} as boundary conditions. The function 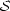_m(t) is defined as

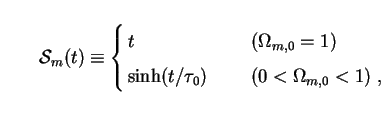(129)

where ₀ 2 / [3H₀ (1 - _m,0)^1/2]. The age of of the Universe is

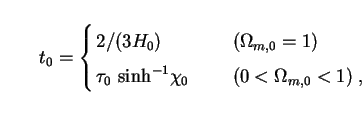(130)

where ₀ [(1 - _m,0) / _m,0]^1/2 and we have used Eq. (56). Corrections from the radiation-dominated era can be ignored since t₀ >> t_eq in all cases.

The parameter t_eq is obtained as in standard cosmology by setting _r (t_eq) = _m (t_eq) in Eqs. (128). This leads to

(131)

The epoch of matter-radiation equality plays a crucial role because it is at about this time that the Universe became transparent to radiation (the two events are not simultaneous but the difference between them is minor for our purposes). Decay photons created before t_eq would simply have been thermalized by the primordial plasma and eventually re-emitted as part of the CMB. It is the decay photons emitted after this time which can contribute to the extragalactic background radiation, and whose contributions we wish to calculate. The quantity t_eq is thus analogous to the galaxy formation time t_f in previous sections.

The densities _m(t), _r(t) and _v(t) are plotted as functions of time in Fig. 22. The left-hand panel (a) shows the effects of varying the parameters x_r and x_m within a given cosmological model (here, CDM). Raising the value of x_m leads to a proportionate increase in _v and a modest drop in _r. It also flattens the slope of both components. The change in slope (relative to that of the matter component) pushes the epoch of equality back toward the big bang (vertical lines). Such an effect could in principle allow more time for structure to form during the early matter-dominated era [180], although the "compression" of the radiation-dominated era rapidly becomes unrealistic for values of x_m close to 1/4. Thus Fig. 22(a) shows that the value of t_eq is reduced by a factor of over 100 in going from a model with x_m = 10^-4 to one with x_m = 0.07. In the limit x_m 1/4, the radiation-dominated era disappears altogether, as remarked above and as shown explicitly by Eqs. (131).

Figure 22. The densities of decaying dark energy (v, radiation (r) and matter (m) as functions of time. Panel (a) shows the effects of changing the values of xr and xm, assuming a model with m,0 = 0.3 (similar to CDM). Panel (b) shows the effects of changing the cosmological model, assuming xr = xm = 10-4. The vertical lines indicate the epochs when the densities of matter and radition are equal (teq). All curves assume h0 = 0.75.

Fig. 22(b) shows the effects of changes in cosmological model for fixed values of x_r and x_m (here both set to 10^-4). Moving from the matter-filled EdS model toward vacuum-dominated ones such as CDM and BDM does three things. The first is to increase the age (t₀) of the Universe. This increases the density of radiation at any given time, since the latter is fixed at present and climbs at the same rate in the past direction. Based on our experience with the galactic EBL in previous sections, we may expect that this should lead to significantly higher levels of background radiation when integrated over time. However, there is a second effect in the present theory which acts in the opposite direction: smaller values of _m,0 boost the value of t_eq as well as t₀, thus delaying the onset of the matter-dominated era (vertical lines). As we will see, these two changes all but cancel each other out as far as dark-energy contributions to the background are concerned. The third consequence of vacuum-dominated cosmologies is "late-time inflation," the sharp increase in the expansion rate at recent times (Fig. 18). This translates in Fig. 22(b) into the drop-off in the densities of all three components at the right-hand edge of the figure for the CDM and BDM models.

5.6. Source luminosity

In order to make use of the formalism we have developed in Secs. 2 and 3, we need to define discrete "sources" of radiation from dark-energy decay, analogous to the galaxies of previous sections. For this purpose we carve up the Universe into hypothetical regions of arbitrary comoving volume V₀. The comoving number density of these source regions is just

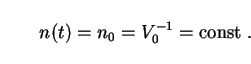(132)

These regions are introduced for convenience, and are not physically significant since dark energy decays uniformly throughout space. We therefore expect that the parameter V₀ will not appear in our final results.

The next step is to identify the "source luminosity." There are at least two ways to approach this question [199]. One could simply regard the source region as a ball of physical volume V(t) = 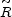³(t) V₀ filled with fluctuating dark energy. As the density of this energy drops by - d_v during time dt, the ball loses energy at a rate - d_v / dt. If some fraction of this energy flux goes into photons, then the luminosity of the ball is

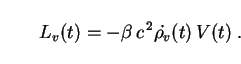(133)

This is the definition of vacuum luminosity which has been assumed implicitly by workers such as Pavón [194], who investigated the thermodynamical stability of the vacuum decay process by requiring that fluctuations in 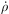_v not grow larger than the mean value of 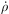_v with time. For convenience we will refer to (133) as the thermodynamical definition of vacuum luminosity (L_th).

A second approach is to treat this as a problem involving spherical symmetry within general relativity. The assumption of spherical symmetry allows the total mass-energy (Mc ²) of a localized region of perfect fluid to be identified unambiguously. Luminosity can then be related to the time rate of change of this mass-energy. Assuming once again that the two are related by a factor , one has

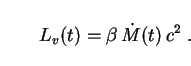(134)

Application of Einstein's field equations leads to the following expression [201] for the rate of change of mass-energy in terms of the pressure p_v at the region's surface:

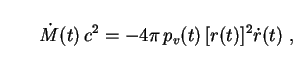(135)

where r(t) = (t) r₀ is the region's physical radius. Taking V = 4/3 r³, applying the vacuum equation of state p_v = - _v c ² and substituting (135) into (134), we find that the latter can be written in the form

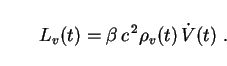(136)

This is just as appealing dimensionally as Eq. (133), and shifts the emphasis physically from fluctuations in the material content of the source region toward changes in its geometry. We will refer to (136) for convenience as the relativistic definition of vacuum luminosity (L_rel).

It is not obvious which of the two definitions (133) and (136) more correctly describes the luminosity of decaying dark energy; this is a conceptual issue. Before choosing between them, let us inquire whether the two expressions might not be equivalent. We can do this by taking the ratio

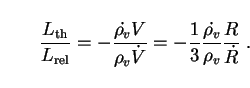(137)

Differentiating Eqs. (126) and (127) with respect to time, we find

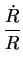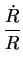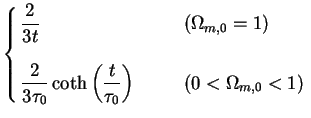			(138)
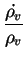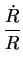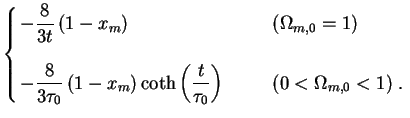			(139)

The ratio L_th / L_rel is therefore constant [= 4(1 - x_m) / 3], taking values between 4/3 (in the limit x_m 0 where standard cosmology is recovered) and 1 (in the opposite limit where x_m takes its maximum theoretical value of 1/4). There is thus little difference between the two scenarios in practice, at least where this model of decaying dark energy is concerned. We will proceed using the relativistic definition (136) which gives lower intensities and hence more conservative limits on the theory. At the end of the section it will be a small matter to calculate the corresponding intensity for the thermodynamical case (133) by multiplying through by 4/3 (1 - x_m).

We now turn to the question of the branching ratio , or fraction of decaying dark energy which goes into photons as opposed to other forms of radiation such as massless neutrinos. This is model-dependent in general. If the vacuum-decay radiation reaches equilibrium with that already present, however, then we may reasonably set this equal to the ratio of photon-to-total radiation energy densities in the CMB:

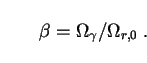(140)

The density parameter of CMB photons is given in terms of their blackbody temperature T by Stefan's law. Using the COBE value T_cmb = 2.728 K [196], we get

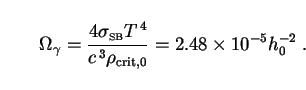(141)

The total radiation density _r,0 = + is harder to determine, since there is little prospect of detecting the neutrino component directly. What is done in standard cosmology is to calculate the size of neutrino contributions to _r,0 under the assumption of entropy conservation. With three light neutrino species, this leads to

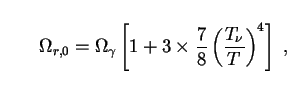(142)

where T is the blackbody temperature of the relic neutrinos and the factor of 7/8 arises from the fact that these particles obey Fermi rather than Bose-Einstein statistics [200]. During the early stages of the radiation-dominated era, neutrinos were in thermal equilibrium with photons so that T = T. They dropped out of equilibrium, however, when the temperature of the expanding fireball dropped below about kT ~ 1 MeV (the energy scale of weak interactions). Shortly thereafter, when the temperature dropped to kT ~ m_e c² = 0.5 MeV, electrons and positrons began to annihilate, transferring their entropy to the remaining photons in the plasma. This raised the photon temperature by a factor of (1 + 2 × 7/8 = 11/4)^1/3 relative to that of the neutrinos. In standard cosmology, the ratio of T / T has remained at (4/11)^1/3 down to the present day, so that (142) gives

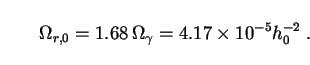(143)

Using (140) for , this would imply:

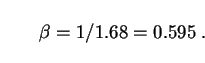(144)

We will take these as our "standard values" of _r,0 and in what follows. They are conservative ones, in the sense that most alternative lines of argument would imply higher values of . Birkel and Sarkar [181], for instance, have argued that vacuum decay (with a constant value of x_r) would be easier to reconcile with processes such as electron-positron annihilation if the vacuum coupled to photons but not neutrinos. This would complicate the theory, breaking the radiation density _r in (120) into a photon part and a neutrino part with different dependencies on R. One need not solve this equation, however, in order to appreciate the main impact that such a modification would have. Decay into photons alone would pump entropy into the photon component relative to the neutrino component in an effectively ongoing version of the electron-positron annihilation argument described above. The neutrino temperature T (and density ) would continue to be driven down relative to T (and ) throughout the radiation-dominated era and into the matter-dominated one. In the limit T / T 0 one sees from (140) and (142) that such a scenario would lead to

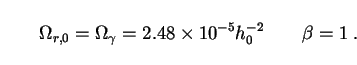(145)

In other words, the present energy density of radiation would be lower, but it would effectively all be in the form of photons. Insofar as the decrease in _r,0 is precisely offset by the increase in , these changes cancel each other out. The drop in _r,0, however, has an added consequence which is not cancelled: it pushes t_eq farther into the past, increasing the length of time over which decaying dark energy has been contributing to the background. This raises the latter's intensity, particularly at longer wavelengths. The effect can be significant, and we will return to this possibility at the end of the section. For the most part, however, we will stay with the values of _r,0 and given by Eqs. (143) and (144).

Armed with a definition for vacuum luminosity, Eq. (136), and a value for , Eq. (144), we are in a position to calculate the luminosity of decaying dark energy. Noting that 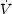= 3(R / R₀)³ (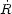 / R) V₀ and substituting Eqs. (127) and (138) into (136), we find that

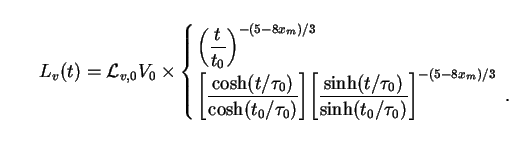(146)

The first of these solutions corresponds to models with _m,0 = 1 while the the second holds for the general case (0 < _m,0 < 1). Both results reduce at the present time t = t₀ to

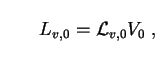(147)

where _{v, 0} is the comoving luminosity density of decaying dark energy

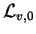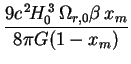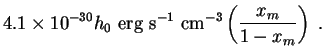			(148)

Numerically, we find for example that

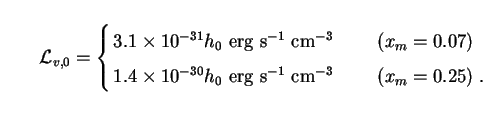(149)

In principle, dark-energy decay can produce a background 10 or even 50 times more luminous than that of galaxies, as given by (20). Raising the value of the branching ratio to 1 instead of 0.595 does not affect these results, since this must be accompanied by a proportionate drop in the value of _r,0 as argued above. The numbers in (149) do go up if one replaces the relativistic definition (136) of vacuum luminosity with the thermodynamical one (133) but the change is modest, raising _{v, 0} by no more than a factor of 1.2 (for x_m = 0.07). The primary reason for the high luminosity of the decaying vacuum lies in the fact that it converts nearly 60% of its energy density into photons. By comparison, less than 1% of the rest energy of ordinary luminous matter has gone into photons so far in the history of the Universe.

5.7. Bolometric intensity

We showed in Sec. 2 that the bolometric intensity of an arbitrary distribution of sources with comoving number density n(t) and luminosity L(t) could be expressed as an integral over time by (12). Let us apply this result here to regions of decaying dark energy, for which n_v(t) and L_v(t) are given by (132) and (146) respectively. Putting these equations into (12) along with (126) for the scale factor, we find that

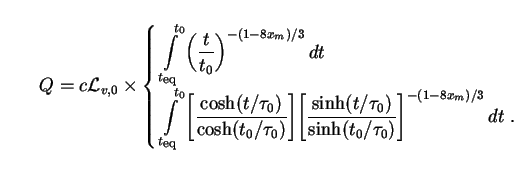(150)

The first of these integrals corresponds to models with _m,0 = 1 while the second holds for the general case (0 < _m,0 < 1). The latter may be simplified with a change of variables to y [sinh(t / ₀)]^8x_m/3. Using the facts that sinh(t₀ / ₀) = [(1 - _m,0) / _m,0]^1/2 and cosh(t₀ / ₀) = 1 / [_m,0]^1/2 along with the definition (131) of t_eq, both integrals reduce to the same formula:

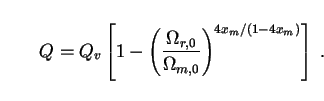(151)

Here Q_v is found with the help of (148) as

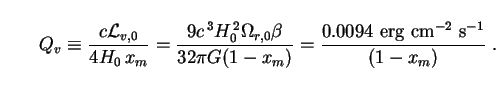(152)

There are several points to note about this result. First, it does not depend on V₀, as expected. There is also no dependence on the uncertainty h₀ in Hubble's constant, since the two factors of h₀ in H₀ ² are cancelled out by those in _r,0. In the limit x_m 0 one sees that Q 0 as expected. In the opposite limit where x_m 1/4, decaying dark energy attains a maximum possible bolometric intensity of Q Q_v = 0.013 erg cm^-2 s^-1. This is 50 times the bolometric intensity due to galaxies, as given by (21).

The matter density _m,0 enters only weakly into this result, and plays no role at all in the limit x_m 1/4. Based on our experience with the EBL due to galaxies, we might have expected that Q would rise significantly in models with smaller values of _m,0 since these have longer ages, giving more time for the Universe to fill up with light. What is happening here, however, is that the larger values of t₀ are offset by larger values of t_eq (which follow from the fact that smaller values of _m,0 imply smaller ratios of _m,0 / _r,0). This removes contributions from the early matter-dominated era and thereby reduces the value of Q. In the limit x_m 1/4 these two effects cancel each other out. For smaller values of x_m, the t_eq-effect proves to be the stronger of the two, and one finds an overall decrease in Q for these cases. With x_m = 0.07, for instance, the value of Q drops by 2% when moving from the EdS model to CDM, and by another 6% when moving from CDM to BDM.

5.8. Spectral energy distribution

To obtain limits on the parameter x_m, we would like to calculate the spectral intensity of the background due to dark-energy decay, just as we did for galaxies in Sec. 3. For this we need to know the spectral energy distribution (SED) of the decay photons. As discussed in Sec. 5.1, theories in which the these photons are distributed with a non-thermal spectrum can be strongly constrained by means of distortions in the CMB. We therefore restrict ourselves to the case of a blackbody SED, as given by Eq. (78):

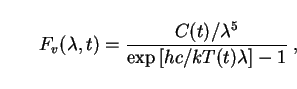(153)

where T(t) is the blackbody temperature. The function C(t) is found as usual by normalization, Eq. (57). Changing integration variables from to = c / , we find

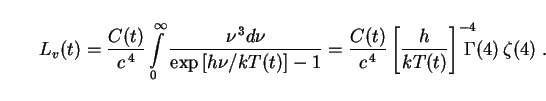(154)

Inserting our result (146) for L_v(t) and using the facts that (4) = 3! = 6 and (4) = ⁴ / 90, we then obtain for C(t):

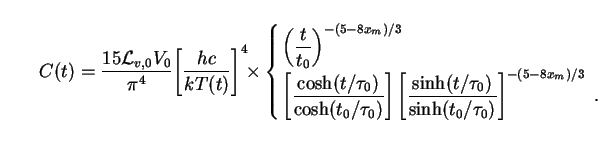(155)

Here the upper expression refers as usual to the EdS case (_m,0 = 1), while the lower applies to the general case (0 < _m,0 < 1). The temperature of the photons can be specified if we assume thermal equilibrium between those created by vacuum decay and those already present. Stefan's law then relates T(t) to the radiation energy density _r (t) c ² as follows:

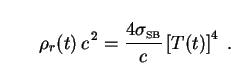(156)

Putting Eq. (128) into this expression and expanding the Stefan-Boltzmann constant, we find that

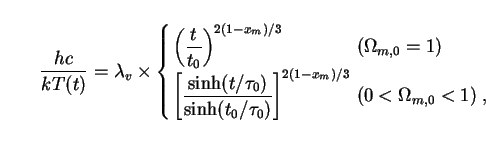(157)

where the constant _v is given by

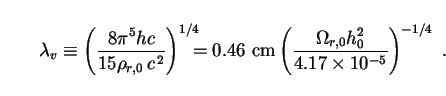(158)

This value of _v tells us that the peak of the observed spectrum of decay radiation lies in the microwave region as expected, near that of the CMB (_cmb = 0.11 cm). Putting (157) back into (155), we obtain

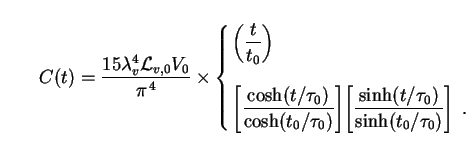(159)

These two expressions refer to models with _m,0 = 1 and 0 < _m,0 < 1 respectively. This specifies the SED (153) of decaying dark energy.

5.9. The microwave background

The spectral intensity of an arbitrary distribution of sources with comoving number density n(t) and an SED F(, t) is expressed as an integral over time by Eq. (61). Putting Eqs. (126), (132) and (153) into this equation, we obtain

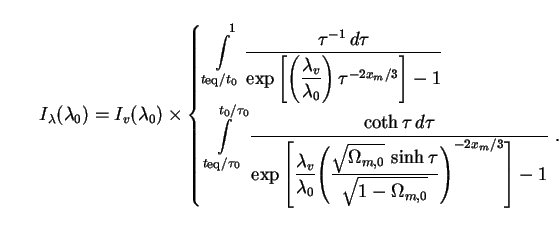(160)

Here we have used integration variables t / t₀ in the first case (_m,0 = 1) and t / ₀ in the second (0 < _m,0 < 1). The dimensional content of both integrals is contained in the prefactor I_v(₀), which reads

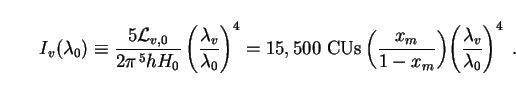(161)

We have divided this quantity through by photon energy hc / ₀ so as to express the results in continuum units (CUs) as usual, where 1 CU 1 photon s^-1 cm^-2 Å^-1 ster^-1. We use CUs throughout this review, for the sake of uniformity as well as the fact that these units carry several advantages from the theoretical point of view (Sec. 3.2). The reader who consults the literature, however, will soon find that each part of the electromagnetic spectrum has its own "dialect" of preferred units. In the microwave region intensities are commonly reported in terms of I, the integral of flux per unit frequency over frequency, and usually expressed in units of nW m^-2 ster^-1 = 10^-6 erg s^-1 cm^-2 ster^-1. To translate a given value of I (in these units) into CUs, one need only multiply by a factor of 10^-6 / (hc) = 50.34 erg^-1 Å^-1. The Jansky (Jy) is also often encountered, with 1 Jy = 10^-23 erg s^-1 cm^-2 Hz^-1. To convert a given value of I from Jy ster^-1 into CUs, one multiplies by a factor of 10^-23 / h = (1509 Hz erg^-1) / with in Å.

Eq. (160) gives the combined intensity of decay photons which have been emitted at many wavelengths and redshifted by various amounts, but reach us in a waveband centered on ₀. The arbitrary volume V₀ has dropped out of the integral as expected, and this result is also independent of the uncertainty h₀ in Hubble's constant since there is a factor of h₀ in both _{v, 0} and H₀. Results are plotted in Fig. 23 over the waveband 0.01-1 cm, together with existing observational data in this part of the spectrum. The most celebrated of these is the COBE detection of the CMB [196] which we have shown as a heavy solid line (F96). The experimental uncertainties in this measurement are far smaller than the thickness of the line. The other observational limits shown in Fig. 23 have been obtained in the far infrared (FIR) region, also from analysis of data from the COBE satellite. These are indicated with heavy dotted lines (F98 [202]) and open triangles (H98 [27] and L00 [203]).

Figure 23. The spectral intensity of background radiation due to the decaying vacuum for various values of xm, compared with observational data in the microwave region (heavy solid line) and far infrared (heavy dotted line and squares). For each value of xm there are three curves representing cosmologies with m,0 = 1 (heaviest lines), m,0 = 0.3 (medium-weight lines) and m,0 = 0.03 (lightest lines). Panel (a) assumes L = Lrel and = 0.595, while panel (b) assumes L = Lth and = 1.

Fig. 23(a) shows the spectral intensity of background radiation from vacuum decay under our standard assumptions, including the relativistic definition (136) of vacuum luminosity and the values of _r,0 and given by (143) and (144) respectively. Five groups of curves are shown, corresponding to values of x_m between 3 × 10^-5 and the theoretical maximum of 0.25. For each value of x_m three curves are plotted: one each for the EdS, CDM and BDM cosmologies. As noted above in connection with the bolometric intensity Q, the choice of cosmological model is less important in determining the background due to vacuum decay than the background due to galaxies. In fact, the intensities here are actually slightly lower in vacuum-dominated models. The reason for this, as before, is that these models have smaller values of _m,0 / _r,0 and hence larger values of t_eq, reducing the size of contributions from the early matter-dominated era when L_v was large.

In Fig. 23(b), we have exchanged the relativistic definition of vacuum luminosity for the thermodynamical one (133), and set = 1 instead of 0.595. As discussed in Sec. 5.6, the increase in is partly offset by a drop in _r,0. There is a net increase in intensity, however, because smaller values of _r,0 push t_eq back into the past, leading to additional contributions from the early matter-dominated era. These contributions particularly push up the long-wavelength part of the spectrum in Fig. 23(b) relative to Fig. 23(a), as seen most clearly in the case x_m = 0.25. Overall, intensities in Fig. 23(b) are higher than those in Fig. 23(a) by about a factor of four.

These figures show that the decaying-vacuum hypothesis is strongly constrained by observations of the microwave background. The parameter x_m cannot be larger than 0.06 or the intensity of the decaying vacuum would exceed that of the CMB itself under the most conservative assumptions, as represented by Fig. 23(a). This limit tightens to x_m 0.015 if different assumptions are made about the luminosity of the vacuum, as shown by Fig. 23(b). These numbers are comparable to the limit of x 0.07 obtained from entropy conservation under the assumption that x = x_r = x_m [180]. And insofar as the CMB is usually attributed entirely to relic radiation from the big bang, the real limit on x_m is probably several orders of magnitude smaller than this.

With these upper bounds on x_m, we can finally inquire about the potential of the decaying vacuum as a dark-energy candidate. Since its density is given by (122) as a fraction x / (1 - x) of that of radiation, we infer that its present density parameter (_v,0) satisfies:

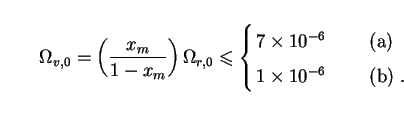(162)

Here, (a) and (b) refer to the scenarios represented by Figs. 23(a) and 23(b), with the corresponding values of _r,0 as defined by Eqs. (143) and (145) respectively. We have assumed that h₀ 0.6 as usual. It is clear from the limits (162) that a decaying vacuum of the kind we have considered here does not contribute significantly to the density of the dark energy.

It should be recalled, however, that there are good reasons from quantum theory for expecting some kind of instability for the vacuum in a universe which progressively cools. (Equivalently, there are good reasons for believing that the cosmological "constant" is not.) Our conclusion is that if the vacuum decays, it either does so very slowly, or in a manner that does not upset the isotropy of the cosmic microwave background.