

Gravity pulls. Newton's Principia generalized this longstanding fact of human experience into a universal attractive force, providing compelling explanations of an extraordinary range of terrestrial and celestial phenomena. Newtonian attraction weakens with distance, but it never vanishes, and it never changes sign. Einstein's theory of General Relativity (GR) reproduces Newtonian gravity in the limit of weak spacetime curvature and low velocities. For a homogeneous universe filled with matter or radiation, GR predicts that the cosmic expansion will slow down over time, in accord with Newtonian intuition. In the late 1990s, however, two independent studies of distant supernovae found that the expansion of the universe has accelerated over the last five billion years (Riess et al. 1998, Perlmutter et al. 1999), a remarkable discovery that is now buttressed by multiple lines of independent evidence. On the scale of the cosmos, gravity repels.
Cosmic acceleration is the most profound puzzle in contemporary physics. Even the least exotic explanations demand the existence of a pervasive new component of the universe with unusual physical properties that lead to repulsive gravity. Alternatively, acceleration could be a sign that GR itself breaks down on cosmological scales. Cosmic acceleration may be the crucial empirical clue that leads to understanding the interaction between gravity and the quantum vacuum, or reveals the existence of extra spatial dimensions, or sheds light on the nature of quantum gravity itself.
Because of these profound implications, cosmic acceleration has inspired a wide range of ambitious experimental efforts, which aim to measure the expansion history and growth of structure in the cosmos with percent-level precision or better. In this article, we review the observational methods that underlie these efforts, with particular attention to techniques that are likely to see major advances over the next decade. We will emphasize the value of a balanced program that pursues several of these methods in combination, both to cross-check systematic uncertainties and to take advantage of complementary information.
The remainder of this introduction briefly recaps the history of cosmic acceleration and current theories for its origin, then sets this article in the context of future experimental efforts and other reviews of the field. Section 2 describes the basic observables that can be used to probe cosmic acceleration, relates them to the underlying equations that govern the expansion history and the growth of structure, and introduces some of the parameters commonly used to define "generic" cosmic acceleration models. It concludes with an overview of the leading methods for measuring these observables. In Sections 3-6 we go through the four most well developed methods in detail: Type Ia supernovae, baryon acoustic oscillations (BAO), weak gravitational lensing, and clusters of galaxies. Section 7 summarizes several other potential probes, whose prospects are currently more difficult to assess but in some cases appear quite promising. Informed by the discussions in these sections, Section 8 presents our principal new results: forecasts of the constraints on cosmic acceleration models that could be achieved by combining results from these methods, based on ambitious but feasible experiments like the ones endorsed by the Astro2010 Decadal Survey report, New Worlds, New Horizons in Astronomy and Astrophysics. We summarize the implications of our analyses in Section 9 .
Just two years after the completion of General Relativity, Einstein (1917) introduced the first modern cosmological model. With little observational guidance, Einstein assumed (correctly) that the universe is homogeneous on large scales, and he proposed a matter-filled space with finite, positively curved, 3-sphere geometry. He also assumed (incorrectly) that the universe is static. Finding these two assumptions to be incompatible, Einstein modified the GR field equation to include the infamous "cosmological term," now usually known as the "cosmological constant" and denoted Λ. In effect, he added a new component whose repulsive gravity could balance the attractive gravity of the matter (though he did not describe his modification in these terms). In the 1920s, Friedman (1922, 1924) and Lemantre (1927) introduced GR-based cosmological models with an expanding or contracting universe, some of them including a cosmological constant, others not. In 1929, Hubble discovered direct evidence for the expansion of the universe (Hubble 1929) thus removing the original motivation for the Λ term. 1 In 1965, the discovery and interpretation of the cosmic microwave background (CMB; Penzias and Wilson 1965, Dicke et al. 1965) provided the pivotal evidence for a hot big bang origin of the cosmos.
From the 1930s through the 1980s, a cosmological constant seemed unnecessary to explaining cosmological observations. The "cosmological constant problem" as it was defined in the 1980s was a theoretical one: why was the gravitational impact of the quantum vacuum vanishingly small compared to the "naturally" expected value (see Section 1.2)? In the late 1980s and early 1990s, however, a variety of indirect evidence began to accumulate in favor of a cosmological constant. Studies of large scale galaxy clustering, interpreted in the framework of cold dark matter (CDM) models with inflationary initial conditions, implied a low matter density parameter Ωm = ρm / ρcrit ≈ 0.15-0.4 (e.g., Maddox et al. 1990, Efstathiou et al. 1990), in agreement with direct dynamical estimates that assumed galaxies to be fair tracers of the mass distribution. Reconciling this result with the standard inflationary cosmology prediction of a spatially flat universe (Guth 1981) required a new energy component with density parameter 1 - Ωm. Open-universe inflation models were also considered, but explaining the observed homogeneity of the CMB (Smoot et al. 1992) in such models required speculative appeals to quantum gravity effects (e.g., Bucher et al. 1995) rather than the semi-classical explanation of traditional inflation.
By the mid-1990s, many cosmological simulation studies included both open-CDM models and Λ-CDM models, along with Ωm = 1 models incorporating tilted inflationary spectra, non-standard radiation components, or massive neutrino components (e.g., Ostriker and Cen 1996, Cole et al. 1997, Gross et al. 1998, Jenkins et al. 1998). Once normalized to the observed level of CMB anisotropies, the large-scale structure predictions of open and flat-Λ models differed at the tens-of-percent level, with flat models generally yielding a more natural fit to the observations (e.g., Cole et al. 1997). Conflict between high values of the Hubble constant and the ages of globular clusters also favored a cosmological constant (e.g., Pierce et al. 1994, Freedman et al. 1994, Chaboyer et al. 1996), though the frequency of gravitational lenses pointed in the opposite direction (Kochanek 1996). Thus, the combination of CMB data, large-scale structure data, age of the universe, and inflationary theory led many cosmologists to consider models with a cosmological constant, and some to declare it as the preferred solution (e.g., Efstathiou et al. 1990, Krauss and Turner 1995, Ostriker and Steinhardt 1995).
Enter the supernovae. In the mid-1990s, two teams set out to measure the cosmic deceleration rate, and thereby determine the matter density parameter Ωm, by discovering and monitoring high-redshift, Type Ia supernovae. The recognition that the peak luminosity of supernovae was tightly correlated with the shape of the light curve (Phillips 1993, Riess et al. 1996) played a critical role in this strategy, reducing the intrinsic distance error per supernova to ~ 10%. While the first analysis of a small sample indicated deceleration (Perlmutter et al. 1997), by 1998 the two teams had converged on a remarkable result: when compared to local Type Ia supernovae (Hamuy et al. 1996), the supernovae at z ≈ 0.5 were fainter than expected in a matter-dominated universe with Ωm ≈ 0.2 by about 0.2 mag, or 20% (Riess et al. 1998, Perlmutter et al. 1999). Even an empty, freely expanding universe was inconsistent with the observations. Both teams interpreted their measurements as evidence for an accelerating universe with a cosmological constant, consistent with a flat universe (Ωtot = 1) having ΩΛ ≈ 0.7.
Why was the supernova evidence for cosmic acceleration accepted so quickly by the community at large? First, the internal checks carried out by the two teams, and the agreement of their conclusions despite independent observations and many differences of methodology, seemed to rule out many forms of observational systematics, even relatively subtle effects of photometric calibration or selection bias. Second, the ground had been well prepared by the CMB and large scale structure data, which already provided substantial indirect evidence for a cosmological constant. This confluence of arguments favored the cosmological interpretation of the results over astrophysical explanations such as evolution of the supernova population or grey dust extinction that increased towards higher redshifts. Third, the supernova results were followed within a year by the results of balloon-borne CMB experiments that mapped the first acoustic peak and measured its angular location, providing strong evidence for spatial flatness (de Bernardis et al. 2000, Hanany et al. 2000; see Netterfield et al. 1997 for earlier ground-based measurements hinting at the same result). On its own, the acoustic peak only implied Ωtot ≈ 1, not a non-zero ΩΛ, but it dovetailed perfectly with the estimates of Ωm and ΩΛ from large scale structure and supernovae. Furthermore, the acoustic peak measurement implied that the alternative to Λ was not an open universe but a strongly decelerating, Ωm = 1 universe that disagreed with the supernova data by 0.5 magnitudes, a level much harder to explain with observational or astrophysical effects. Finally, the combination of spatial flatness and improving measurements of the Hubble constant (e.g., H0 = 71 ± 6 km s-1 Mpc-1; Mould et al. 2000) provided an entirely independent argument for an energetically dominant accelerating component: a matter-dominated universe with Ωtot = 1 would have age t0 = (2/3) H0-1 ≈ 9.5 Gyr, too young to accommodate the 12-14 Gyr ages estimated for globular clusters (e.g., Chaboyer 1998).
A decade later, the web of observational evidence for cosmic acceleration is intricate and robust. A wide range of observations — including larger and better calibrated supernova samples over a broader redshift span, high-precision CMB data down to small angular scales, the baryon acoustic scale in galaxy clustering, weak lensing measurements of dark matter clustering, the abundance of massive clusters in X-ray and optical surveys, the level of structure in the Lyα forest, and precise measurements of H0 — are all consistent with an inflationary cold dark matter model with a cosmological constant, commonly abbreviated as ΛCDM. 2 Explaining all of these data simultaneously requires an accelerating universe. Completely eliminating any one class of constraints (e.g., supernovae, or CMB, or H0) would not change this conclusion, nor would doubling the estimated systematic errors on all of them. The question is no longer whether the universe is accelerating, but why.
1.2. Theories of Cosmic Acceleration
A cosmological constant is the mathematically simplest solution to the cosmic acceleration puzzle. While Einstein introduced his cosmological term as a modification to the curvature side of the field equation, it is now more common to interpret Λ as a new energy component, constant in space and time. For an ideal fluid with energy density u and pressure p, the effective gravitational source term in GR is (u + 3p) / c2, reducing to the usual mass density ρ = u / c2 if the fluid is non-relativistic. For a component whose energy density remains constant as the universe expands, the first law of thermodynamics implies that when a comoving volume element in the universe expands by a (physical) amount dV, the corresponding change in energy is related to the pressure via -p dV = dU = udV. Thus, p = -u, making the gravitational source term (u + 3p) / c2 = -2u / c2. A form of energy that is constant in space and time must have a repulsive gravitational effect.
According to quantum field theory, "empty" space is filled with a sea of virtual particles. It would be reasonable to interpret the cosmological constant as the gravitational signature of this quantum vacuum energy, much as the Lamb shift is a signature of its electromagnetic effects. 3 The problem is one of magnitude. Since virtual particles of any allowable mass can come into existence for short periods of time, the "natural" value for the quantum vacuum density is one Planck Mass per cubic Planck Length. This density is about 120 orders of magnitude larger than the cosmological constant suggested by observations: it would drive accelerated expansion with a timescale of tPlanck ≈ 10-43 sec instead of tHubble ≈ 1018 sec. Since the only "natural" number close to 10-120 is zero, it was generally assumed (prior to 1990) that a correct calculation of the quantum vacuum energy would eventually show it to be zero, or at least suppressed by an extremely large exponential factor (see review by Weinberg 1989). But the discovery of cosmic acceleration raises the possibility that the quantum vacuum really does act as a cosmological constant, and that its energy scale is 10-3 eV rather than 1028 eV for reasons that we do not yet understand. To date, there are no compelling theoretical arguments that explain either why the fundamental quantum vacuum energy might have this magnitude or why it might be zero.
The other basic puzzle concerning a cosmological constant is: Why now? The ratio of a constant vacuum energy density to the matter density scales as a3(t), so it has changed by a factor of ~ 1027 since big bang nucleosynthesis and by a factor ~ 1042 since the electroweak symmetry breaking epoch, which seems (based on our current understanding of physics) like the last opportunity for a major rebalancing of matter and energy components. It therefore seems remarkably coincidental for the vacuum energy density and the matter energy density to have the same order of magnitude today. In the late 1970s, Robert Dicke used a similar line of reasoning to argue for a spatially flat universe (see Dicke and Peebles 1979), an argument that provided much of the initial motivation for inflationary theory (Guth 1981). However, while the universe appears to be impressively close to spatial flatness, the existence of two energy components with different a(t) scalings means that Dicke's "coincidence problem" is still with us.
One possible solution to the coincidence problem is anthropic: if the vacuum energy assumes widely different values in different regions of the universe, then conscious observers will find themselves in regions of the universe where the vacuum energy is low enough to allow structure formation (Efstathiou 1995, Martel et al. 1998). This type of explanation finds a natural home in "multiverse" models of eternal inflation, where different histories of spontaneous symmetry breaking lead to different values of physical constants in each non-inflating "bubble" (Linde 1987), and it has gained new prominence in the context of string theory, which predicts a "landscape" of vacua arising from different compactifications of spatial dimensions (Susskind 2003). One can attempt to derive an expectation value of the observed cosmological constant from such arguments (e.g., Martel et al. 1998), but the results are sensitive to the choice of parameters that are allowed to vary (Tegmark and Rees 1998) and to the choice of measure on parameter space, so it is hard to take such "predictions" beyond a qualitative level. A variant on these ideas is that the effective value (and perhaps even the sign) of the cosmological constant varies in time, and that structure will form and observers arise during periods when its magnitude is anomalously low compared to its natural (presumably Planck-level) energy scale (Brandenberger 2002, Griest 2002).
A straightforward alternative to a cosmological constant is a field with negative pressure (and thus repulsive gravitational effect) whose energy density changes with time (Ratra and Peebles 1988, Frieman et al. 1995, Ferreira and Joyce 1997). In particular, a canonical scalar field ϕ with potential V(ϕ) has energy density and pressure
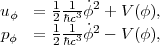 |
(1) |
so if the kinetic term is subdominant, then pϕ ≈ -uϕ. A slowly rolling scalar field of this sort is analogous to the inflaton field hypothesized to drive inflation, but at an energy scale many, many orders of magnitude lower. In general, a scalar field has an equation-of-state parameter
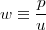 |
(2) |
that is greater than -1 and varies in time, while a true cosmological constant has w=-1 at all times. Some forms of V(ϕ) allow attractor or "tracker" solutions in which the late-time evolution of ϕ is insensitive to the initial conditions (Ratra and Peebles 1988, Steinhardt et al. 1999), and a subset of these allow uϕ to track the matter energy density at early times, ameliorating the coincidence problem (Skordis and Albrecht 2002). Some choices give a nearly constant w that is different from -1, while others have w≈ -1 as an asymptotic state at either early or late times, referred to respectively as "thawing" or "freezing" solutions (Caldwell and Linder 2005).
Scalar field models in which the energy density is dominated by V(ϕ) are popularly known as "quintessence" (Zlatev et al. 1999). A number of variations have been proposed in which the energy density of the field is dominated by kinetic, spin, or oscillatory degrees of freedom (e.g., Armendariz-Picon et al. 2001, Boyle et al. 2002). Other models introduce non-canonical kinetic terms or couple the field to dark matter. Models differ in the evolution of uϕ(a) and w(a), and some have other distinctive features such as large scale energy density fluctuations that can affect CMB anisotropies. Of course, none of these models addresses the original "cosmological constant problem" of why the true vacuum energy is unobservably small.
The alternative to introducing a new energy component is to modify General Relativity itself on cosmological scales, for example by replacing the Ricci scalar R in the gravitational action with some higher order function f(R) (e.g., Capozziello and Fang 2002, Carroll et al. 2004), or by allowing gravity to "leak" into an extra dimension in a way that reduces its attractive effect at large scales (Dvali et al. 2000). GR modifications can alter the relation between the expansion history and the growth of matter clustering, and, as discussed in subsequent sections, searching for mismatches between observational probes of expansion and observational probes of structure growth is one generic approach to seeking signatures of modified gravity. To be consistent with tight constraints from solar system tests, modifications of gravity must generally be "shielded" on small scales, by mechanisms such as the "chameleon" effect, the "symmetron" mechanism, or "Vainshtein screening" (see the review by Jain and Khoury 2010). These mechanisms can have the effect of introducing intermediate scale forces. GR modifications can also alter the relation between non-relativistic matter clustering and gravitational lensing, which in standard GR is controlled by two different potentials that are equal to each other for fluids without anisotropic stress.
The distinction between a new energy component and a modification of gravity may be ambiguous. The most obvious ambiguous case is the cosmological constant itself, which can be placed on either the "curvature" side or the "stress-energy" side of the Einstein field equation. More generally, many theories with f(R) modifications of the gravitational action can be written in a mathematically equivalent form of GR plus a scalar field with specified properties (Chiba 2003, Kunz and Sapone 2007). Relative to expectations for a cosmological constant or a simple scalar field model, models in which dark matter decays into dark energy can produce a mismatch between the histories of expansion and structure growth while maintaining GR (e.g., Jain and Zhang 2008, Wei and Zhang 2008). Thus, even perfect measurements of all relevant observables may not uniquely locate the explanation of cosmic acceleration in the gravitational or stress-energy sector.
There is a minority opinion (see Buchert 2011 for a recent review article) that the phenomena interpreted as evidence for dark energy could instead arise from the backreaction of small scale inhomogeneities on the large scale cosmic expansion. This line of argument contends that the expansion rate of a universe with small scale inhomogeneity can differ significantly from that of a homogeneous universe with the same average density. In our view, the papers on this theme present an incorrect interpretation of correct underlying equations, and we do not see these "inhomogeneous averaging" effects as a viable alternative to dark energy. Baumann et al. (2012) present a detailed counter-argument, treating inhomogeneous matter as a fluid with an effective viscosity and pressure and demonstrating that the backreaction on the evolution of background expansion and large scale perturbations is extremely small. (See Green and Wald 2011 for an alternative form of this counter-argument and Peebles 2010 for a less formal but still persuasive version.) In a somewhat related vein, the suggestion that acceleration could arise from superhorizon fluctuations generated by inflation (Barausse et al. 2005, Kolb et al. 2005) is ruled out by a complete perturbation analysis (Hirata and Seljak 2005).
While the term "dark energy" seems to presuppose a stress-energy explanation, in practice it has become a generic term for referring to the cosmic acceleration phenomenon. In particular, the phrase "dark energy experiments" has come to mean observational studies aimed at measuring acceleration and uncovering its cause, regardless of whether that cause is a new energy field or a modification of gravity. We will generally adopt this common usage of "dark energy" in this review, though where the distinction matters we will try to use "cosmic acceleration" as our generic term. It is important to keep in mind that we presently have strong observational evidence for accelerated cosmic expansion but no compelling evidence that the cause of this acceleration is really a new energy component.
The magnitude and coincidence problems are challenges for any explanation of cosmic acceleration, whether a cosmological constant, a scalar field, or a modification of GR. The coincidence problem seems like an important clue for identifying a correct solution, and some models at least reduce its severity by coupling the matter and dark energy densities in some way. Multiverse models with anthropic selection arguably offer a solution to the coincidence problem, because if the probability distribution of vacuum energy densities rises swiftly towards high values, then structure may generically form at a time when the matter and vacuum energy density values are similar, in that small subset of universes where structure forms at all. But sometimes a coincidence is just a coincidence. Essentially all current theories of cosmic acceleration have one or more adjustable parameters whose value is tuned to give the observed level of acceleration, and none of them yield this level as a "natural" expectation unless they have built it in ahead of time. These theories are designed to explain acceleration itself rather than emerging from independent theoretical considerations or experimental constraints. Conversely, a theory that provided a compelling account of the observed magnitude of acceleration — like GR's successful explanation of the precession of Mercury — would quickly jump to the top of the list of cosmic acceleration models.
The deep mystery and fundamental implications of cosmic acceleration have inspired numerous ambitious observational efforts to measure its history and, it is hoped, reveal its origin. The report of the Dark Energy Task Force (DETF; Albrecht et al. 2006) played a critical role in systematizing the field, by categorizing experimental approaches and providing a quantitative framework to compare their capabilities. The DETF categorized then-ongoing experiments as "Stage II" (following the "Stage I" discovery experiments) and the next generation as "Stage III." It looked forward to a generation of more capable (and more expensive) "Stage IV" efforts that might begin observations around the second half of the coming decade. The DETF focused on the same four methods that will be the primary focus of this review: Type Ia supernovae, baryon acoustic oscillations (BAO), weak gravitational lensing, and clusters of galaxies.
Six years on, the main "Stage II" experiments have completed their observations though not necessarily their final analyses. Prominent examples include the supernova and weak lensing programs of the CFHT Legacy Survey (CFHTLS; Conley et al. 2011, Semboloni et al. 2006a, Heymans et al. 2012b), the ESSENCE supernova survey (Wood-Vasey et al. 2007), BAO measurements from the Sloan Digital Sky Survey (SDSS; Eisenstein et al. 2005, Percival et al. 2010, Padmanabhan et al. 2012), and the SDSS-II supernova survey (Frieman et al. 2008). These have been complemented by extensive multi-wavelength studies of local and high-redshift supernovae such as the Carnegie Supernova Project (Hamuy et al. 2006, Freedman et al. 2009), by systematic searches for z > 1 supernovae with Hubble Space Telescope (Riess et al. 2007, Suzuki et al. 2012), by dark energy constraints from the evolution of X-ray or optically selected clusters (Henry et al. 2009, Mantz et al. 2010, Vikhlinin et al. 2009, Rozo et al. 2010), by improved measurements of the Hubble constant (Riess et al. 2009, Riess et al. 2011, Freedman et al. 2012), and by CMB data from the WMAP satellite (Bennett et al. 2003, Larson et al. 2011) and from ground-based experiments that probe smaller angular scales. 4 Most data remain consistent with a spatially flat universe and a cosmological constant with ΩΛ = 1 - Ωm ≈ 0.75, with an uncertainty in the equation-of-state parameter w that is roughly ± 0.1 at the 1-2σ level. Substantial further improvement will in many cases require reduction in systematic errors as well as increased statistical power from larger data sets.
The clearest examples of "Stage III" experiments, now in the late construction or early operations phase, are the Dark Energy Survey (DES), Pan-STARRS 5, the Baryon Oscillation Spectroscopic Survey (BOSS) of SDSS-III, and the Hobby-Eberly Telescope Dark Energy Experiment (HETDEX). 6 All four projects are being carried out by international, multi-institutional collaborations. Pan-STARRS and DES will both carry out large area, multi-band imaging surveys that go a factor of ten or more deeper (in flux) than the SDSS imaging survey (Abazajian et al. 2009), using, respectively, a 1.4-Gigapixel camera on the 1.8-m PS1 telescope on Haleakala in Hawaii and a 0.5-Gigapixel camera on the 4-m Blanco telescope on Cerro Tololo in Chile. These imaging surveys will be used to measure structure growth via weak lensing, to identify galaxy clusters and calibrate their masses via weak lensing, and to measure BAO in galaxy angular clustering using photometric redshifts. Each project also plans to carry out monitoring surveys over smaller areas to discover and measure thousands of Type Ia supernovae. Fully exploiting BAO requires spectroscopic redshifts, and BOSS will carry out a nearly cosmic-variance limited survey (over 104 deg2) out to z ≈ 0.7 using a 1000-fiber spectrograph to measure redshifts of 1.5 million luminous galaxies, and a pioneering quasar survey that will measure BAO at z ≈ 2.5 by using the Lyα forest along 150,000 quasar sightlines to trace the underlying matter distribution. HETDEX plans a BAO survey of 106 Lyα-emitting galaxies at z ≈ 3.
There are many other ambitious observational efforts that do not fit so neatly into the definition of a "Stage III dark energy experiment" but will nonetheless play an important role in "Stage III" constraints. A predecessor to BOSS, the WiggleZ project on the Anglo-Australian 3.9-m telescope, recently completed a spectroscopic survey of 240,000 emission line galaxies out to z = 1.0 (Blake et al. 2011a). The Hyper Suprime-Cam (HSC) facility on the Subaru telescope will have wide-area imaging capabilities comparable to DES and Pan-STARRS, and it is likely to devote substantial fractions of its time to weak lensing surveys. Other examples include intensive spectroscopic and photometric monitoring of supernova samples aimed at calibration and understanding of systematics, new HST searches for z > 1 supernovae, further improvements in H0 determination, deeper X-ray and weak lensing studies of samples of tens or hundreds of galaxy clusters, and new cluster searches via the Sunyaev and Zeldovich (1970) effect using the South Pole Telescope (SPT), the Atacama Cosmology Telescope (ACT), or the Planck satellite. In addition, Stage III analyses will draw on primary CMB constraints from Planck.
The Astro2010 report identifies cosmic acceleration as one of the most pressing questions in contemporary astrophysics, and its highest priority recommendations for new ground-based and space-based facilities both have cosmic acceleration as a primary science theme. 7 On the ground, the Large Synoptic Survey Telescope (LSST), a wide-field 8.4-m optical telescope equipped with a 3.2-Gigapixel camera, would enable deep weak lensing and optical cluster surveys over much of the sky, synoptic surveys that would detect and measure tens of thousands of supernovae, and photometric-redshift BAO surveys extending to z ≈ 3.5. BigBOSS, highlighted as an initiative that could be supported by the proposed "mid-scale innovation program," would use a highly multiplexed fiber spectrograph on the NOAO 4-m telescopes to carry out spectroscopic surveys of ~ 107 galaxies to z ≈ 1.6 and Lyα forest BAO measurements at z > 2.2. Another potential ground-based method for large volume BAO surveys is radio "intensity mapping," which seeks to trace the large scale distribution of neutral hydrogen without resolving the scale of individual galaxies. In the longer run, the Square Kilometer Array (SKA) could enable a BAO survey of ~ 109 HI-selected galaxies and weak lensing measurements of ~ 1010 star-forming galaxies using radio continuum shapes.
Space observations offer two critical advantages for cosmic acceleration studies: stable high resolution imaging over large areas, and vastly higher sensitivity at near-IR wavelengths. (For cluster studies, space observations are also the only route to X-ray measurements.) These advantages inspired the Supernova Acceleration Probe (SNAP), initially designed with a concentration on supernova measurements at 0.1 < z < 1.7, and later expanded to include a wide area weak lensing survey as a major component. Following the National Research Council's Quarks to Cosmos report (Committee On The Physics Of The Universe 2003), NASA and the U.S. Department of Energy embarked on plans for a Joint Dark Energy Mission (JDEM), which has considered a variety of mission architectures for space-based supernova, weak lensing, and BAO surveys. The Astro2010 report endorsed as its highest priority space mission a Wide Field Infrared Survey Telescope (WFIRST), which would carry out imaging and dispersive prism spectroscopy in the near-IR to support all of these methods, and, in addition, a planetary microlensing program, a Galactic plane survey, and a guest observer program. The recently completed report of the WFIRST Science Definition Team (Green et al. 2012) presents detailed designs and operational concepts, with a primary design reference mission that includes three years of dark energy programs (out of a five year mission) on an unobstructed 1.3-meter telescope with a 0.375 deg2 near-IR focal plane (150 million 0.18" pixels). The recent transfer of two 2.4-meter diameter telescopes from the U.S. National Reconnaissance Office (NRO) to NASA opens the door for a potential implementation of WFIRST on a larger platform; this possibility is now a subject of active, detailed study (see Dressler et al. 2012 for an initial assessment). WFIRST faces significant funding hurdles, despite its top billing in Astro2010, but a launch in the early 2020s still appears likely. On the European side, ESA recently selected the Euclid 8 satellite as a medium-class mission for its Cosmic Vision 2015-2025 program, with launch planned for 2020. Euclid plans to carry out optical and near-IR imaging and near-IR slitless spectroscopy over roughly 14,000 deg2, for weak lensing and BAO measurements. In its current design (Laureijs et al. 2011), Euclid utilizes a 1.2-meter telescope, a 0.56 deg2 optical focal plane (604 million 0.10" pixels), and a near-IR focal plane with similar area but larger pixels (67 million 0.30" pixels). Well ahead of either Euclid or WFIRST, the European X-ray telescope eROSITA (on the Russian Spectrum Roentgen Gamma satellite) is expected to produce an all-sky catalog of ~ 105 X-ray selected clusters, with X-ray temperature measurements and resolved profiles for the brighter clusters (Merloni et al. 2012). 9
The completion of the Astro2010 Decadal Survey and the Euclid selection by ESA make this an opportune time to review the techniques and prospects for probing cosmic acceleration with ambitious observational programs. Our goal is, in some sense, an update of the DETF report (Albrecht et al. 2006), incorporating the many developments in the field over the last few years and (the difference between a report and a review) emphasizing explanation rather than recommendation. We aim to complement other reviews of the field that differ in focus or in level of detail. To mention just a selection of these, we note that Frieman et al. (2008) and Blanchard (2010) provide excellent overviews of the field, covering theory, current observations, and future experiments, while Astier and Pain (2012) cover the observational approaches concisely; Peebles and Ratra (2003) and Copeland et al. (2006) are especially good on history of the subject and on theoretical aspects of scalar field models; Jain and Khoury (2010) review the observational and (especially) theoretical aspects of modified gravity models in much greater depth than we cover here; Carroll (2003) and Linder (2003b, 2007) provide accessible and informative introductions at the less forbidding length of conference proceedings; Linder (2010) provides a review aimed at a general scientific audience; and the conference proceedings by Peebles (2010) nicely situates the cosmic acceleration problem in the broader context of contemporary cosmology. The distinctive features of the present review are our in-depth discussion of individual observational methods and our new quantitative forecasts for how combinations of these methods can constrain parameters of cosmic acceleration theories.
To the extent that we have a consistent underlying theme, it is the importance of pursuing a balanced observational program. We do not believe that all methods or all implementations of methods are equal; some approaches have evident systematic limitations that will prevent them reaching the sub-percent accuracy level that is needed to make major contributions to the field over the next decade, while others would require prohibitively expensive investments to achieve the needed statistical precision. However, for a given level of community investment, we think there is more to be gained by doing a good job on the three or four most promising methods than by doing a perfect job on one at the expense of the others. A balanced approach offers crucial cross-checks against systematic errors, takes advantage of complementary information contained in different observables or complementary strengths in different redshift ranges, and holds the best chance of uncovering "surprises" that do not fit into the conventional categories of theoretical models. This philosophy will emerge most clearly in Section 8, where we present our quantitative forecasts. For understandable reasons, most articles and proposals (including some we have written ourselves) start from current knowledge and show the impact of adding a particular new experiment. We will instead start from a "fiducial program" that assumes ambitious but achievable advances in several different methods at once, then consider the impact of strengthening, weakening, or omitting its individual elements.
We expect that different readers will want to approach this lengthy article in different ways. For a reader who is new to the field and wants to learn it well, it makes sense to start at the beginning and read to the end. A reader interested in a specific method can skim Section 2 to get a sense of our notation, then jump to the section that describes that method (Type Ia supernovae in Section 3, BAO in Section 4, weak lensing in Section 5, and clusters in Section 6). We think that these sections will provide useful insights even to experts in the field. Section 7 provides a brief overview of emerging methods that could play an important role in future studies. Readers interested mainly in the ways that different methods contribute to constraints on cosmic acceleration models and the quantitative forecasts for Stage III and Stage IV programs can jump directly to Section 8. Finally, Section 9 provides a summary of our findings and their implications for experimental programs, and some readers may choose to start from the end (we recommend including 8.6 and 8.7 as well as Section 9), then work backwards to the supporting details.
1 Several recent papers have addressed the contributions of Lemantre, Friedmann, and Slipher to this discovery; the story is interestingly tangled (see, e.g., Block 2011, van den Bergh 2011, Livio 2011, Belenkiy 2012, Peacock 2013). Back.
2 Many of the relevant observational references will appear in subsequent sections on specific topics. Back.
3 This interpretation of the cosmological constant in the context of quantum field theory, originally due to Wolfgang Pauli, was revived in the late 1960s by Zel'dovich (1968). For further discussion of the history see Peebles and Ratra (2003). For a detailed discussion in the context of contemporary particle theory, see the review by Martin (2012). Back.
4 We follow the convention in the astronomical literature of italicizing the names and acronyms of space missions but not of ground-based facilities. For reference, note that the many acronyms that appear in the article are all defined in Appendix A, the glossary of acronyms and facilities. Back.
5 Pan-STARRS, the Panoramic Survey Telescope and Rapid Response System, is the acronym of the facility rather than the project, but cosmological surveys are among its major goals. Pan-STARRS eventually hopes to use four coordinated telescopes, but the surveys currently underway (and now nearing completion) use the first of these telescopes, referred to as PS1. Back.
6 The acronym and facilities glossary gives references to web sites and/or publications that describe these and other experiments. Back.
7 We will use the term "Astro2010 report" to refer collectively to New Worlds, New Horizons and to the panel reports that supported it. In particular, detailed discussion of these science themes and related facilities can be found in the individual reports of the Cosmology and Fundamental Physics (CFP) Science Frontiers Panel and the Electromagnetic Observations from Space (EOS), Optical and Infrared Astronomy from the Ground (OIR), and Radio, Millimeter, and Sub-Millimeter Astronomy from the Ground (RMS) Program Prioritization Panels. Information on all of these reports can be found at http://sites.nationalacademies.org/bpa/BPA_049810. Back.
9 More detailed description of Euclid and WFIRST can be found in Section 5.9, and of eROSITA in Section 6.5. Back. Back.